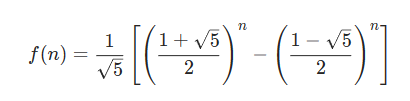文章目录
- 【LeetCode热题100】打卡第21天:最小路径和&爬楼梯
- ⛅前言
- 最小路径和
- 🔒题目
- 爬楼梯
- 🔒题目
- 🔑题解
【LeetCode热题100】打卡第21天:最小路径和&爬楼梯
⛅前言
大家好,我是知识汲取者,欢迎来到我的LeetCode热题100刷题专栏!
精选 100 道力扣(LeetCode)上最热门的题目,适合初识算法与数据结构的新手和想要在短时间内高效提升的人,熟练掌握这 100 道题,你就已经具备了在代码世界通行的基本能力。在此专栏中,我们将会涵盖各种类型的算法题目,包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等,并会提供详细的解题思路以及Java代码实现。如果你也想刷题,不断提升自己,就请加入我们吧!QQ群号:827302436。我们共同监督打卡,一起学习,一起进步。
LeetCode热题100专栏🚀:LeetCode热题100
Gitee地址📁:知识汲取者 (aghp) - Gitee.com
题目来源📢:LeetCode 热题 100 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
PS:作者水平有限,如有错误或描述不当的地方,恳请及时告诉作者,作者将不胜感激
最小路径和
🔒题目
原题链接:64.最小路径和

-
解法一:动态规划
题目分析:①辨别题目的类型。通过阅读并辨别(这个需要学习并做过动态规划这类题型的经验,本体比较好辩别),我们可以发现这是一个典型的动态规划问题,可以使用一个db数组缓存当前节点的最短距离,然后下一个节点就可以复用,而不需要重新去计算。②思考对应的解法。既然我们已经知道,这是一个动态规划问题,剩下的就是推导出转移方程。当前节点的状态,有两个来源,要么从上边来,要么从左边来,因为是最小路径,所以我们使用 M a t h . m i n ( d b [ i − 1 ] [ j ] , d b [ i ] [ j − 1 ] ) Math.min(db[i - 1][j], db[i][j - 1]) Math.min(db[i−1][j],db[i][j−1])判断当前节点的来源,其次还需要加上当前节点的距离,最终是 d b [ i ] [ j ] = g r i d [ i − 1 ] [ j − 1 ] + M a t h . m i n ( d b [ i − 1 ] [ j ] , d b [ i ] [ j − 1 ] ) db[i][j] = grid[i - 1][j - 1] + Math.min(db[i - 1][j], db[i][j - 1]) db[i][j]=grid[i−1][j−1]+Math.min(db[i−1][j],db[i][j−1])。③完善逻辑。通过②可以得到了通用节点的转移方程,但是对于
i==1或j==1这两种情况,我们需要单独考虑,因为他们有边界,上边和左边没有元素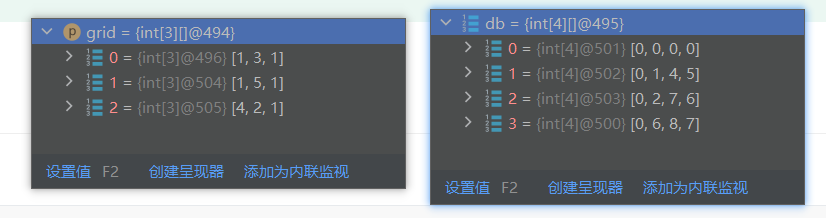
/** * @author ghp * @title 不同路径 */ class Solution { public int minPathSum(int[][] grid) { int m = grid.length; int n = grid[0].length; int[][] db = new int[m + 1][n + 1]; for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { if (i == 1 || j == 1) { db[i][j] = grid[i - 1][j - 1] + Math.max(db[i - 1][j], db[i][j - 1]); } else { db[i][j] = grid[i - 1][j - 1] + Math.min(db[i - 1][j], db[i][j - 1]); } } } return db[m][n]; } }复杂度分析
时间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
空间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
-
解法二:DFS+记忆搜索
首先最短路径问题,肯定是可以使用DFS和BFS的,但是直接暴力DFS或BFS是肯定行不通的,这里需要使用记忆搜搜。所谓的记忆搜索很简单,就是在搜索的过程中缓存当前搜索的结果,这样就能减少很多重复性的搜索,从而大大提高搜索效率
import java.util.Arrays; /** * @author ghp * @title 不同路径 */ class Solution { public int minPathSum(int[][] grid) { int m = grid.length; int n = grid[0].length; int[][] path = new int[m][n]; // 初始化path数组 for (int i = 0; i < path.length; i++) { Arrays.fill(path[i], -1); } path[m - 1][n - 1] = grid[m - 1][n - 1]; return dfs(grid, path, 0, 0); } /** * 深度搜索 * * @param grid 待搜索的图 * @param path 用于记录当前每次搜索的最短路径 * @param r 行 * @param c 列 * @return (0,0)到 (m-1,n-1) 的最短路径 */ private int dfs(int[][] grid, int[][] path, int r, int c) { if (r >= grid.length || c >= grid[0].length) { // 越界 return Integer.MAX_VALUE; } if (path[r][c] != -1) { // 该点已经走过,直接返回当前点到达终点的最短路径 return path[r][c]; } // 往下 int down = dfs(grid, path, r + 1, c); // 往右 int right = dfs(grid, path, r, c + 1); // 记录当前节点到达终点的最短路径(核心步骤) path[r][c] = grid[r][c] + Math.min(right, down); return path[r][c]; } }复杂度分析
时间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
空间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
-
解法三:BFS+记忆搜索
import java.util.Arrays; import java.util.LinkedList; import java.util.Queue; /** * @author ghp * @title 不同路径 */ class Solution { public int minPathSum(int[][] grid) { int[][] path = new int[grid.length][grid[0].length]; // 初始化记忆数组 for (int[] row : path) { Arrays.fill(row, -1); } path[0][0] = grid[0][0]; return bfs(path, grid); } private static int bfs(int[][] path, int[][] grid) { int m = grid.length; int n = grid[0].length; Queue<int[]> queue = new LinkedList<>(); queue.offer(new int[]{0, 0}); // 出发点 // 方向向量,向左,向下 int[][] dirs = {{0, 1}, {1, 0}}; // 开始进行广度搜索 while (!queue.isEmpty()) { int[] curr = queue.poll(); int x = curr[0]; int y = curr[1]; // 遍历向左和向下的点 for (int[] dir : dirs) { int dx = x + dir[0]; int dy = y + dir[1]; if (dx >= 0 && dx < m && dy >= 0 && dy < n) { // 当前没有发生越界 if (path[dx][dy] == -1 || path[dx][dy] > path[x][y] + grid[dx][dy]) { // 当前点没有被遍历 或 当前路径长度比之前路径更短,都需要更新最短路径 path[dx][dy] = path[x][y] + grid[dx][dy]; // 将当前所在坐标加入到队列中,方便遍历下一个节点 queue.offer(new int[]{dx, dy}); } } } } return path[m - 1][n - 1]; } }复杂度分析
时间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
空间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
PS:通过提交检测,可以发现虽然三者的时间复杂度和空间复杂度都是一样的,但是时间上和空间上最优的是动态规划,其次是DFS,最好才是BFS。实现起来最复杂的是BFS,其次是DFS,最后才是动态规划,所以综上所述,本题的最优解是动态规划,LeetCode官方也只提供了动态规划的题解(●ˇ∀ˇ●)
爬楼梯
🔒题目
原题链接:70.爬楼梯
🔑题解
-
解法一:暴力DFS(示例数据为44时时间超限)
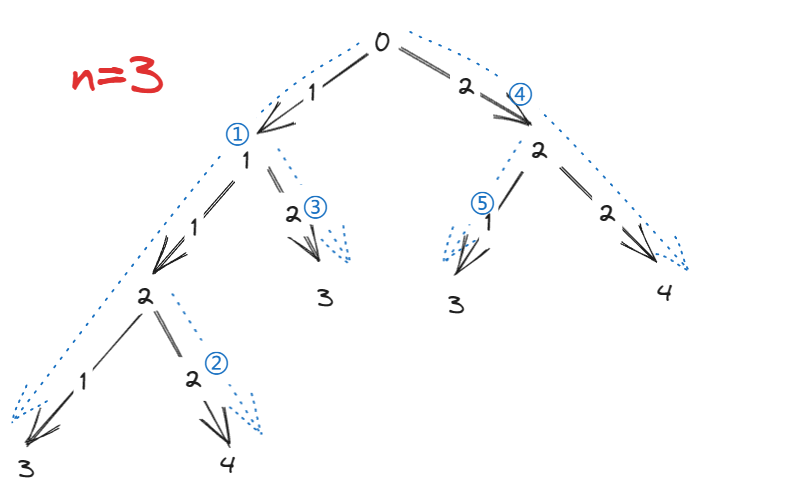
/** * @author ghp * @title 爬楼梯 */ class Solution { private int count = 0; public int climbStairs(int n) { dfs(n, 0); return count; } private void dfs(int n, int path) { if (path == n){ count++; return; } if (path > n){ return; } for (int i = 1; i <= 2; i++) { dfs(n, path+i); } } }复杂度分析:
- 时间复杂度: O ( 2 n ) O(2^n) O(2n)
- 空间复杂度: O ( n ) O(n) O(n)
代码优化:DFS+记忆搜索
可以使用记忆化搜索来优化这段代码,避免重复计算。具体实现如下:
- 创建一个记忆数组 memo,将每个位置初始化为 -1,表示没有计算过。
- 在 dfs 函数中,首先判断 memo 数组中当前状态是否计算过,若已计算过则直接返回对应的值。
- 如果 memo 数组中当前状态未计算过,则进行正常的搜索,并在结束搜索后将结果保存到 memo 数组中。
- 最后返回结果即可。
主要思想,因为DFS搜索的结果是一颗二叉树,二叉树具有对称性,当我们在左边搜索过结果,右侧搜索到同样的结果时,可以直接不需要计算,直接使用之前的计算结果
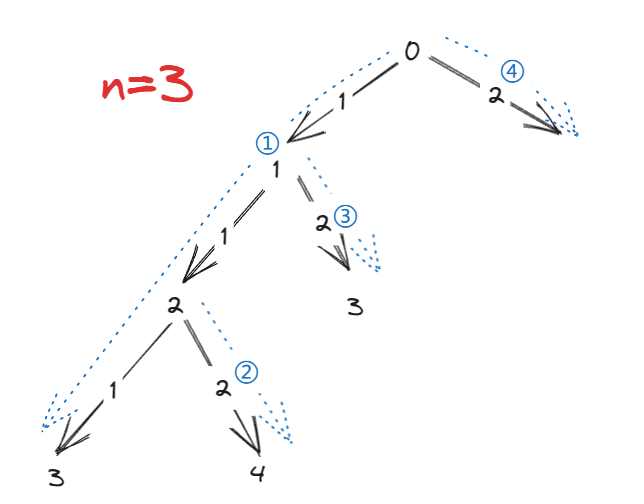
import java.util.Arrays; /** * @author ghp * @title 爬楼梯 */ class Solution { private int count = 0; // 记录可达的路径条数 private int[] memo; // 记录当前节点可达的路径条数 public int climbStairs(int n) { memo = new int[n + 1]; Arrays.fill(memo, -1); dfs(n, 0); return count; } private void dfs(int n, int path) { if (path == n) { // 当前路径符合,路径条数+1 count++; return; } if (path > n) { // 已经到底了,无法继续往下遍历 return; } if (memo[path] != -1) { // 当前节点被遍历过,则不需要继续往下遍历 count += memo[path]; return; } // 遍历当前节点下的左右子树 for (int i = 1; i <= 2; i++) { dfs(n, path + i); } // 将当前节点可达的路径总数保存到 memo 数组中 memo[path] = count; } }复杂度分析:
时间复杂度和空间复杂度和之前是一样的,通过存储每次搜索的状态,我们可以减少很多重复的搜索
-
解法二:动态规划
每一个阶梯都有两个状态,要么来自上一个(走一步),要么来自上上一个(走两步),所以我们可以得到状态转移方程: f ( x ) = f ( x − 1 ) + f ( x − 2 ) f(x)=f(x-1)+f(x-2) f(x)=f(x−1)+f(x−2),通过枚举,可以发现 f ( 1 ) = 1 , f ( 2 ) = 2 , f ( 3 ) = 3 , f ( 4 ) = 5... f(1)=1,f(2)=2,f(3)=3,f(4)=5... f(1)=1,f(2)=2,f(3)=3,f(4)=5...显然,这是一个斐波那契数列!
class Solution { public int climbStairs(int n) { int p = 0, q = 0, r = 1; for (int i = 1; i <= n; ++i) { p = q; q = r; r = p + q; } return r; } }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
-
解法三:公式法