大学物理（上）-期末知识点结合习题复习（5）——刚体力学-转动惯量、力矩、线密度面密度体密度、平行轴定理和垂直轴定理、角动量定理和角动量守恒定律

news2024/11/26 12:31:32

刚体的定轴转动

题1

题目描述

题解

题2

题解

题3

题目描述

题解

题4

题目描述

题解

题5

题目描述

题解

角动量定理和角动量守恒定律

刚体的定轴转动

1.转动动能

$E_k=\sum_{i}^{}\frac{1}{2}\Delta m_iv_i^2$

由 $v=\omega r$ ，得

$E_k=\frac{1}{2}(\sum_{i}^{}\Delta m_ir_i^2)\omega ^2$

$\Delta m_i$ 表示质量

$r_i$ 表示质量分布点

2.转动惯量

$I=\sum_{i}^{}\Delta m_ir_i^2$

$I$ 为刚体对给定轴的转动惯量，用于描述转动的惯性的大小。

所以转动动能可以表示为： $E_k=\frac{1}{2}I\omega ^2$

3.力矩

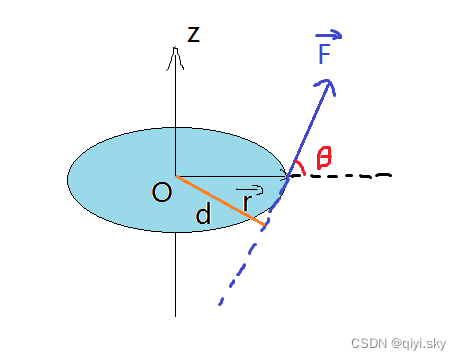
力矩（ $\overrightarrow{M}$ ）：用来描述力对刚体的转动作用的物理量。

$\overrightarrow{F}$ 对转轴z的定义： $\overrightarrow{M}=\overrightarrow{r}\times\overrightarrow{F}$

$\overrightarrow{r}$ 叉乘 $\overrightarrow{F}$ ，大小等于r的大小乘以F的大小再乘以二者夹角的正弦值，

即， $M=Fr\sin \theta =Fd$ ，d为力臂，当 $\overrightarrow{r}$ 与 $\overrightarrow{F}$ 的夹角为90度时，力矩就变成了中学时熟悉的力臂乘以力了。

方向：符合右手螺旋定则

注意：（1）若力 $\overrightarrow{F}$ 不在转动平面内，可将力分解为平行（ $\overrightarrow{F_z}$ ）和垂直（ $\overrightarrow{F_\perp }$ ）于转轴方向的两个分量。

$\overrightarrow{F}=\overrightarrow{F_z}+\overrightarrow{F_\perp }$ ，其中， $\overrightarrow{F_z}$ 对转轴的力矩为零，所以 $\overrightarrow{M}=rF_\perp \sin \theta$

（2）合力矩等于各分力矩的矢量和。

（3）刚体内作用力和反作用力的力矩相互抵消。

4.刚体的转动惯量

$I=\sum_{j}^{}\Delta m_jr_j^2$

$I=\int r^2dm$

5.线密度面密度体密度

线密度： $\lambda =\frac{m}{l}\: \: \: dm=\lambda dl$

面密度： $\sigma =\frac{m}{S}\: \: \: dm=\sigma dS$

体密度： $\rho =\frac{m}{V}\: \: \: dm=\rho dV$

6.平行轴定理和垂直轴定理

平行轴定理： $I_o=I_c+md^2$ ，d为这两轴的距离。

垂直轴定理： $I_z=I_x+I_y$

题1

题目描述

有一匀杆质量为m，长度为l，其绕O轴转动，求：对O轴的转动惯量。

题解

根据转动惯量的定义，再结合题目，我们就可以得到： $I_o=\int x^2dm$

其中x是我们已知的，杆的最大长度l就等于x；而质量dm就需要我们求一下。

根据线密度的概念： $\lambda =\frac{m}{l}$ ，那么dm就应该等于单位长度的质量乘以长度，即 $dm=\lambda dx$

所以就可以将上面的积分式写成： $I_o=\int_{0}^{l} x^2dx\lambda$

解得， $I_o=\frac{\lambda l^3}{3}$ （这个时候x就用l表示）

即得到了我们熟悉的式子， $I_o=\frac{1}{3}ml^2$ （将 $\lambda =\frac{m}{l}$ 代进去）

题2

有一匀杆质量为m，长度为l，其绕C轴转动，求：对C轴的转动惯量。

题解

与题1类似，只需要更加积分的上下限即可：

$\begin{matrix} I_c &= &\int x^2dm=\int_{-\frac{l}{2}}^{\frac{l}{2}}x^2dx\lambda \\ &= &\frac{1}{12}\lambda l^3=\frac{1}{12}ml^2\end{matrix}$

题3

题目描述

一均匀薄圆环绕O轴转动，质量为m，半径为R，线密度为 $\lambda =\frac{m}{2\pi R}$ ，求：对O轴的转动惯量。

题解

$dl$ 部分的质量为： $dm=\lambda dl$

先由转动惯量的定义得 $I_o=\int r^2dm$

代入题目中的数值变量： $I_o=\int_{0}^{2\pi R}R^2\lambda dl$

线密度和半径都为常量，提到积分前 $I_o=\lambda R^2\int_{0}^{2\pi R}dl$

解得： $I_o=\lambda R^2\cdot 2\pi R$

代入线密度 $\lambda =\frac{m}{2\pi R}$ ，也就得到了熟悉的式子： $I=mR^2$

题4

题目描述

匀质细棒长度为 $l$ ，质量为 $m$ ，绕图示 $Oy$ 轴（ $Oy$ 垂直棒）转动的转动惯量等于？

题解

将题目画成这样：

我们知道如果绕 $Oz$ 轴转动的话，其转动惯量为 $\frac{1}{12}ml^2$ 。

发现两轴平行，相距距离为 $\frac{1}{4}l$ ，那么就可以利用平行轴定理来求这道题的转动惯量了。

$I=I_z+md^2=\frac{1}{12}ml^2+m(\frac{1}{4}l)^2=\frac{7}{48}ml^2$

题5

题目描述

已知圆盘 $I_z=\frac{1}{2}mR^2$ ，求对圆盘的一条直径的 $I_x$ 或 $I_y$ .

题解

这道题运用垂直轴定理， $I_z=I_x+I_y$ .

因为圆盘中任意直径的转动惯量一致，所以 $I_x=I_y$

又 $I_z=\frac{1}{2}mR^2$

联立上面式子可得： $I_x=I_y=\frac{1}{4}mR^2$

角动量定理和角动量守恒定律

7.质点的角动量

$\overrightarrow{L}=\overrightarrow{r}\times\overrightarrow{P}=\overrightarrow{r}\times m\overrightarrow{v}$

大小： $L=rmv\sin \theta$

方向：符合右手螺旋定则

8.质点的角动量定理

$\frac{d\overrightarrow{L}}{dt}=\overrightarrow{r}\times\overrightarrow{F}$ （微分形式）

$\overrightarrow{L_2}-\overrightarrow{L_1}=\int_{t_1}^{t_2}(\overrightarrow{r}\times\overrightarrow{F})dt$ （积分形式）

因为力矩 $\overrightarrow{M}=\overrightarrow{r}\times\overrightarrow{F}$

所以，

角动量定理： 质点对于给定参考点的角动量随时间的变化率等于质点所受合外力对同一参考点O的力矩。

$\overrightarrow{M}=\frac{d\overrightarrow{L}}{dt}\: \: \: \:$

$\int_{t_1}^{t_2}\overrightarrow{M}dt=\overrightarrow{L_2}-\overrightarrow{L_1}$

9.质点的角动量守恒定律

若 $\overrightarrow{M}=0$ ，则 $\frac{d\overrightarrow{L}}{dt}=0$ ，即 $\overrightarrow{L}=$ 常矢量。

因为 $\overrightarrow{M}=\overrightarrow{r}\times\overrightarrow{F}$ ，所以可以是三种情况：1. $\overrightarrow{r}=0$ ，2. $\overrightarrow{F}=0$ ，3. $\overrightarrow{r}$ 与 $\overrightarrow{F}$ 同向或反向。

注意：角动量和力矩都是对选定的同一参考点得到的，所以角动量守恒定律只对选定的参考点才有意义。

10.刚体定轴转动的角动量

$\overrightarrow{L}=\sum_{i}^{}m_ir_i^2\overrightarrow{\omega }$

$\overrightarrow{L}=I\overrightarrow{\omega }$

11.刚体定轴转动的角动量定理

$\overrightarrow{M}=\frac{d(\overrightarrow{I\omega })}{dt}=\frac{d\overrightarrow{L}}{dt}$

$\overrightarrow{M}dt=d\overrightarrow{L}$

$\int_{t_1}^{t_2}Mdt=I\omega _2-I\omega _1$

12.刚体定轴转动的角动量守恒定律

若 $\overrightarrow{M}=0$ ，则 $L=I\omega =$ 常量

角动量守恒定律：

如果物体所受的合外力矩等于零，或者不受外力矩的作用，物体的角动量保持不变。

注意：

（1）守恒条件： $\overrightarrow{M}=0$ （合外力矩）若 $I$ 不变， $\omega$ 也不变；若 $I$ 变， $\omega$ 也变，但 $L=I\omega$ 不变。

（2）内力矩不改变系统的角动量。

（3）在冲击等问题中， $\because M^{in}\gg M^{ex} \: \: \: \: \: \therefore L\approx$ 常量。

（4）角动量守恒定律是自然界的一个基本定律。

end

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/643640.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

大学物理（上）-期末知识点结合习题复习（5）——刚体力学-转动惯量、力矩、线密度面密度体密度、平行轴定理和垂直轴定理、角动量定理和角动量守恒定律

刚体的定轴转动

题1

题目描述

题解

题2

题解

题3

题目描述

题解

题4

题目描述

题解

题5

题目描述

题解

角动量定理和角动量守恒定律

相关文章

原生小程序微信小程序使用ucharts

2023互联网寒冬之下Java程序员要怎么应对才能找到工作

Gin框架原生方式切割日志，Go语言原生日志切割

DAY21——二叉树part7

【Java算法题】剑指offer_数据结构之03队列栈

django的项目结构介绍

面向对象的多态

作为软件工程师对Docker的认知和看法

k8s如何使用ceph rbd块存储（静态供给、存储类动态供给）

mysql 最常用的一些语句

Stimulsoft Forms.WEB 23.2.6 Crack

英伟达开发板学习系列---国产【Jetson Xavier NX】系统安装及基础配置

Redis GEO地理位置信息的应用

湖南大学CS-2020期末考试解析

湖南大学CS-2018期末考试解析

湖南大学CS-2017（另一张）期末考试解析

八大排序算法之归并排序(递归实现+非递归实现)

C:\Users\BC＞conda -V ‘conda‘ 不是内部或外部命令，也不是可运行的程序或批处理文件。

css属性计算过程

丢失d3dcompiler47.dll怎么办，这个五个修复方法都可以解决

大学物理（上）-期末知识点结合习题复习（5）——刚体力学-转动惯量、力矩、线密度 面密度 体密度、平行轴定理和垂直轴定理、角动量定理和角动量守恒定律

刚体的定轴转动

题1

题目描述

题解

题2

题解

题3

题目描述

题解

题4

题目描述

题解

题5

题目描述

题解

角动量定理和角动量守恒定律

相关文章

大学物理（上）-期末知识点结合习题复习（5）——刚体力学-转动惯量、力矩、线密度面密度体密度、平行轴定理和垂直轴定理、角动量定理和角动量守恒定律