一.归并排序的基本思想

归并排序是基于分治思想和归并操作而设计出来的一种高效排序算法
所谓的归并操作就是将两个有序的子序列合并为一个有序序列的操作(归并操作算法的时间复杂度为O(N+M),N+M分别为两个子数组的元素个数)

归并排序算法思想(排升序为例)

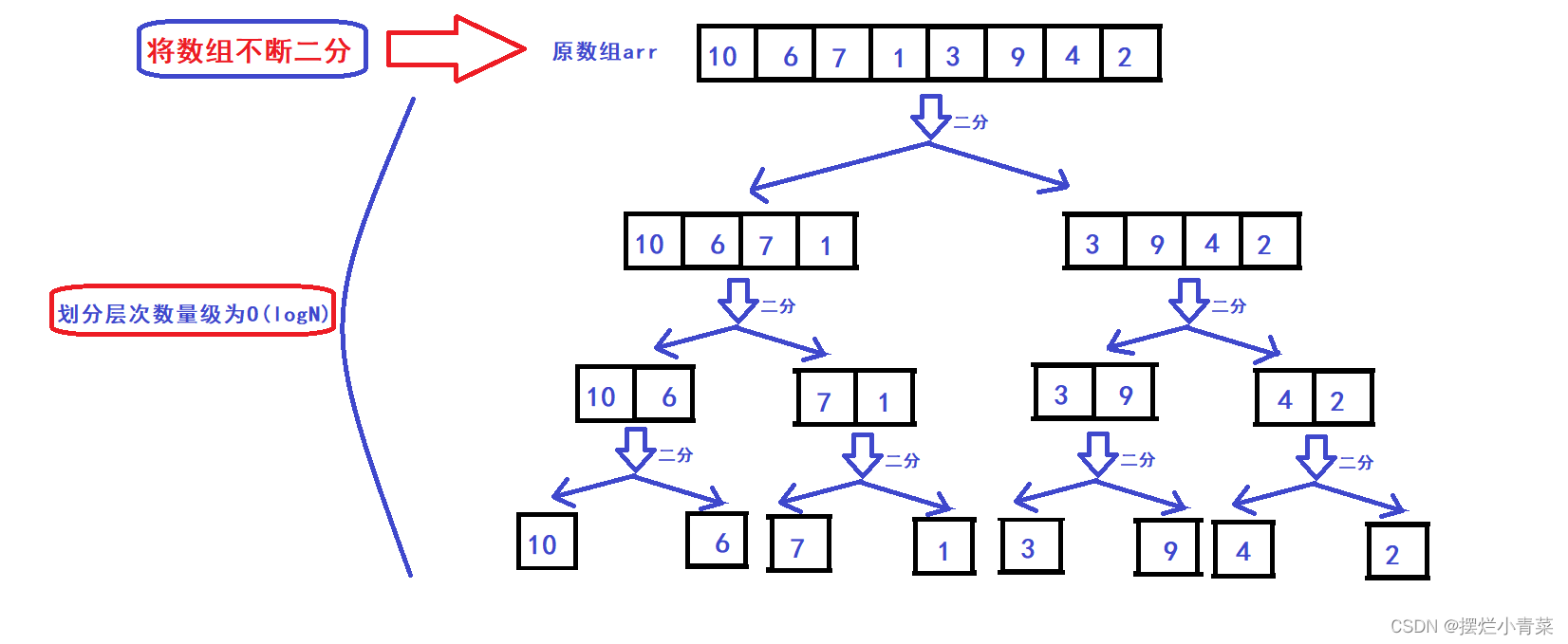
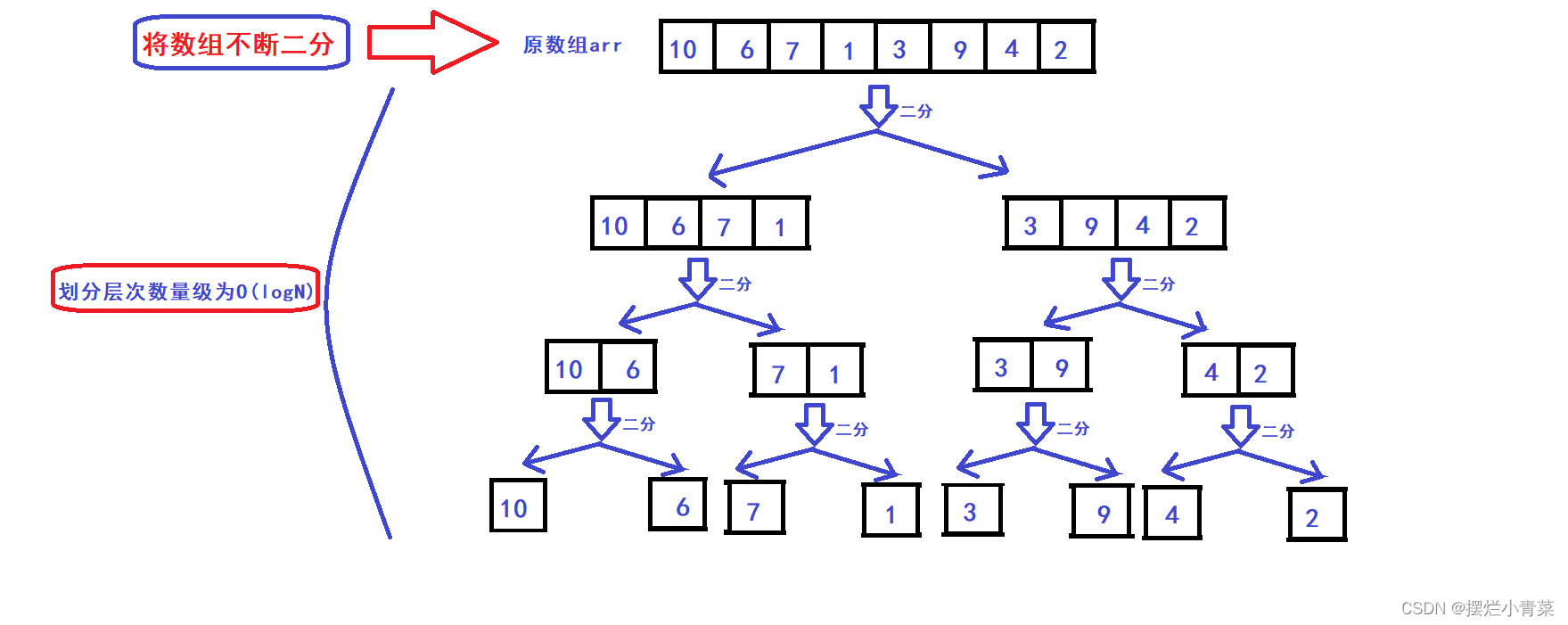
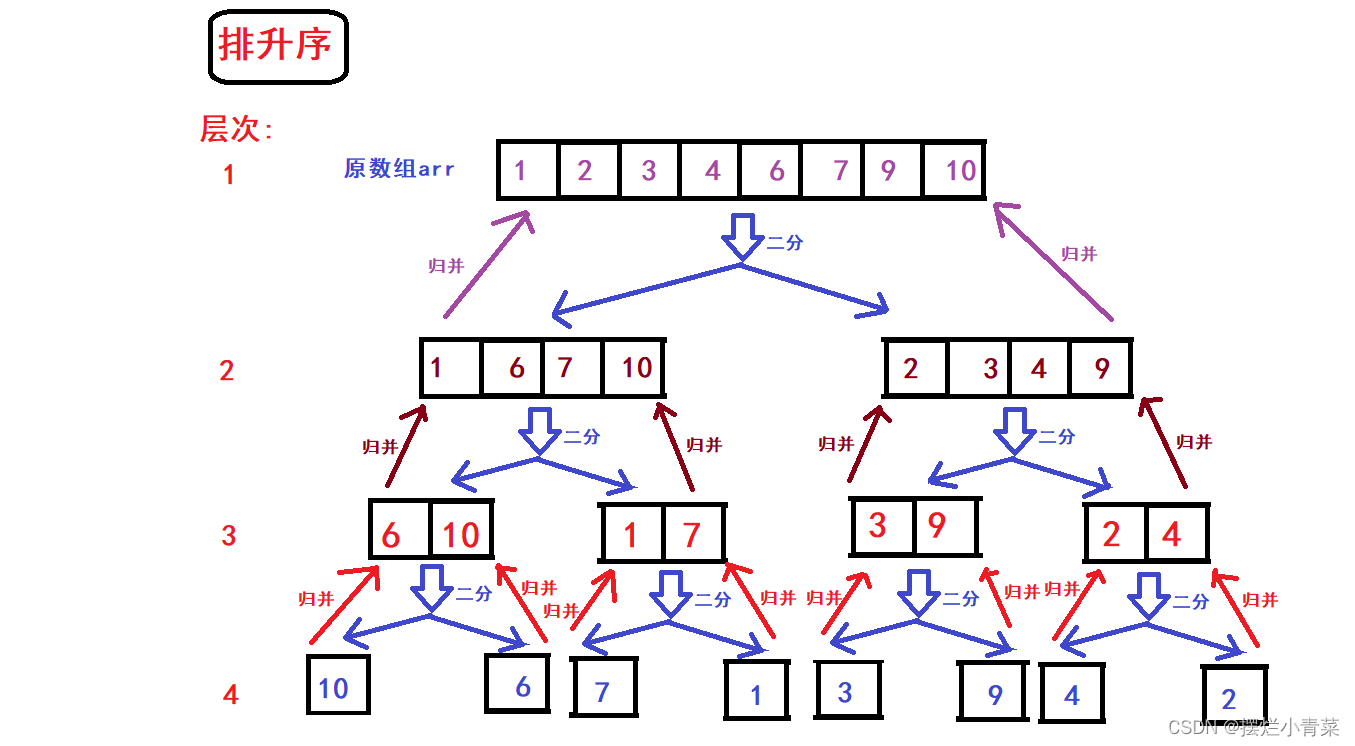
假设数组有N个元素,先将数组不断地二分,直到将数组划分为N个由单个元素构成的子数组,整个划分过程中所有子数组构成满二叉树(或接近满二叉树)的逻辑结构,如图:
数组划分完后再逐层向上将二叉树兄弟结点子数组(具有相同前驱结构)两两进行归并操作完成排序:
归并操作算法的时间复杂度为O(M1+M2),M1+M2分别为两个子数组的元素个数,因此二叉树一层子数组的两两归并操作的总时间复杂度为O(N)(N表示原数组的元素个数),而满二叉树的层次数量级为O(logN),因此归并排序的总体时间复杂度为O(NlogN)
由于归并排序的数组划分每次都是严格地二分,因此每次排序(无论具体面对怎样的序列)子数组划分结构都是稳定的满二叉树(或接近满二叉树)结构,因此归并排序的时间复杂度在各种情况下都不会有变化(不会像快排,希尔排那样由于所处理的序列的逆序数的差异而导致算法时间复杂度有所变化)
然而由于有序序列归并操作需要额外开辟数组来完成,因此归并排序有较大的空间消耗,这是归并排序的一个缺陷

二.两个有序子序列(同一个数组中)的归并(排升序)

函数首部:
void MergeSort(int* arr,int* tem, int left,int right)
arr是被分割的原数组,tem是用于归并操作的临时数组,left是arr的左端下标,right是arr的右端下标

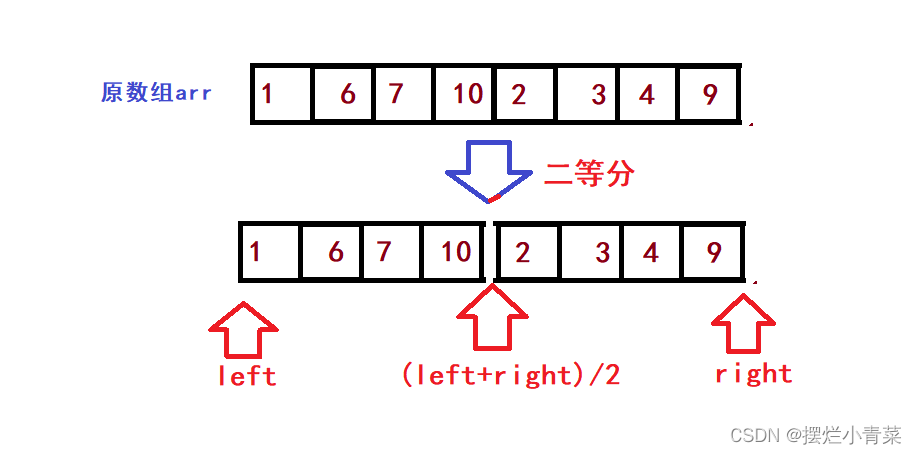
假设数组arr被二等分为两个子序列(两个子序列都是有序的):
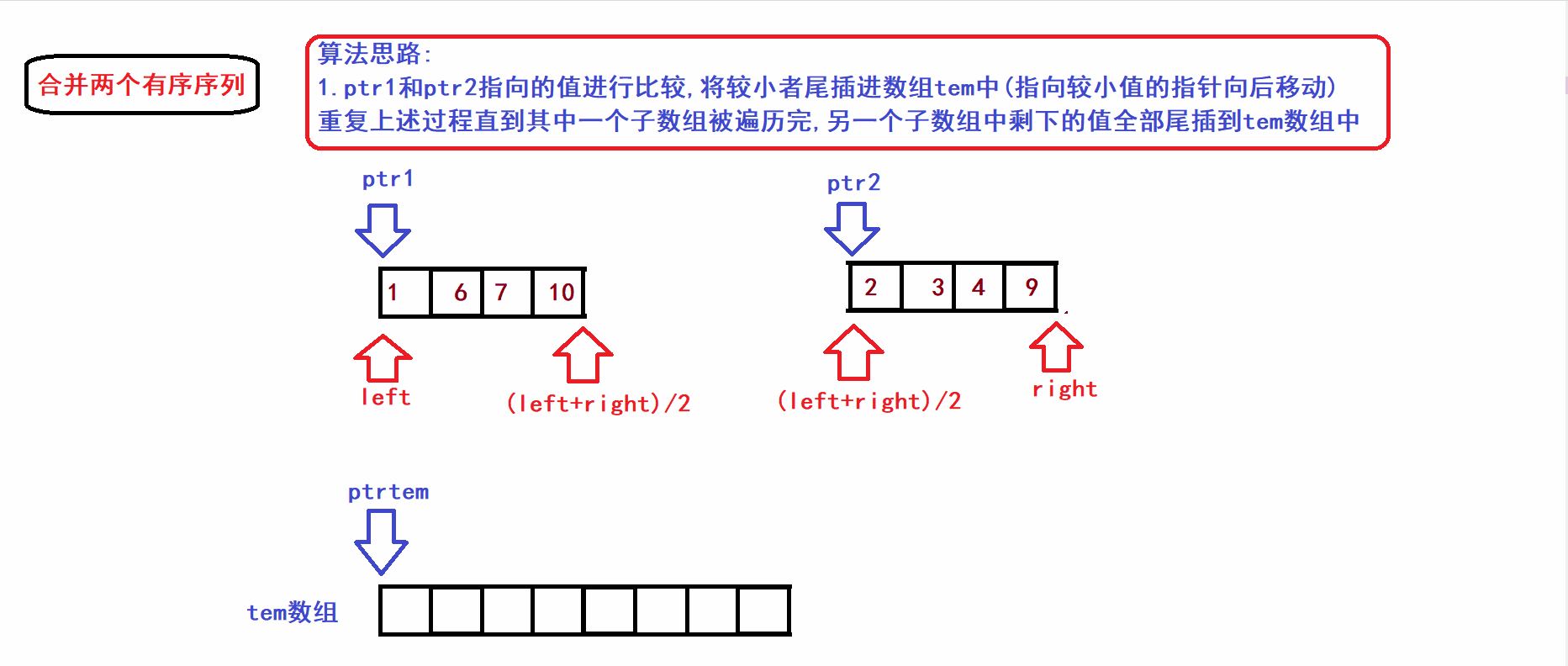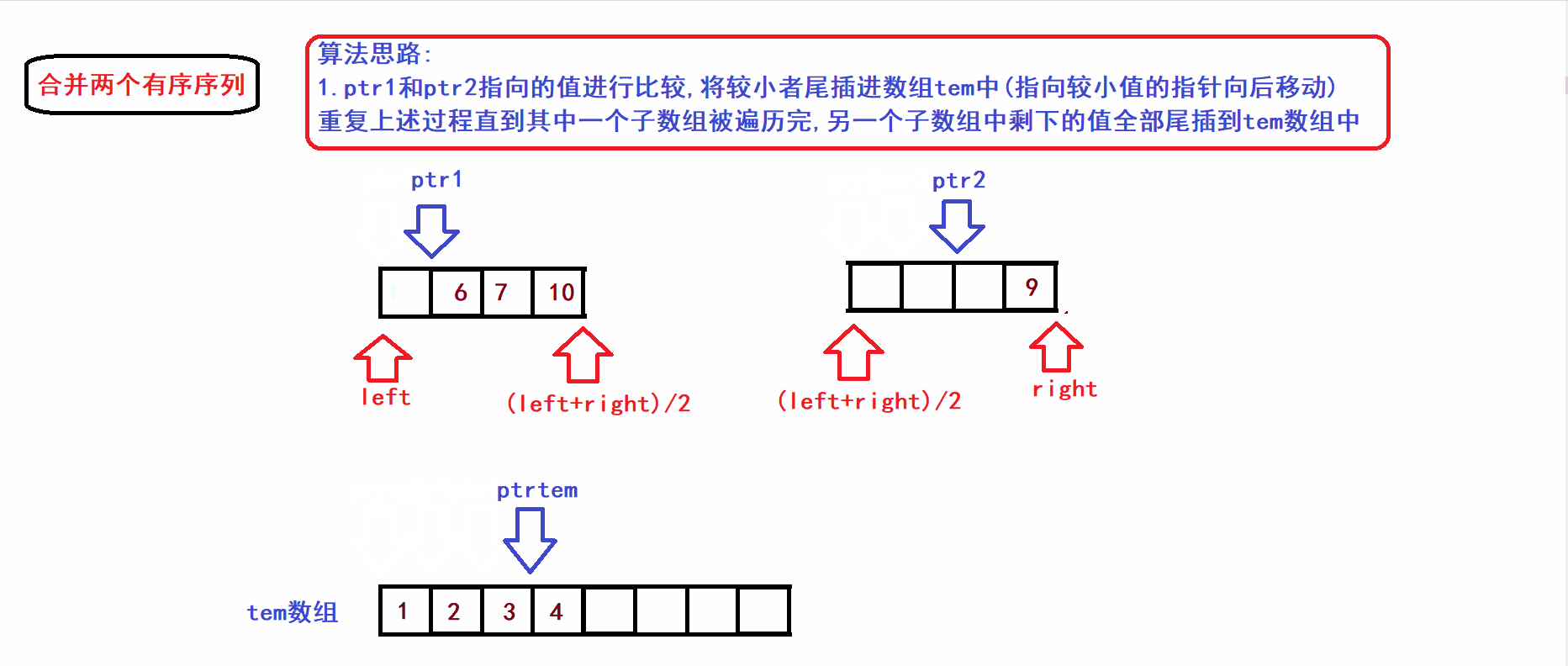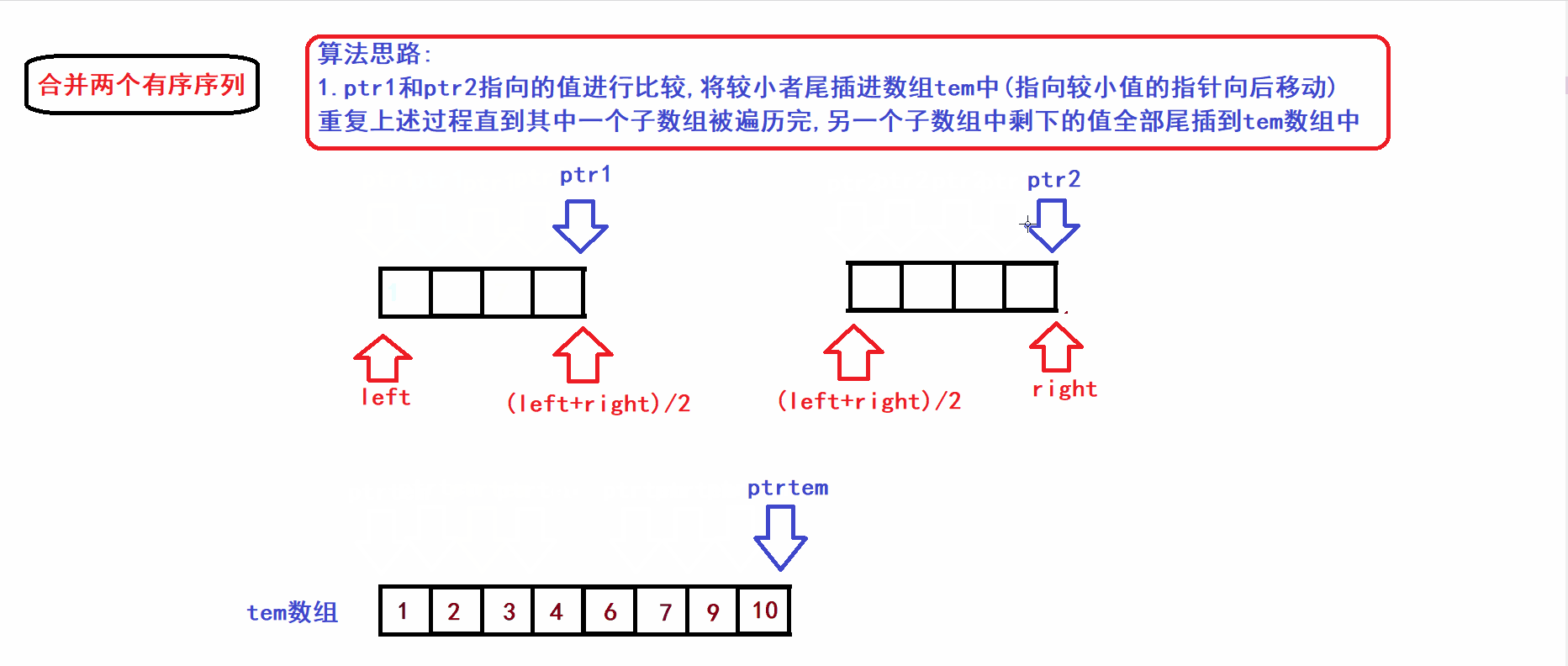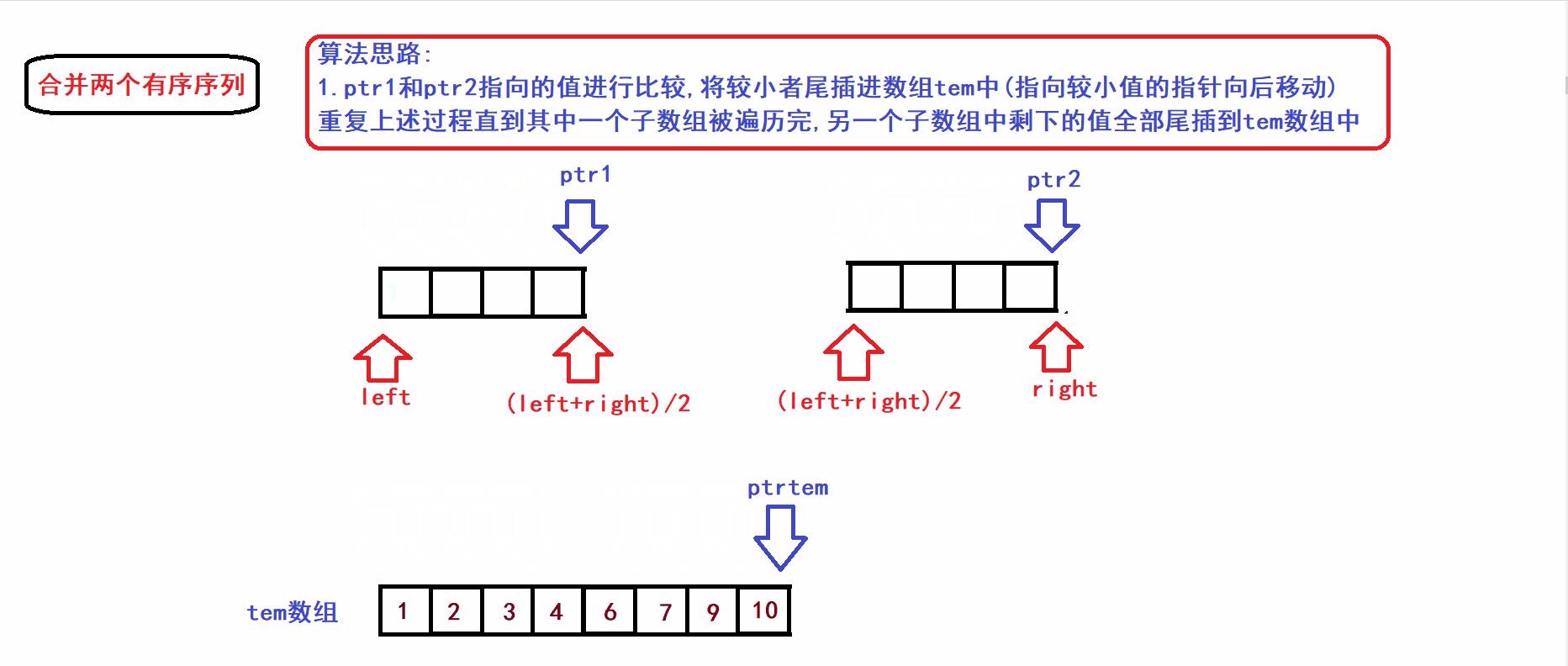
接下来我们将上图中的[left,(left+right)/2)和[(left+right)/2),right)两个子序列(有序)合并到一个tem数组中构成一个新的有序序列(利用三指针操作完成归并):
从算法gif中不难看出,归并操作的时间复杂度与两个子数组的元素个数成线性关系

两个有序序列归并操作代码:
void MergeSort(int* arr,int* tem, int left,int right)
{
	int mid = left + (right - left) / 2;			//找到数组[left,right]的中间分割点

	int ptr1 = left;								//ptr1指向左子数组的首元素
	int ptr2 = mid;									//ptr2指向右子数组的首元素
	int ptrtem = left;                              //ptrtem用于在tem数组中尾插数据
	while (ptr1 < mid && ptr2 < right)				//ptr1和ptr2其中一个遍历完子数组就停止循环
	{
		//将较小元素尾插进tem数组中
		if (arr[ptr1] > arr[ptr2])
		{
			tem[ptrtem] = arr[ptr2];
			++ptrtem;
			++ptr2;
		}
		else
		{
			tem[ptrtem] = arr[ptr1];
			++ptrtem;
			++ptr1;
		}
	}
	//将未被遍历完的子数组剩下的元素尾插到tem数组中
	while (ptr1 < mid)
	{
		tem[ptrtem] = arr[ptr1];
		++ptrtem;
		++ptr1;
	}
	while (ptr2 < right)
	{
		tem[ptrtem] = arr[ptr2];
		++ptrtem;
		++ptr2;
	}
	
	//将归并好的有序序列拷贝到原数组arr上
	for (int i = left; i < right; ++i)
	{
		arr[i] = tem[i];
	}
}

三.归并排序的递归实现

递归函数首部:
void MergeSort(int* arr,int* tem, int left,int right)
arr是被分割的原数组,tem是用于归并操作的临时数组,left是arr的子数组的左端下标,right是arr的子数组的右端下标
在进行子数组两两归并之前,我们先要进行数组的二分分治:
我们可以通过分治递归来完成数组的整个二分过程(每个子数组的区间端点下标都被存储在递归函数的各函数栈帧中):(数组二分的递归框架)
void MergeSort(int* arr, int* tem, int left, int right)
{
	if (right <= left+1)                  //当子数组只剩一个元素时停止划分
	{
		return;
	}
	int mid = left + (right - left) / 2;
	MergeSort(arr, tem, left, mid);      //划分出的左子数组
	MergeSort(arr, tem, mid, right);     //划分出的右子数组

	//左右子数组都有序后完成左右子数组的归并
}
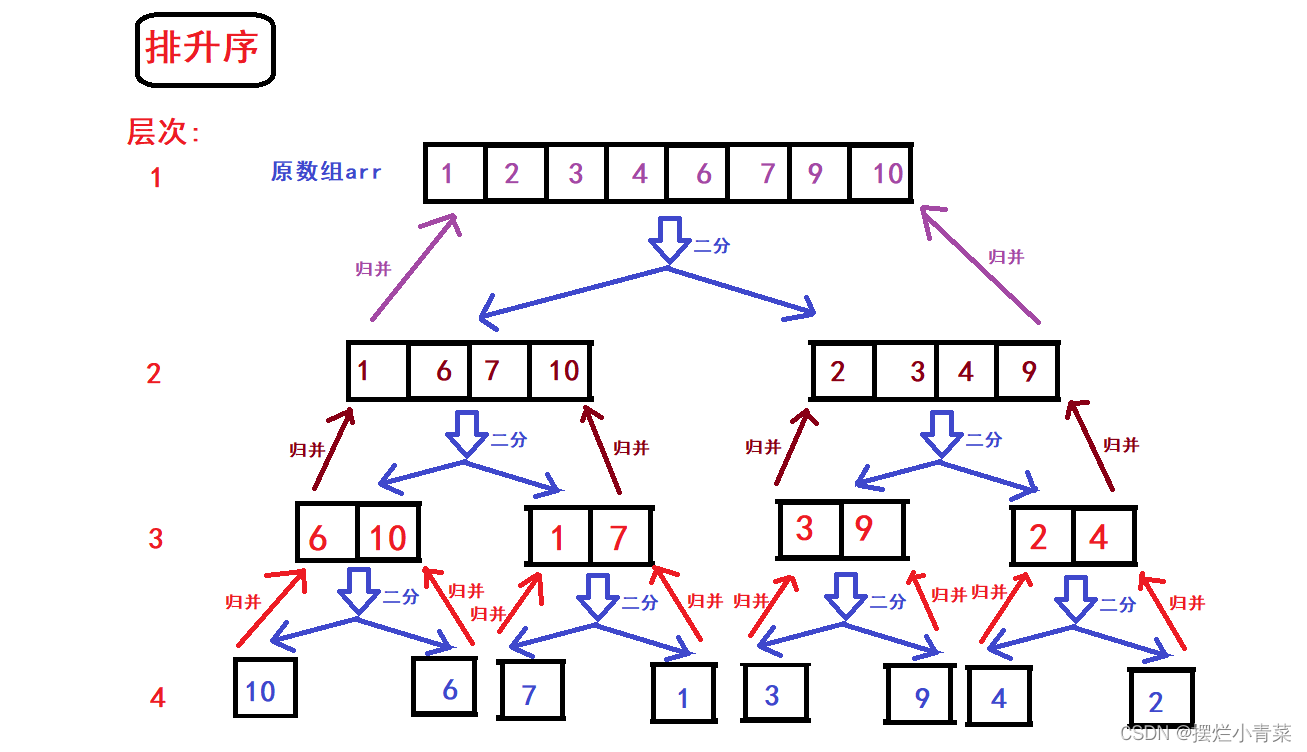
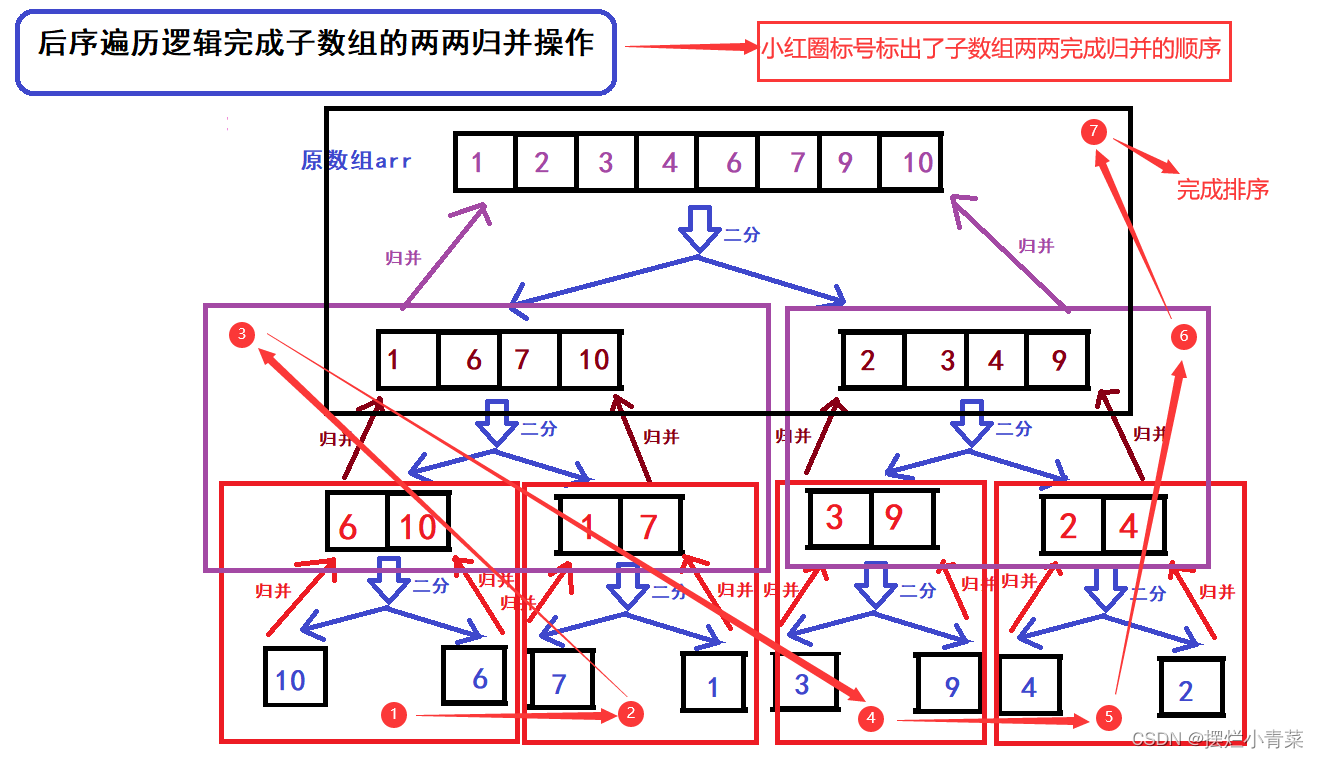
观察递归图解,有序序列两两归并的过程只能发生在上图中的第7,第13,第14,第21,第27,第28,第29步骤中,因此整个排序过程满足分治递归的后序遍历逻辑
递归归并排序的实现:(后序遍历递归)

左右子数组(有序)归并的代码段位于函数中两个递归语句之后
void MergeSort(int* arr, int* tem, int left, int right)
{
	if (right <= left+1)                  //当子数组只剩一个元素时停止划分
	{
		return;
	}
	int mid = left + (right - left) / 2;
	MergeSort(arr, tem, left, mid);      //划分出的左子数组
	MergeSort(arr, tem, mid, right);     //划分出的右子数组
    
    
    //后序遍历,归并过程发生在两个递归语句之后
	//左右子数组都有序后完成左右子数组的归并
	int ptr1 = left;								//ptr1指向左子数组的首元素
	int ptr2 = mid;									//ptr2指向右子数组的首元素
	int ptrtem = left;                              //ptrtem用于在tem数组中尾插数据
	while (ptr1 < mid && ptr2 < right)				//ptr1和ptr2其中一个遍历完子数组就停止循环
	{
		//将较小元素尾插进tem数组中
		if (arr[ptr1] > arr[ptr2])
		{
			tem[ptrtem] = arr[ptr2];
			++ptrtem;
			++ptr2;
		}
		else
		{
			tem[ptrtem] = arr[ptr1];
			++ptrtem;
			++ptr1;
		}
	}
	//将未被遍历完的子数组剩下的元素尾插到tem数组中
	while (ptr1 < mid)
	{
		tem[ptrtem] = arr[ptr1];
		++ptrtem;
		++ptr1;
	}
	while (ptr2 < right)
	{
		tem[ptrtem] = arr[ptr2];
		++ptrtem;
		++ptr2;
	}

	//将归并好的有序序列拷贝到原数组arr(相应下标位置)
	for (int i = left; i < right; ++i)
	{
		arr[i] = tem[i];
	}
}
注意细节:

递归函数抽象分析:

递归函数MergeSort(arr,tem,left,right)可以抽象为：借助tem数组完成arr数组[left,right)区间序列的排序过程
于是可以抽象出递推公式:MergeSort(arr,tem,left,right) = MergeSort(arr,tem,left,left + (right - left) / 2) + MergeSort(arr,tem,left + (right - left) / 2,right) +{子数组[left,left + (right - left) / 2))和子数组[left + (right - left) / 2,right)的有序合并}
递归公式的含义是:完成arr数组[left,right)区间序列排序的过程可以拆分为如下三个步骤:

先完成左子区间[left,left + (right - left) / 2)的排序
再完成右子区间[left + (right - left) / 2,right)的排序
最后将左右子区间进行归并完成[left,right)区间序列的排序
将MergeSort函数进行一下简单的封装供外界调用:
void _MergeSort(int* arr, int size)
{
	assert(arr);
	int* tem = (int*)malloc(sizeof(int) * size);
	assert(tem);
	MergeSort(arr, tem, 0, size);
    free(tem);
}
arr是待排序数组,size是数组的元素个数,MergeSort是归并排序递归函数

四.非递归归并排序的实现

1.非递归归并排序算法思想:

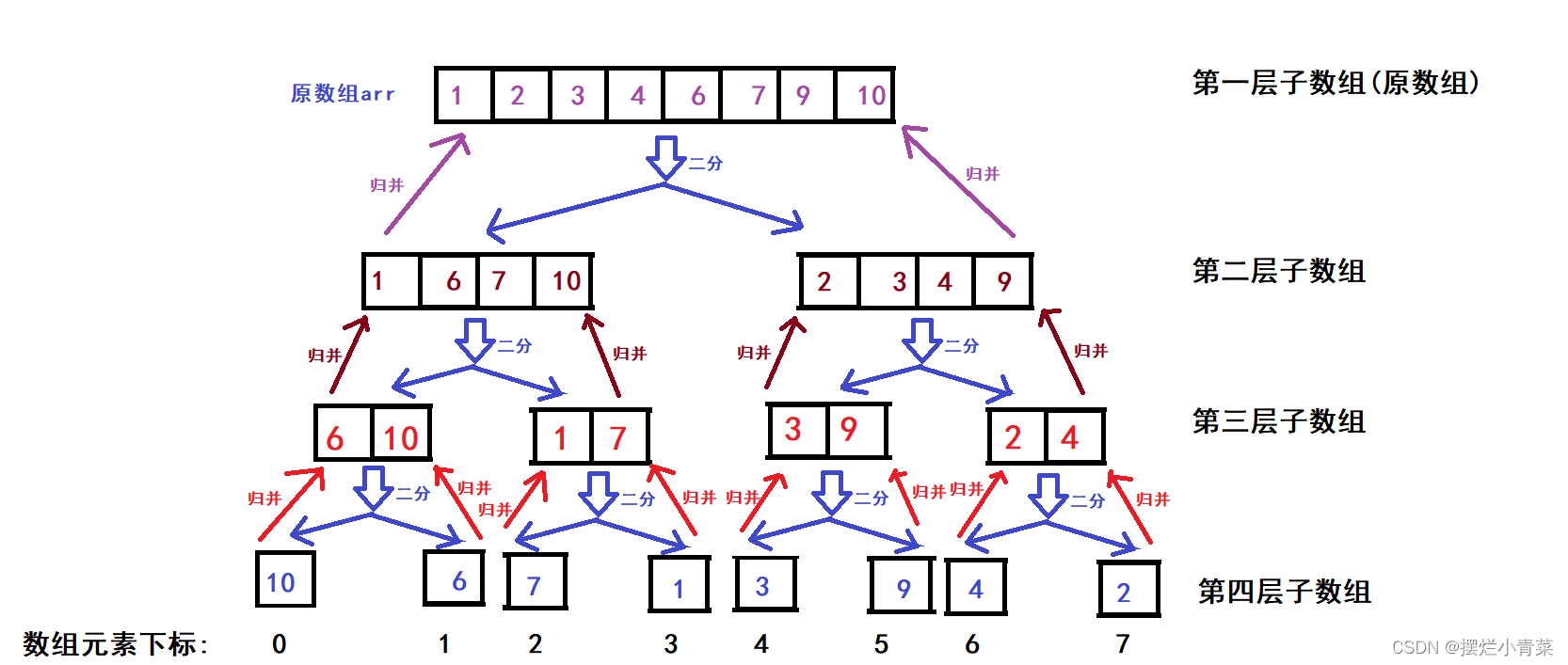
归并排序过程中数组逐步被二分的图示:
归并排序的递归实现通过后序遍历逻辑来完成各个子数组的两两归并的操作:
然而我们也可以利用类似于层序遍历的逻辑来实现子数组两两归并的过程:

从最高层子数组开始进行兄弟子数组的两两归并,完成了一层子数组的归并再继续完成前一层子数组的归并直到最后完成原数组的排序,我们可以通过循环来实现这个过程

2.算法实现

非递归归并排序函数首部:
void MergeSortNonR(int* arr, int size)
arr代表待排序的数组,size为待排序数组的元素个数
先假设所处理的数组的元素个数:N= $2^{n}$ (即数组刚好能被完全二分n次)
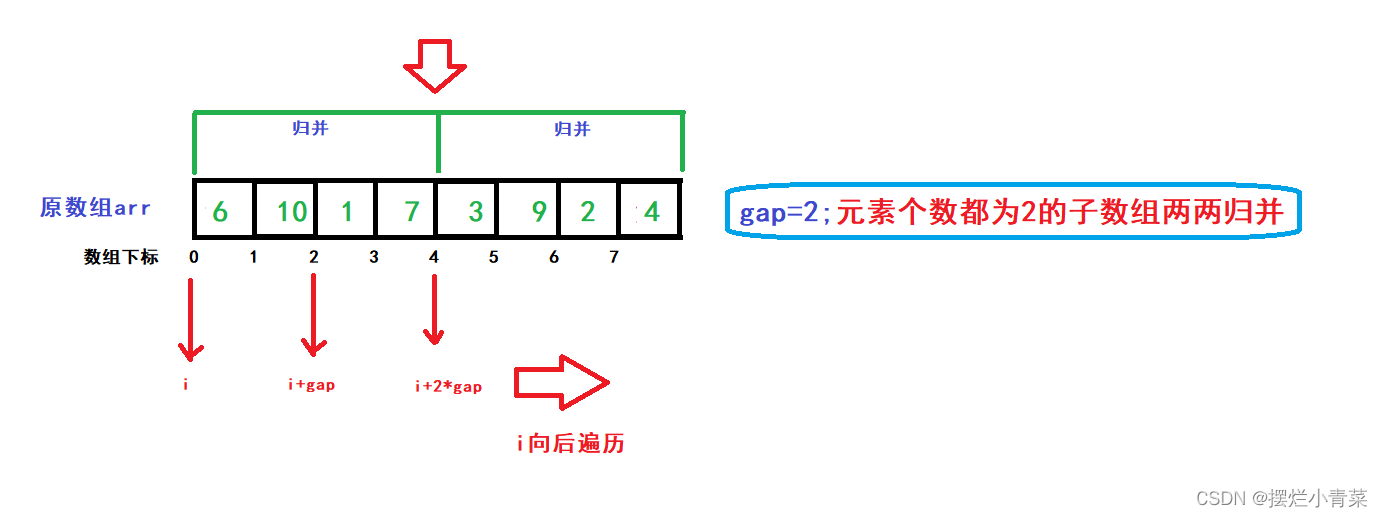
取gap作为二叉树结构某层次各子数组的元素个数:gap初值为1(最深层子数组元素个数为1),随后gap以gap=2*gap的方式递增,用gap来控制排序函数最外层循环:
	for (int gap = 1; gap < size; gap *= 2)   //完成logN个层次的子数组的归并
	{

	}
该循环能进行log(size)次,对于每个gap值完成一个层次的子数组的两两归并:
再使用一个变量i来遍历每一个gap情形下的各个进行归并的序列组(每个序列组由两个子数组构成):
	for (int gap = 1; gap < size; gap *= 2)      //完成logN个层次的子数组的归并
	{
		for (int i = 0; i < size; i += 2 * gap)  //i每次跳过一个归并序列组(每个序列组有两个子数组)
		{
			//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作
		}
	}
图解:
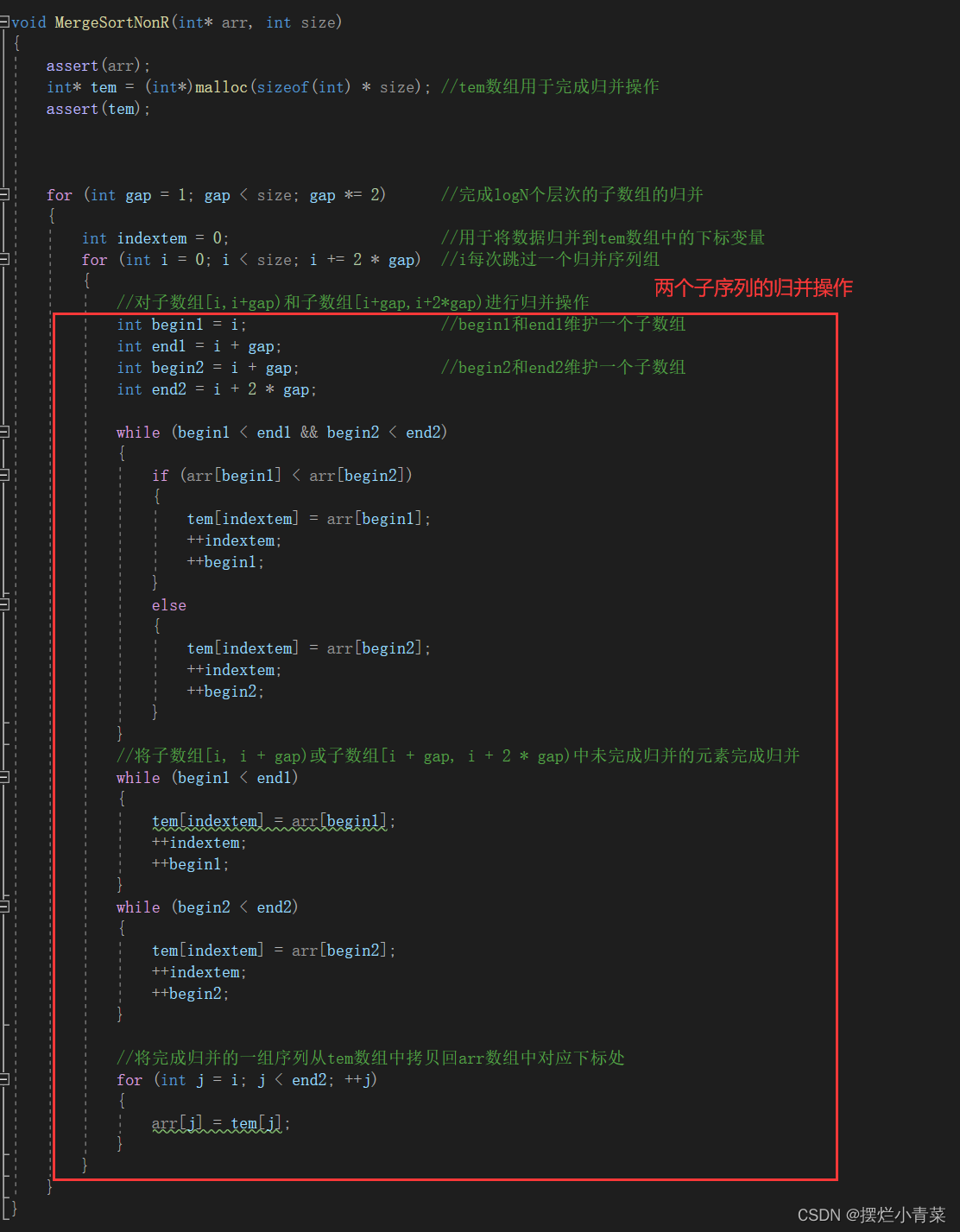
初步非递归归并排序函数:
void MergeSortNonR(int* arr, int size)
{
	assert(arr);
	int* tem = (int*)malloc(sizeof(int) * size); //tem数组用于完成归并操作
	assert(tem);

	

	for (int gap = 1; gap < size; gap *= 2)      //完成logN个层次的子数组的归并
	{
		int indextem = 0;						 //用于将数据归并到tem数组中的下标变量
		for (int i = 0; i < size; i += 2 * gap)  //i每次跳过一个归并序列组(每个序列组有两个子数组)
		{
			//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作
			int begin1 = i;                      //begin1和end1维护一个子数组
			int end1 = i + gap; 
			int begin2 = i + gap;				 //begin2和end2维护一个子数组
			int end2 = i + 2 * gap;

			while (begin1 < end1 && begin2 < end2)
			{
				if (arr[begin1] < arr[begin2])
				{
					tem[indextem] = arr[begin1];
					++indextem;
					++begin1;
				}
				else
				{
					tem[indextem] = arr[begin2];
					++indextem;
					++begin2;
				}
			}
			//将子数组[i, i + gap)或子数组[i + gap, i + 2 * gap)中未完成归并的元素完成归并
			while (begin1 < end1)
			{
				tem[indextem] = arr[begin1];
				++indextem;
				++begin1;
			}
			while (begin2 < end2)
			{
				tem[indextem] = arr[begin2];
				++indextem;
				++begin2;
			}

			//将完成归并的一组序列从tem数组中拷贝回arr数组中对应下标处
			for (int j = i; j < end2; ++j)
			{
				arr[j] = tem[j];
			}
		}
	}

    free(tem);
}
两个子数组的归并操作见前面的章节;

初步非递归归并排序函数只能处理元素个数为 $2^{n}$ (即数组刚好能被完全二分n次)的数组

想要使排序函数能够处理任意元素个数的数组,我们就必须进行算法边界条件分析和边界修正
一般情况下(所排序数组元素个数不为 $2^{n}$ )边界条件分析:

设待排序数组的元素个数为size
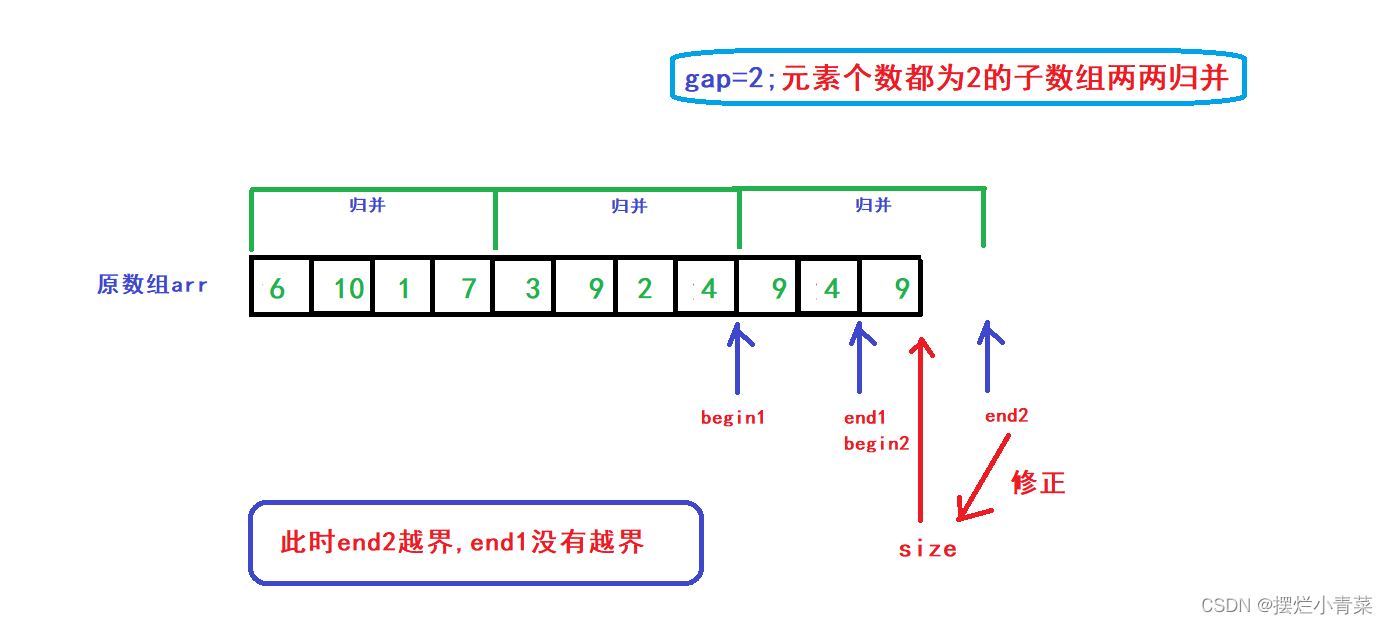
函数中只有下标end1,begin2,end2存在越界的可能(函数中begin1和end1,begin2和end2分别用于维护两个在数组arr中待归并的相邻子数组)

当所处理的数组元素个数不为 $2^{n}$ 时,可能会出现下图中两种下标越界情况

end1(end1==begin2)越界(end1>size)(此时end2一定也越界)此时可以直接break终止i控制的循环(end1>size说明arr数组按照gap划分后尾部待归并区间数量只有一个,无须进行归并操作)

end2越界(end2>size)(end1没越界即(end1<size))

此时要将end2修正为size,后续便可以完成arr数组(按照gap划分后)尾部剩余的两个子数组的归并操作:

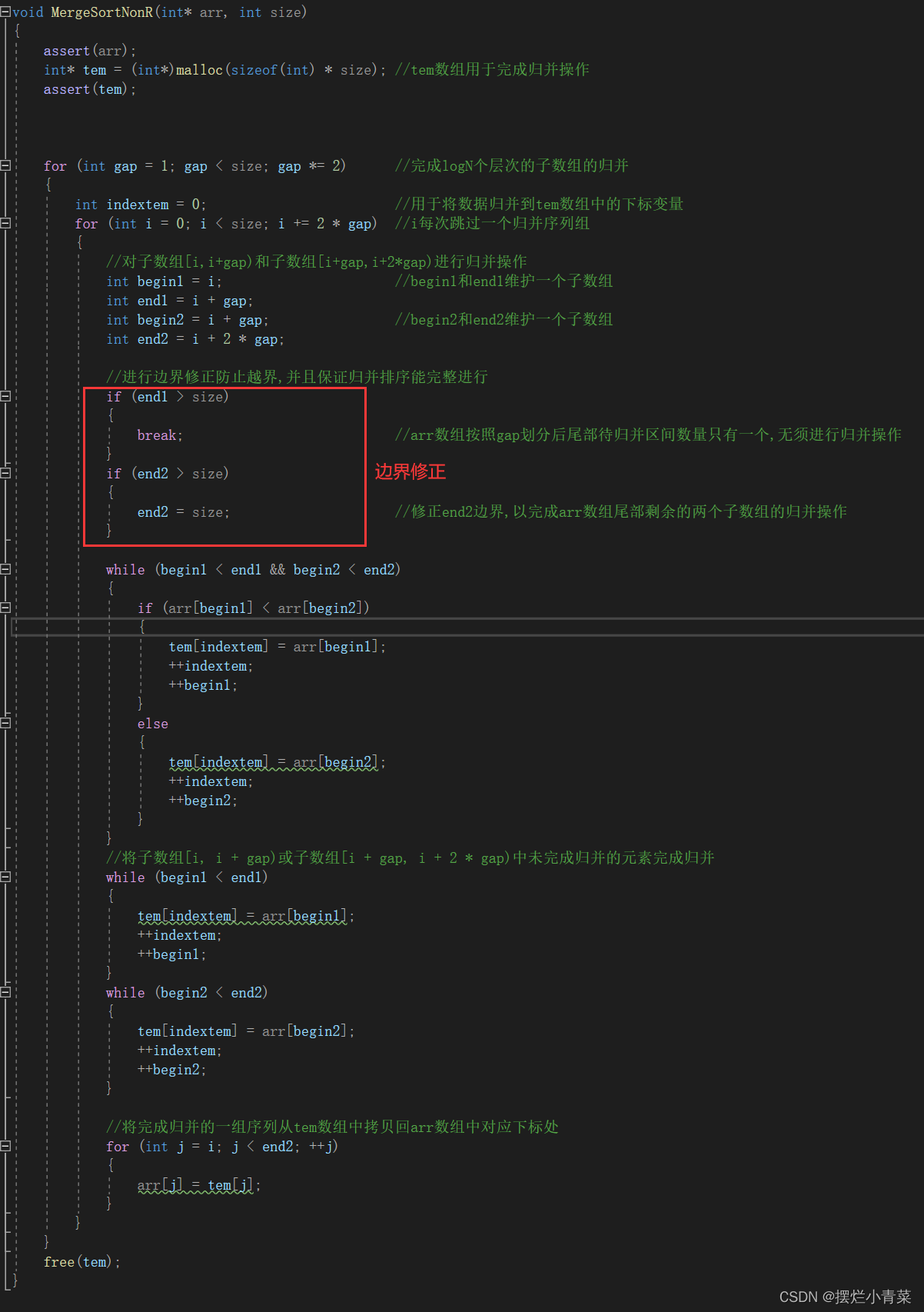
经过边界修正后的非递归归并排序函数
void MergeSortNonR(int* arr, int size)
{
	assert(arr);
	int* tem = (int*)malloc(sizeof(int) * size); //tem数组用于完成归并操作
	assert(tem);

	

	for (int gap = 1; gap < size; gap *= 2)      //完成logN个层次的子数组的归并
	{
		int indextem = 0;						 //用于将数据归并到tem数组中的下标变量
		for (int i = 0; i < size; i += 2 * gap)  //i每次跳过一个归并序列组
		{
			//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作
			int begin1 = i;                      //begin1和end1维护一个子数组
			int end1 = i + gap; 
			int begin2 = i + gap;				 //begin2和end2维护一个子数组
			int end2 = i + 2 * gap;

			//进行边界修正防止越界,并且保证归并排序能完整进行
			if (end1 > size)
			{
				break;                           //arr数组按照gap划分后尾部待归并区间数量只有一个,无须进行归并操作
			}
			if (end2 > size)
			{
				end2 = size;                     //修正end2边界,以完成arr数组尾部剩余的两个子数组的归并操作
			}
			
			while (begin1 < end1 && begin2 < end2)
			{
				if (arr[begin1] < arr[begin2])
				{
					tem[indextem] = arr[begin1];
					++indextem;
					++begin1;
				}
				else
				{
					tem[indextem] = arr[begin2];
					++indextem;
					++begin2;
				}
			}
			//将子数组[i, i + gap)或子数组[i + gap, i + 2 * gap)中未完成归并的元素完成归并
			while (begin1 < end1)
			{
				tem[indextem] = arr[begin1];
				++indextem;
				++begin1;
			}
			while (begin2 < end2)
			{
				tem[indextem] = arr[begin2];
				++indextem;
				++begin2;
			}

			//将完成归并的一组序列从tem数组中拷贝回arr数组中对应下标处
			for (int j = i; j < end2; ++j)
			{
				arr[j] = tem[j];
			}
		}
	}
	free(tem);
}
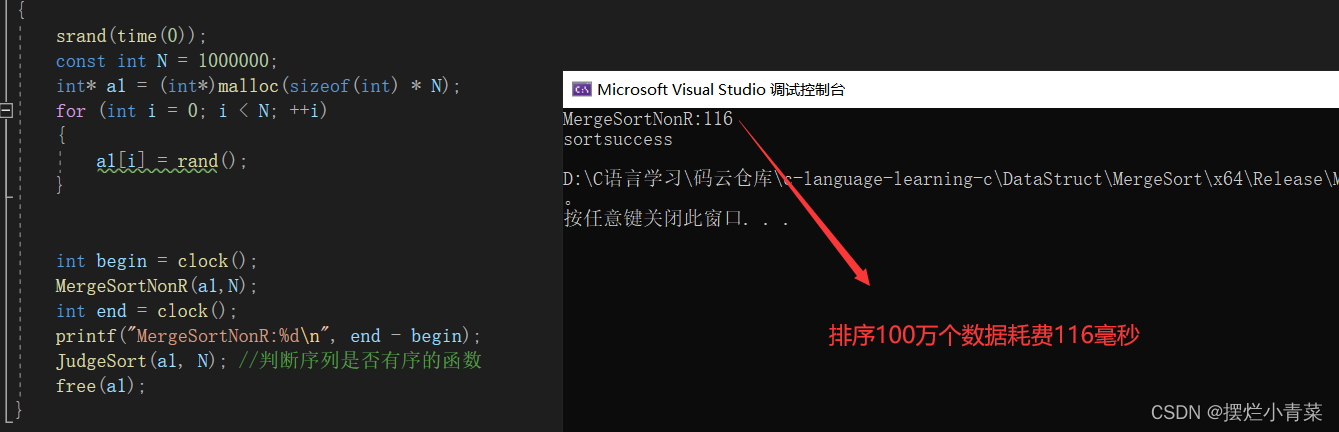
排序实测:
int main()
{
    //排序100万个数据
    srand(time(0));
	const int N = 1000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
	}

	int begin = clock();
	MergeSortNonR(a1,N);
	int end = clock();
	printf("MergeSortNonR:%d\n", end - begin);
	JudgeSort(a1, N); //判断序列是否有序的函数
	free(a1);
}
非递归归并排序和递归归并排序在算法思想上没有任何区别(只是子数组归并的顺序不同而已) 两者的时间复杂度都是O(NlogN),空间复杂度都是O(N)(算法中需要开辟额外的数组tem来完成子序列两两归并操作),但是递归归并排序有额外的系统栈开销.