---

前言

本文是基于《百面深度学习 算法工程师带你去面试》一书，内容也都来自书中，而我会对其中的内容进行些许过滤，将我认为比较重要实用的内容放到博客里，文本虽然来自书中，不过相关的示例图、图片均为本人原创手绘（均带有本人水印）。 如果有人对博客中的图片和动图感兴趣的可以私聊我要无水印的原件。 本系列面向刚入门深度学习的读者，和有一定基础但没有体系了解过深度学习细节的Deep learner。

---

1 卷积基础知识

问题1 简述卷积的基本操作，并分析其与全连接层的区别 （难度：$★$）

分析与解答：

在卷积神经网络出现之前，最常见的神经网络被称为多层感知机（Multi-Layer Perceptron，MLP）。这种神经网络相邻层的节点是全连接的，也就是输出层的每个节点（或者说神经元）会与输入层的所有节点（神经元）连接。如图（a）所示。与全连接网络不同，卷积神经网络主要是由卷积层构成的，它具有局部连接和权值共享等特性，如图（b）所示。

具体来说，卷积层是通过特定数目的卷积核（又称滤波器，filter）对输入的多通道（channel）特征图进行扫描和运算，从而得到多个拥有更高层语义信息的输出特征图（通道数目等于卷积核个数）。Tip：多通道特征图，举个简单例子就是通常的RGB图像可视为三通道的特征图，特征图长和宽与图像像素尺寸一致。

上图形象地描绘了卷积操作的基本过程:下方的绿色方格为输入特征图，蓝色部分是卷积核施加的区域;卷积核不断地扫描整个输入特征图，最终得到输出特征图，也就是上方的橙黄色方格。需要说明的是，输入特征图四周的虚线透明方格，是卷积核在扫描过程中，为了保证输出特征图的尺寸满足特定要求，而对输入特征图进行的边界填充(padding)，一般可以用全零行/列来实现。

以第一个子图(左上角 )为例，可以看到此时卷积核在输入特征图上的滑动位置即为左上角的 3x3 蓝色阴影区域，输入特征图在该区域对应的取值分别为$\left[\begin{array}{ccc}3& 3& 2\\ 0& 0& 1\\ 3& 1& 2\end{array}\right]$，而卷积核的参数取值为$\left[\begin{array}{ccc}0& 1& 2\\ 2& 2& 0\\ 0& 1& 2\end{array}\right]$，所以输出特征图上对应的棕色方格的取值即为上述两个向量的点积，也即:

$3\times 0+3\times 1+2\times 2+0\times 2+0\times 2+1\times 0+3\times 0+1\times 1-2\times 2=12$。

了解了卷积的基本运算过程之后，我们就能更深刻地理解卷积的特性及其与全连接层的区别。

$♣$ 局部连接:

卷积核尺寸远小于输入特征图的尺寸，输出层上的每个节点都只与输入层的部分节点连接。这个特性与生物视觉信号的传导机制类似，存在一个感受野的概念。与此不同，在全连接层中，节点之间的连接是稠密的，输出层每个节点会与输入层所有节点都存在关联。

$♣$ 权值共享:

卷积核的滑动窗机制，使得输出层上不同位置的节点与输入层的连接权值都是一样的(即卷积核参数)。而在全连接层中，不同节点的连接权值都是不同的。

$♣$ 输入/输出数据的结构化:

局部连接和权值共享，使得卷积操作能够在输出数据中大致保持输入数据的结构信息。例如，输入数据是二维图像(不考虑通道)，采用二维卷积，则输出数据中不同节点仍然保持着与原始图像基本一致的空间对应关系;输入数据是三维的视频(即多个连续的视频帧》，采用三维卷积，则输出数据中也能保持着相应的空间、时间对应关系。若是将结构化信息（如二维图像）输入全连接层，其输出数据会被展成扁平的一维数组，从而丧失输入数据和输出数据在结构上的对应关系。

问题2 在卷积神经网络中，如何计算各层的感受野大小 （难度：$★★$）

分析与解答：

在卷积神经网络中，由于卷积的局部连接性，输出特征图上的每个节点的取值，是由卷积核在输入特征图对应位置的局部区域内进行卷积而得到的，因此这个节点的取值会受到该卷积层的输入特征图，也就是上一层的输出特征图上的某个局部区域内的值的影响，而上一层的输出特征图上的每一点的值亦会受到上上一层某个区域的影响。感受野的定义是，对于某层输出特征图上的某个点，在卷积神经网络的原始输入数据上能影响到这个点的取值的区域。
以二维卷积神经网络为例，如果网络的原始输入特征图的尺寸为$L_w\times L_h$，记网络第 $i$ 层节点的感受野大小为$R_e^{(i)}$，其中 e ∈ { w , h } e \in \{w,h\} e∈{w,h}分别代表宽和高两个方向，则可按照式 Eq.1~Eq.4 来计算。

$\cdot$ 若第 $i$ 层为卷积层或池化层( pooling layer)，则有

$R_e^{(i)}=\min (R_e^{(i-1)}+(k_e^{(i)}-1){\prod }_{j=0}^{i-1}{s}_e^{(j)},L_e)(Eq.1)$

其中，$k_e^{(i)}$是第 $i$ 层卷积核/池化核的尺寸，$s$ 是第层的步长。特别地，对于第0层，即原始输入层，有
$\{\begin{array}{l}{R}_e^{(0)}=1\\ s_e^{(0)}=1(Eq.2)\end{array}$
$\cdot$ 若第 $i$ 层为激活层、批归一化层等，则其步长为1，感受野大小为
$R_e^{(i)}=R_e^{(i-1)}(Eq.3)$
$\cdot$ 若第 $i$ 层为全连接层，则其感受野为整个输入数据全域，即
$R_e^{(i)}=L_e(Eq.4)$
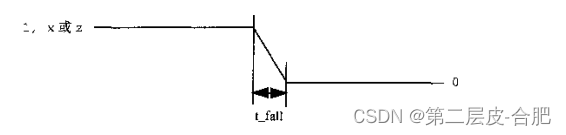
下图为感受野的简单示意图，可以看到，当第 $i-1$ 层和第 $i-2$层的卷积核大小为 $3\times 3$、步长为 1时，使用Eq.1计算可得第 $i$ 层在 $i-1$ 层感受野为$3\times 3$，第 $i$ 层在第 $i-2$ 层上的感受野大小为 $5\times 5$，与图中示例一致。

问题3 卷积层的输出尺寸、参数量和计算量 （难度：$★★$）

假设一个卷积层的输入特征图的尺寸为$l_w^{(i)}\times l_h^{(i)}$，卷积核大小为 $k_w\times k_h$，步长为 $s_w\times s_h$，则输出特征图的尺寸 $l_w^{(o)}\times l_h^{(o)}$ 如何计算? 如果输入特征图的通道数为 $c^{(i)}$，输出特征图的通道数为$c^{(o)}$，在不考虑偏置项(bias)的情况下，卷积层的参数量和计算量是多少?

分析与解答：

$⧫$ 输出尺寸

假设在卷积核的滑动过程中，我们对输入特征图的左右两侧分别进行了 $p_w$ 列填充，上下两侧分别进行了 $p_h$ 行填充，填充后的特征图尺寸为 $(l_w^{(i)}+2p_w)\times (l_h^{(i)}+2p_w)$，则输出特征图的尺寸为
l e ( o ) = l e ( i ) + 2 p e − k e s e + 1 , e ∈ { w , h } l_e^{(o)} = \cfrac{l_e^{(i)} + 2 p_e-k_e}{s_e} + 1, e \in \{ w,h\} le(o)​=se​le(i)​+2pe​−ke​​+1,e∈{w,h}

上述公式在步长 $s_e>1$ 时，可能会出现非整数情况，此时，很多深度学习框架会采取向下 取整的方式，放弃输入特征图的一部分边界数据，使得最终的输出特征图的尺寸为
l e ( o ) = ⌊ l e ( i ) + 2 p e − k e s e ⌋ + 1 , e ∈ { w , h } l_e^{(o)} = \bigg\lfloor\cfrac{l_e^{(i)} + 2 p_e-k_e}{s_e}\bigg\rfloor + 1, e \in \{ w,h\} le(o)​=⌊se​le(i)​+2pe​−ke​​⌋+1,e∈{w,h}

例如，Caffe和PyTorch 会放弃输入特征图的左侧和上侧的一部分数据使得卷积核滑动窗恰好能到达最右下角的点。
有些深度学习框架(如 TensorFlow、Keras)在做卷积运算时无法显式指定输入特征图的边界填充尺寸(当然可以在做卷积之前手动填充)，只能选择以下几种预先定义好的填充模式。
$\cdot$ 若选择 padding-same 模式，则会在输入特征图的左右两侧一共填充 $p_w^{+}=k_w-1$ 列，上下两侧一共填充$p_h^{+}=k_h-1$行，最终的输出特征图的尺寸为
l e ( o ) = ⌊ l e ( i ) − 1 s e ⌋ + 1 , e ∈ { w , h } l_e^{(o)} = \bigg\lfloor\cfrac{l_e^{(i)}-1}{s_e}\bigg\rfloor + 1, e \in \{ w,h\} le(o)​=⌊se​le(i)​−1​⌋+1,e∈{w,h}

例如在 TensorFlow 中，如果$p_e^{+}$为偶数，则在输入特征图的左右两侧或上下两侧填充相等数目的列/行；如果为奇数，会让右侧/下侧比左侧/上侧多填充一列/行。
$\cdot$ 若选择padding=valid模式，则不会对输入特征图进行边界填充而是直接放弃右侧和下侧卷积核无法滑动到的区域，此时输出特征图的尺寸为
l e ( o ) = ⌊ l e ( i ) − k e s e ⌋ + 1 , e ∈ { w , h } l_e^{(o)} = \bigg\lfloor\cfrac{l_e^{(i)}-k_e}{s_e}\bigg\rfloor + 1, e \in \{ w,h\} le(o)​=⌊se​le(i)​−ke​​⌋+1,e∈{w,h}

$⧫$ 参数量

卷积层的参数量，主要取决于每个卷积核的参数量以及卷积核的个数。在这里，每个卷积核含有 $c^{(i)}\times k_w\times k_h$ 个参数，而卷积核的个数即输出征图的通道个数 $c^{(o)}$，因此参数总量为

$c^{(i)}\times c^{(o)}\times k_w\times k_h$

$⧫$ 计算量

卷积层的计算量，由卷积核在每个滑动窗内的计算量以及整体的清动次数决定。在每个滑动窗内，卷积操作的计算量大约为 $c^{(i)}\times k_w\times k_h$，而卷积核的滑动次数即输出特征图的数据个数，也就是$c^{(o)}\times l_w^{(o)}\times l_h^{(o)}$，因此整体的计算量为

$c^{(i)}\times c^{(o)}\times l_w^{(o)}\times l_h^{(o)}\times k_w\times k_h$

一般情况下，有 k e ≪ l e ( i ) , k e ≪ l e ( i ) , e ∈ { w , h } k_e \ll l_e^{(i)}, k_e \ll l_e^{(i)}, e \in \{ w,h\} ke​≪le(i)​,ke​≪le(i)​,e∈{w,h}，因此上式可以近似简写为

$\frac{c^{(i)}\times c^{(o)}\times l_w^{(i)}\times l_h^{(i)}\times k_w\times k_h}{(s_w\times s_h)}$

未完待续……

2 卷积的变种

问题1 简述转置卷积的主要思想以及应用场景

问题2 简述空洞卷积的设计思路

3 卷积神经网络的基础模块

问题1 批归一化是为了解决什么问题？它的参数有何意义？它在网络中一般放在什么位置？

问题2 卷积神经网络中的瓶颈结果和沙漏结构提出的初衷是什么？可以应用于哪些问题？