【人工智能里的数学】多元函数的微分学

系列文章目录

【人工智能学习笔记】人工智能里的数学——概述
【人工智能里的数学】一元函数微分学
【人工智能里的数学】线性代数基础
【人工智能里的数学】多元函数微分学

文章目录

偏导数

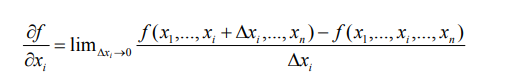
偏导数，可以看作是导数的推广，对于多元函数来说，我们把其它的自变量固定不动，看成是常量，我们对其中的某一个变量求导数的话，那就是偏导数了，偏偏对一个变量求导数！

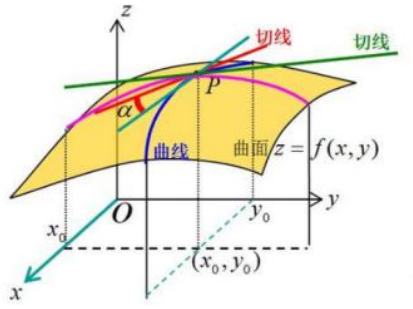
几何意义上面来说就是在某个方向上对原函数来切一下，再去求导，就是偏导数

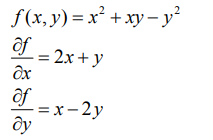
有些时候我们也可以更简洁的写

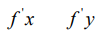
高阶偏导数

有高阶导数的话，同样我们有高阶偏导数，它的情况比高阶导数要复杂一些，因为它的求导变量有多个，比如说

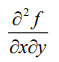
它对 x,y 求高阶偏导数的话，就是先对 x 求偏导，再对 y 求偏导，其实跟一元函数的高阶导数是一样的，依次对每个变量反复求导呗，我们还是以上面的公式为例

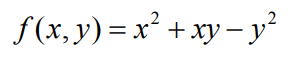
对 x 求偏导，然后再对 x 求偏导就等于 2 了

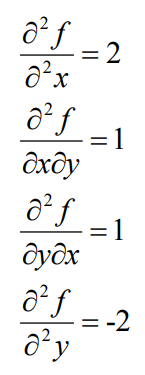
有个重要的结论，就是高阶导数和求导次序无关

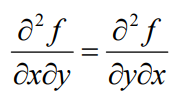
梯度

机器学习中的梯度下降法，和牛顿法很多地方都会用到这个概念的

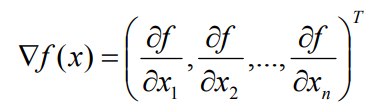
梯度可以看成是一元函数它的导数，对于多元函数的推广

对于多元函数如果它的自变量有 N 个

它的梯度是个向量，是由对 X1 X2 等的偏导数构成的这样一个向量，称之为梯度

梯度我们用倒三角这个符号来表示作用于 f(x)得到这样一个向量，式子里面的 T 表示往往我们把它转置一下，看成是列向量

雅可比矩阵

这个可能很多同学学高等代数的时候可能没有学过，但是这个也比较好理解，就是由一阶偏导数构成的矩阵，发明它的目的主要是为了简化求导公式，对多元的复合函数求导，如果我们用雅可比矩阵来计算的话，它会写起来非常简洁，这在我们的人工神经网络反向推导的过程中往往会看到的

假设有这样一个函数可以把 n 维 x 向量映射为 k 维的向量 y

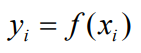
其中每个 xi 和每个 yi 都相关的，也就是每个 yi 是单独从 xi 映射过来的函数

它的雅可比矩阵就是每个 yi 分别对每个 xi 求偏导，然后构成的矩阵叫做雅可比矩阵

第一行就是 y1 对 X1 X2 到 Xn 求偏导，第二行就是 y2 对 X1 X2 到 Xn 求偏导，第 k 行就是 yk 对 X1 X2 到 Xn 求偏导，

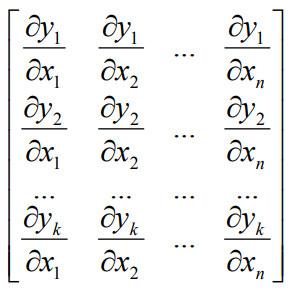
如果 xi 是 n 维向量，y 是 k 个值的结果，那么雅可比矩阵就是 k*n 的矩阵

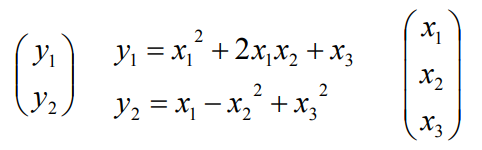
如果 x1,x2,x3 会映射成为 y1,y2，y1 是 x1,x2,x3 的函数，y2 也是 x1,x2,x3 的函数，那么它的雅可比矩阵是怎么构成的呢？

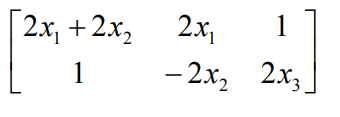
Hessian 矩阵

它是对于一个多元函数来说的，它就相当于一元函数的二阶导数

怎么定义的呢？有一个 n 元函数，比方说 X1，X2 一直到 Xn

它的 hessian 矩阵是一个 n*n 的矩阵，矩阵里面的元素是什么呢？

它的所有的元素是二阶偏导数构成的，第一个元素是对 X1 求二阶偏导数，第二个元素是对 X1X2 求偏导数，因为咱们前面讲过，多元函数高阶偏导数和顺序无关，所以 hessian 矩阵是对称矩阵

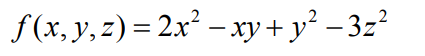
下面这个例子先看一下它的一阶偏导数

然后把 hessian 矩阵求出来

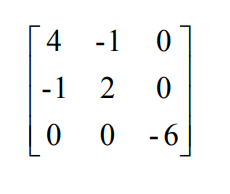
Hessian 矩阵和函数的凹凸性是有密切关系的，如果 hessian 矩阵正定，可以说函数 f(x)是凸函数，如果是负定，它就是凹函数，矩阵正定怎么定义的呢？

极值判别法则

对于一元函数，我们前面讲过，f(x)的一阶导数等于 0 处有极值，当 f(x)的二阶导数大于 0时是极小值，当 f(x)的二阶导数小于 0 时是极大值，可以参考 X 的平方这个函数

多元函数的极值判别法则

首先 f(x)的一阶导数等于 0，这点是驻点的话，那它就可能是极值点，它是极大值还是极小值或者不是极值怎么判定的？

看 hessian 矩阵，在 f(x)的一阶导数等于 0 处，就是驻点处，如果 hessian 矩阵是正定的话，函数在该点有极小值

如果 hessian 矩阵是负定的话，函数在该点有极大值如果 hessian 矩阵不定，还需要看更高阶的导数

对于任意向量 X≠0，都有 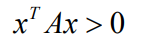，那就是正定矩阵，如果是≥的话，那就是半正定矩阵

怎么判断矩阵是正定的呢？就是拿这个式子去证明，

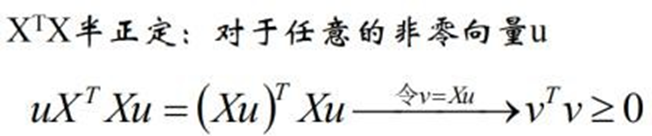
但是这样不太容易，有时候我们会根据几个原则去判断：

矩阵的特征值全部大于 0（矩阵的特征值和特征向量我们会讲到） 矩阵的所有顺序主子式都大于 0（顺序主子式这个我们用的比较少）矩阵合同于单位阵
.(img-2K8dUJuE-1686658156231)]

但是这样不太容易，有时候我们会根据几个原则去判断：

矩阵的特征值全部大于 0（矩阵的特征值和特征向量我们会讲到） 矩阵的所有顺序主子式都大于 0（顺序主子式这个我们用的比较少）矩阵合同于单位阵