前言

在CTR预估中，FM系列模型使用浅层网络（线性模型），让模型自己学习特征组合交互，为显式建模的方式；而DNN系列模型使用深层网络，隐式挖掘模型的高阶特征交互。

本文继续介绍结合这两者优点的另外一个系列：Wide&Deep，即同时加入低阶特征组合交互的线性模型-Wide、高阶特征交叉的深度模型（Deep），Wide部分模型提供模型的记忆能力，而Deep部分提供模型的泛化能力。这是Wide&Deep系列模型很重要的一个点。

Wide & Deep

论文：Wide & Deep Learning for Recommender Systems

地址：https://arxiv.org/pdf/1606.07792.pdf

论文指出推荐系统的其中一个挑战在于同时兼顾memorization（记忆）和generalization（泛化）：

1. 记忆能力可以宽松地定义为从历史数据中学习items和特征的共现和相关性，对应逻辑回归这样的线性模型的学习模式，但它们不够泛化，无法处理训练样本中未出现过的query-item特征对；
2. 泛化则是另外一方面的能力：相关性的传递和对于新的特征组合的探索，对应深度神经网络，通过将为特征学习一个低维的embedding向量来获得这样的泛化能力，但对于那些频次很低的query和item，学习一个有效的向量表征是困难的，比如有些用户的偏好是很狭隘少见的，那么它们应该跟大部分query-item pairs是没有交互的，但稠密向量会导致所有query-item pairs是nonzero的，直白说就是强行交互了，过度泛化了，因此出现无关的推荐；
3. 另一方面，带有cross-product特征变换的线性模型，可以用很少的参数，记住（memorize）那些例外的规则（exception rules）。

论文提出的Wide & Deep学习框架就是为了兼具记忆和泛化，联合训练一个线性模型组件和一个深度神经网络模型组件，如下图：

Wide Component

Wide组件是一个普通的线性模型，如上图[Wide&Deep框架]-左：$y=w^{T}x+b$

其中，y是预估值，x是一个向量，包含了d个特征值 $x=[x_1,x_2,...,x_d]$，w是模型的参数 $w=[w_1,w_2,...,w_d]$，而b则是bias。

值得注意的是，x包括了原设的特征输入，还有变换过的特征，论文列出一个最重要的特征变化：cross-product

$c_{ki}$是一个布尔变量，当第i个特征是第k个变换的一部分，取值为1，否则为0。比如有一个cross-product变换为“AND(gender=female, language=en)”，那么当且仅当所有组成特征都为1时，${\varphi }_k$才等于1，其他情况都为0。

再对应解释下$c_{ki}$，如另外的特征(city)由于不是这个变换的部分，那么$c_{ki}$为0，任何取值下$x_i^{c_{ki}}$都为1，不影响最终的${\varphi }_k$。

Deep component

Deep组件是一个前馈神经网络，如上图[Wide&Deep框架]-右。老生常谈，对于类别特征，原设输入是字符串(如‘language=en’，language有许多取值)，每一个这样稀疏和高维的特征都会转换为一个低维和稠密的实值向量，即embedding vector。这些embedding vectors会被输入到神经网络的隐藏层：

其中，l是隐藏层的数量，f是激活函数（一般为ReLUs）。

联合训练

在这里，论文还说明了集成学习和联合训练的区别：

• 集成学习中，每个独立的模型在训练阶段是分开，无法获取其他模型的知识，仅仅在推理阶段组合它们的预测。而正是集成学习的训练不交叉的缘故，每个独立的模型规模通过会比较大，以为了能够取得更好的效果；
• 而联合训练在训练时，包括wide和deep组件，所有参数是同步更新的。wide组件是为了deep组件的弱势，因此wide组件仅仅是一些少量的cross-product特征变换。

在联合训练中，wide组件使用的优化器是带有L1正则的Follow-the-regularized-leader (FTRL)，而deep组件使用的AdaGrad，最终组合的模型正如上图[Wide&Deep框架]-中，形式如下：

其中，$\sigma (\cdot )$是一个sigmoid函数，$a^{(l_f)}$是最后一层网络经过激活函数的输出。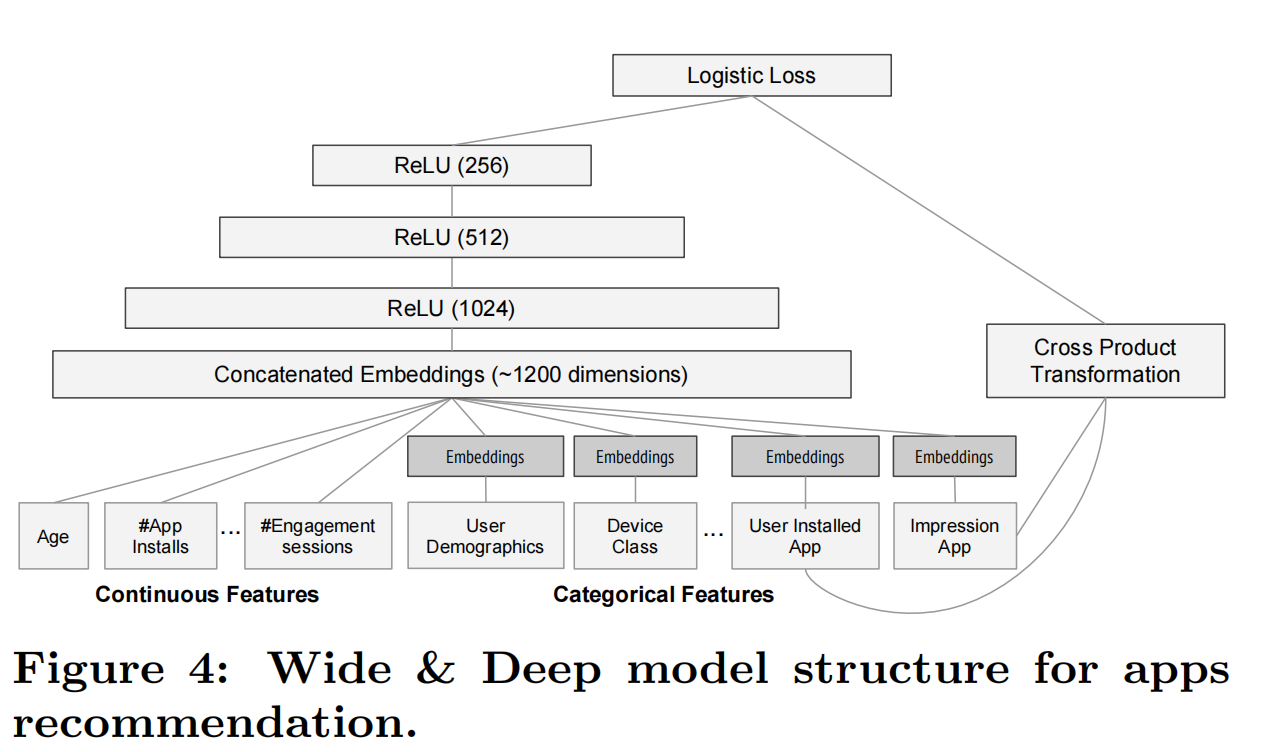

DeepFM

论文：DeepFM: A Factorization-Machine based Neural Network for CTR Prediction

地址：https://www.ijcai.org/proceedings/2017/0239.pdf

DeepFM模型仍然可以认为是套用Wide&Deep的基础框架，但是DeepFM模型在以下几点上做了一些改进：

• wide部分使用了FM模型，来替代线性模型；
• wide和deep部分共享了同样的输入；
• wide和deep部分共享了feature embedding；
• FM可以代替原来wide组件中的交叉特征工程，而feature embedding共享可以让模型同时学习低阶特征和高阶特征的交互能力。

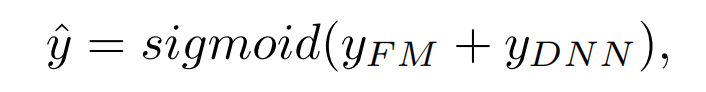
对于FM模型系列，可以跳转到这篇文章FM/FFM/FwFM/FEFM

论文做了详细的超参数消融实验，具体结果如下图所示：

其中network shape表示：constant (200-200-200)、increasing (100-200-300)、decreasing (300-200-100)、diamond (150-300-150).

Deep&Cross（DCN）

论文：Deep & Cross Network for Ad Click Predictions

地址：https://arxiv.org/pdf/1708.05123.pdf

Deep & Cross Network (DCN)与DeepFM模型一样，基于Wide & Deep的框架，对wide部分进行改进：使用cross network，能够学习超过二阶的特征交互，同样可以摆脱人工特征工程。DCN模型结构如下图：

1. 离散特征转化为embedding向量，然后与连续性特征进行拼接；
2. 拼接后的特征，分别输入到多层MLP和Cross Network；
3. 与DeeFM不同的是，MLP和Cross network不是输出标量，而是向量；
4. 最后，MLP和Cross Network的输出向量进行拼接，再经过一层MLP(与权重相乘加上偏置)，使用sigmoid函数得到最终的输出预测概率。

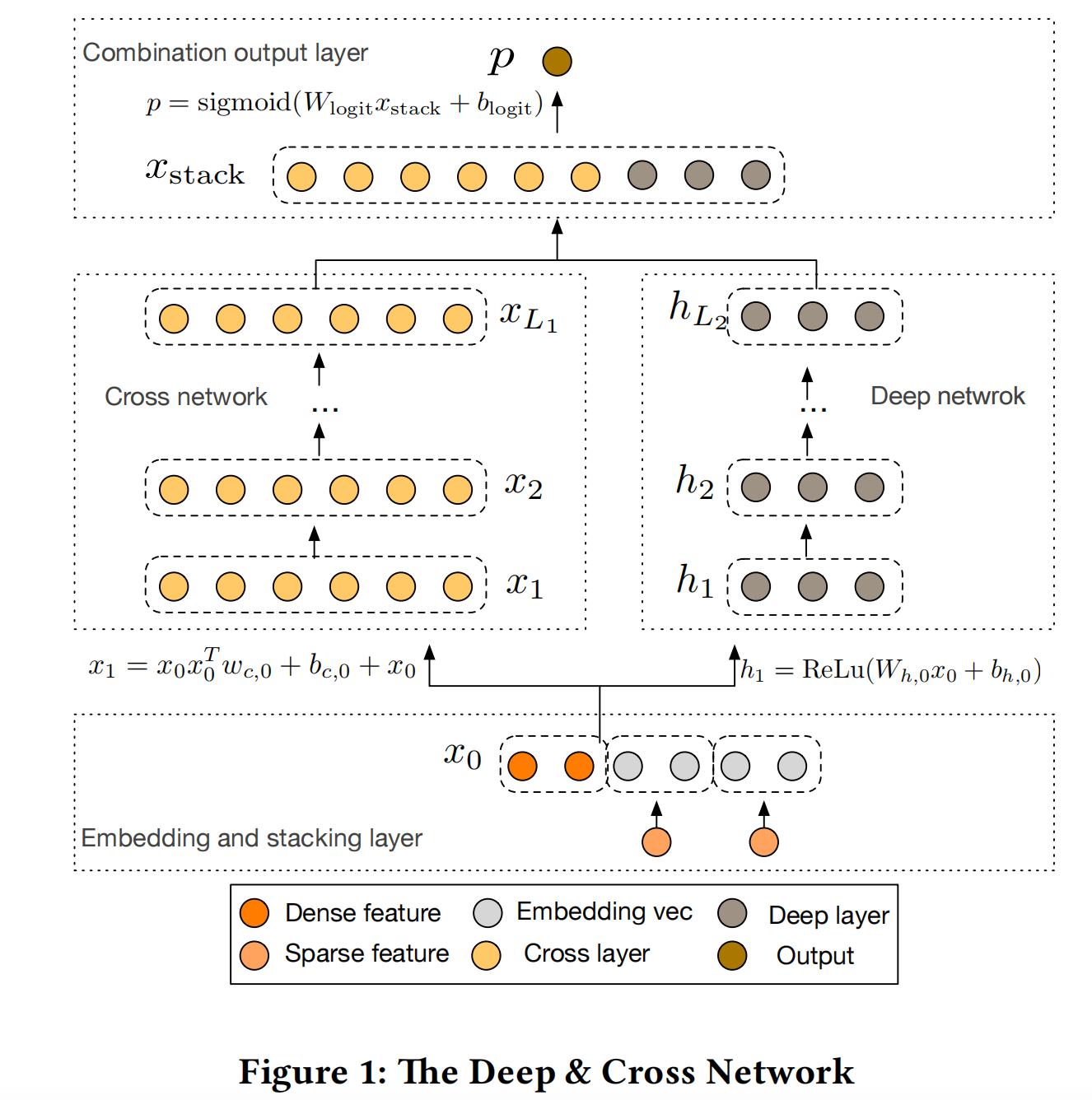
DCN中除了Cross network，其他部分与其他模型的基本一致，因此不再赘述，着重讲解cross network部分。

Cross Network

Cross Network是这篇论文的核心创新点-显示的特征交叉，它的公式形式如下式：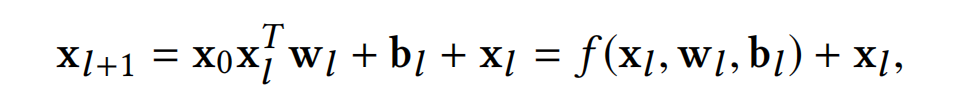

其中，$x_0$即是特征embedding拼接输入，$x_{l+1},x_l\in {\mathbb{R}}^d$是d维的向量，分别代表第l和l+1层cross layer的输出，并且第l层在特征交叉(feature cross)之后，会加回原来的输入$x_l$，即让feature cross去拟合第l+1层与第l层的残差：$x_{l+1}-x_l$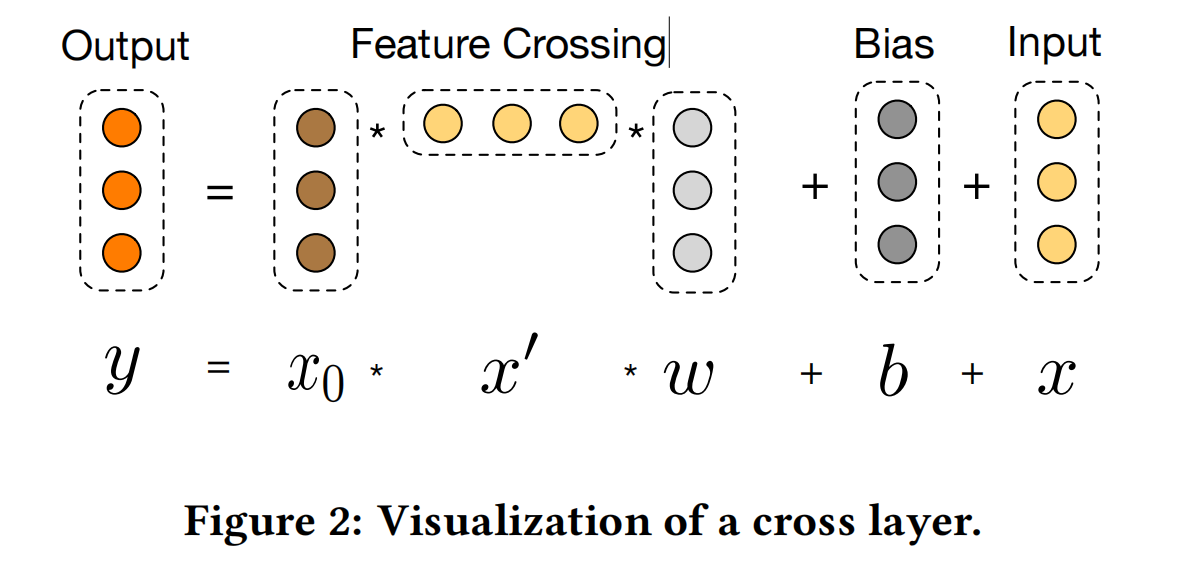

可以看出l层的cross network能够达到l+1阶的特征交叉，并且参数量仅为d的的线性关系：$d\times l\times 2$

论文从三种角度来帮助分析理解cross network的有效性：polynomial approximation、generalization to FMs、efficient projection。在分别介绍这三种分析方法之前，先说明一些参数符号：

• $w_j^{(i)}是w_j$的第i个元素
• 交叉项索引：$\alpha =[{\alpha }_1,{\alpha }_2,...,{\alpha }_d]\in {\mathbb{N}}^d，|\alpha |={\sum }_{i=1}^d{\alpha }_i$
• $x=[x_1,x_2,...,x_d]$
• $|\alpha |$决定了交叉项$x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdot \cdot \cdot x_d^{{\alpha }_d}$的阶数，比如$\alpha =[1,0,1,0]$即代表了2阶交叉，且交叉项为$x_1{x}_3$

Polynomial Approximation

对于n阶的多元(d元)多项式为，它的系数数量达到了$O(d^n)$，如下式：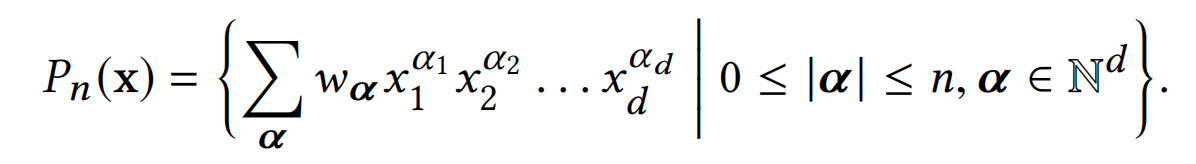

但是，论文提出的cross network能够以O(d)的参数量，包含了上式多元多项式的所有交叉项，并且每个交叉项的系数都是不同的。

考虑一个l层的cross network，并且第i+1层的输出为：$x_{i+1}=x_0{x}_i^T{w}_i+x_i$。

让输入为$x_0=[x_1,x_2,...,x_d]$，输出为$g_l(x_0)=x_l^T{w}_l$，参数为$w_i,b_i\in {\mathbb{R}}^d$，然后多元多项式$g_l(x_0)$可以变为下式：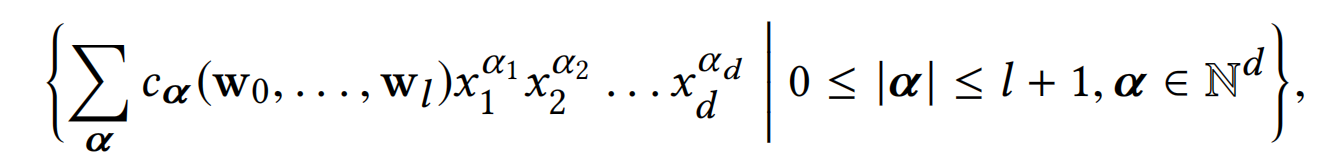

• 其中，$c_{\alpha }=M_{\alpha }{\sum }_{i\in B_{\alpha }}{\sum }_{j\in P_{\alpha }}\Pi w_{i_k}^{(j_k)}$，
• $M_{\alpha }$是一个与w无关的独立常量，
• $i=[i_1,i_2,...,i_{|\alpha |}]和j=[j_1,j_2,...,j_{|\alpha |}]$都是交叉项索引， B α = { y ∈ { 0 , 1 , . . . , l } ∣ α ∣ ∣ y i < y j ∧ y ∣ α ∣ = l } B_\alpha=\{y\in \{0,1,...,l\}^{|\alpha|}|y_i<y_j \wedge y_{|\alpha|}=l\} Bα​={y∈{0,1,...,l}∣α∣∣yi​<yj​∧y∣α∣​=l}，
• $P_{\alpha }=\underset{{\alpha }_{1}times}{\underbrace{1,...,1}}...\underset{{\alpha }_{d}times}{\underbrace{d,...,d}}$，是交叉项索引的所有排列组合。
• 举个例子，对于交叉项$x_1{x}_2{x}_3$，有 α = { 1 , 1 , 1 , 0 , . . . , 0 } \alpha=\{1,1,1,0,...,0\} α={1,1,1,0,...,0}，第2层即l=2时，$c_{\alpha }={\sum }_{i,j,k\in P_{\alpha }}{w}_0^{(i)}{w}_1^{(j)}{w}_2^{(k)}$。而第3层即l=3时，$c_{\alpha }={\sum }_{i,j,k\in P_{\alpha }}{w}_0^{(i)}{w}_1^{(j)}{w}_3^{(k)}+w_0^{(i)}{w}_2^{(j)}{w}_3^{(k)}+w_1^{(i)}{w}_2^{(j)}{w}_3^{(k)}$
• 以上公式可以辅助下图展开进行理解：

可以看出，1、cross network的参数量能够比普通的多元多项式少的原因在于：参数w的共享，但每个特征交叉项又使用了不同的参数交叉，以达到不同系数的效果；

2、cross network是以bit-wise的方式来实现高阶特征交叉的。

Generalization of FMs

cross network借鉴了FM模型的参数共享的精髓，并且将其扩展到更深的结构。

• 在FM模型中，特征$x_i$跟着权重向量$v_i$，它与$x_j$的交叉项$x_i{x}_j$的权重由$<v_i,v_j>$计算而来。但DCN中，$x_i$的权重则是标量 { w k ( i ) } k = 1 l \{w_k^{(i)}\}^l_{k=1} {wk(i)​}k=1l​，交叉项$x_i{x}_j$的权重则变成了 { w k ( i ) } k = 0 l \{w_k^{(i)}\}^l_{k=0} {wk(i)​}k=0l​和 { w k ( j ) } k = 0 l \{w_k^{(j)}\}^l_{k=0} {wk(j)​}k=0l​两个集合的相乘
• 参数共享不仅可以使模型更加高效，对于训练样本中无共现的特征交叉，还能起到泛化的作用，更具鲁棒性，这也是FM模型的一个重要创新点
• 但是FM模型只限于二阶交叉，相比之下，DCN可以实现所有交叉项$x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdot \cdot \cdot x_d^{{\alpha }_d}$的$|\alpha |=l+1$阶交叉，由cross network的层数决定，并且参数量只是与输入维度d是线性关系。

Efficient Projection

记$\tilde{x}$为每一层的cross layer的输入，cross layer实现的其实就是隐式的组合$\tilde{x}$和x的所有pairwise interactions $x_i{\tilde{x}}_j$（$d^2$个），然后再隐式的投影(project)到维度d，有效将参数量由维度d的三次方减少到线性关系，从这里也可以看出参数量的减少得益于参数w共享：其中，$w\in {\mathbb{R}}^d$。回归到DCN，x则为$x_0$，那么$x_P=x_0{\tilde{x}}^{T}w$

实验结果

论文使用的数据集是：Criteo Display Ads Data，实验得到最好的结构是6层cross layer和2层1024size的deep layer，其他参数如下：

• batch_size为512
• 使用Adam优化器，并且梯度裁剪norm为100
• 学习率使用的递增方式，从0.0001到0.001，增值为0.0001

从下图也可以看出，加入cross layer之后，效果提升显著

DCN V2

论文：DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems

地址：https://arxiv.org/pdf/2008.13535.pdf

2017年提出DCN之后，该团队在2020年发表DCN-V2版本的论文，与DCN的区别在于Cross Network，在特征对交叉使用的权重使用了矩阵的形式，而DCN是向量形式，如下图所示：

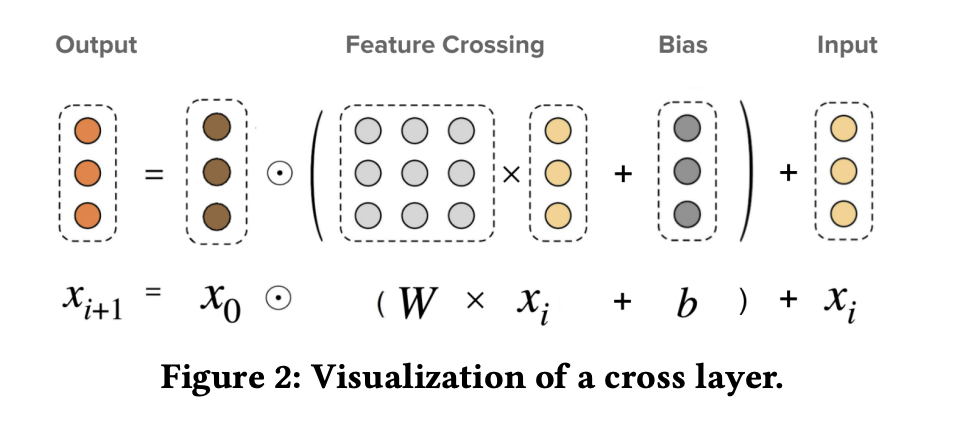
但这样带来的参数量提升是巨大的，由原来的O(d)变为$O(d^2)$。因此引入一种low-rank的方法，即将原来输入的直接投影（project），调整为先投影到低维度空间${\mathbb{R}}^r$，再重新投影回原来的维度${\mathbb{R}}^d$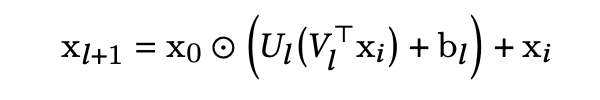

当r<<d时，参数量可以显著减少。$U_l,V_l\in {\mathbb{R}}^{d\times r}$

上述，DCN是以bit-wise的方式来实现高阶特征交叉的，而DCN-V2不仅能视为bit-wise的交叉方式（可认为是cross network中权重w没有共享的的DCN，如下图[efficient projection]），也能够看成是feature-wise。

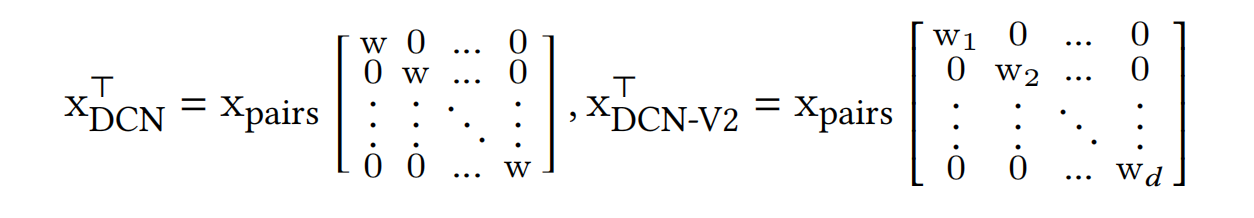
总结

Wide & Deep提出一种通用框架：wide组件的线性模型的显性低阶特征交叉提供记忆能力，deep组件的深度网络模型的隐式高阶特征交叉提供泛化能力；

DeepFM模型则是在此基础，加强wide部分的能力，将线性模型替换为FM模型，并且大大减少特征工程；

Deep & Cross又是进一步提升wide部分的能力，突破FM浅层网络的二阶特征交叉能力限制，使用深层网络来实现高阶的显式特征交叉，并且参数量能够保持在输入维度的线性关系。

代码实现

DCN

DeepFM