力扣 1483. 树节点的第 K 个祖先
题目地址:https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/
- 暴力查找(超时)
- 哈希查找(超空间)
- 树上倍增
预处理
ancestor 数组记录了第 i 个 node 的倍增祖先,假设 i 为 100,即
ancestor[100][0] 记录了第 100 个 node 的第 1 个祖先
ancestor[100][1] 记录了第 100 个 node 的第 2 个祖先
ancestor[100][2] 记录了第 100 个 node 的第 4 个祖先
……
ancestor[100][j] 记录了第 100 个 node 的第 2j 个祖先
动态规划转移方程
ancestor[i][j] = ancestor[k][j-1], k = ancestor[i][j-1]
即当前节点的第 2j个祖先,是他的第 2j-1 个祖先的第 2j-1 个祖先
查询
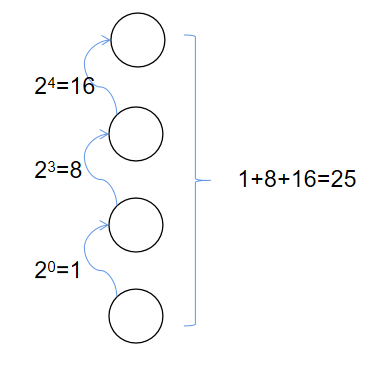
查询第 100 个 node 的第 k 个祖先节点,假设 k 为 25,即
k 的二进制表示为 11001,原查询可拆分为:
查询第 100 个 node
的第 20 个祖先节点
的第 23 个祖先节点
的第 24 个祖先节点
如下图:
参考代码(TS)
/**
* 3. 倍增
* 时间 O(nlogn + logk) 476ms 33%
* 空间 O(nlogn) 85.8mb 72%
*/
class TreeAncestor {
private level: number;
private ancestor: number[][];
/**
* 转移方程 ancestor[i][j] = ancestor[k][j-1], k = ancestor[i][j-1]
* i 的倍增层有没有父,有就跳到父的倍增层
* 当前节点的第 2^j 个祖先,是他的第 2^(j-1) 个祖先的第 2^(j-1) 个祖先
* 时间 O(nlogn)
* 空间 O(nlogn)
*/
constructor(n: number, parent: number[]) {
this.level = Math.ceil(Math.log2(n)); // log2(50000) = 16
this.ancestor = parent.map((pi) => {
const arr = new Array(this.level);
arr.fill(-1);
arr[0] = pi;
return arr;
});
for (let j = 1; j < this.level; j++) {
for (let i = 0; i < n; i++) {
const k = this.ancestor[i][j - 1];
if (k > -1) {
this.ancestor[i][j] = this.ancestor[k][j - 1];
}
}
}
}
/**
* 返回树节点的第 K 个祖先节点
* 时间 O(logk)
* 空间 O(1)
*/
getKthAncestor(node: number, k: number): number {
let _node = node;
for (let j = 0; j < this.level; j++) {
if (((k >> j) & 1) !== 0) {
_node = this.ancestor[_node][j];
if (_node === -1) return -1;
}
}
return _node === node ? -1 : _node;
}
}
其他相关:
BL(Binary Lifting)倍增法
ST(Sparse Table)稀疏表
LCA(Least Common Ancestors)最近公共祖先问题