文章目录
- ※ 参考资料
- 建立DH模型
- △ 基本概念和标准DH/改进DH
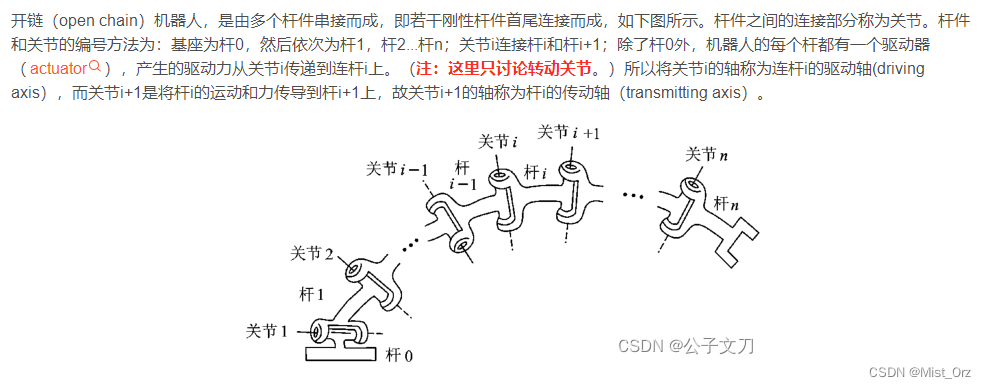
- ○ 连杆与关节的编号
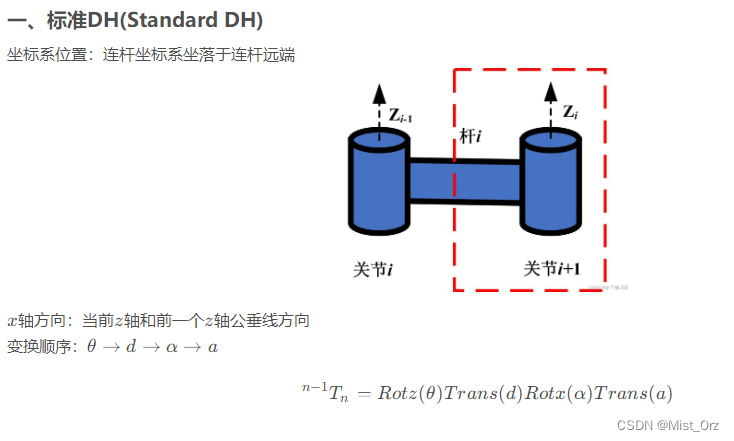
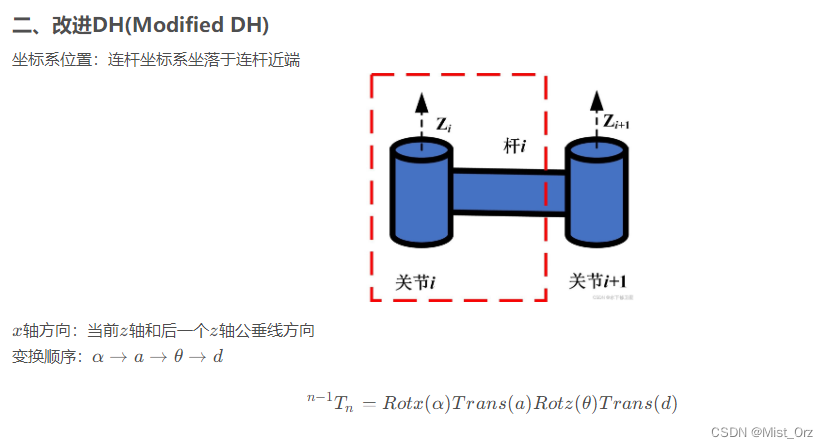
- ○ 标准DH与改进DH
- △ DH参数模型建立方法
- ○ 标准DH参数定义及方法简介
- · 连杆坐标系建立方法
- · 标准DH参数含义
- ※ 关于DH参数以哪个轴的指向为准的问题
- · 标准DH坐标系间的齐次变换矩阵
- ○ 改进DH参数定义及方法简介
- · 连杆坐标系建立方法
- · 改进DH参数含义
- · 改进DH坐标系间的齐次变换矩阵
- ※ 关于DH参数的作用
- △ ZK-500机器人DH建模过程及分析
- ○ 机器人尺寸参数
- ○ 标准DH(STD-DH)模型建立及验证
- · 标准DH模型建立过程
- · ZK-500机器人标准DH(STD-DH)参数
- · 验证标准DH模型参数
- ○ 改进DH(M-DH)模型建立过程及验证
- · 改进DH模型建立过程
- ※ 关于6杆的原点位置的选定
- · ZK-500机器人改进DH(M-DH)参数
- · 验证改进DH模型参数
关于机器人正逆解的原理、算法、代码什么的,在网上一找一大堆,其本身也是关于机器人的知识里面最基础的,其实没什么好写的,这里只是把我理解的内容整理一下,方便自己和需要的人查看。
另外这里要感谢赵而阳师弟,之前我在弄有限元分析的内容,把机器人相关的问题都丢给他了。
❤ 2023.6.6 ❤
※ 参考资料
关于机器人运动学的参考资料与文章挺多的,同时matlab实现机器人的正逆解有更简单的方法就是用“机器人工具箱(Robotics Toolbox)”,所以要说这里的资料是不是最好的最有价值的不一定,但至少有帮助吧。
首先是我之前整理的
→→→【Matlab机器人工具箱(Robotics Toolbox)学习笔记】
其实就是把B站一个将机器人工具箱的up的视频整理了一下,并且附上了自己的练习与验证内容
建立DH模型
这是由Danevit Harttnberg提出的故称为DH方法
关于机器人的DH建模的方法,在各种机器人参考书里都有,据说,外国的书用改进DH比较多,中国的书用标准DH比较多,其实我也没有仔细看过,但是根据我看过的书籍的内容,DH建模方法这部分都没有特别详细的讲解,可能是大家都觉得这个内容太基础了,没必要将这么详细吧。。。
总之,在最开始学习机器人时,大部分人对于该如何建立DH模型会感到很混乱,这里总结一下DH模型的建立方法。
首先是参考资料:
→→→【机器人标准DH建模与改进DH建模】
这篇文章用比较简练的语言和图形说明了标准DH和改进DH的区别
→→→【(3)机器人的DH参数建模详解】
这篇文章讲了我经常搞混的机器人关节和连杆的编号问题
△ 基本概念和标准DH/改进DH
○ 连杆与关节的编号
这里直接引用【(3)机器人的DH参数建模详解】中的内容
总结一下,就是从基座为0开始,第几个杆编号就是几,离基座近的一端的关节编号和杆相同,远的一端编号+1
○ 标准DH与改进DH
- 标准DH与改进DH建立方法的区别
这里引用【机器人标准DH建模与改进DH建模】:
总结一下:杆的坐标系建立在离底座远的一端的是标准DH,近的一端的是改进DH
- 标准DH与改进DH应用的区别
简单来说就是当一个关节连了两个杆的时候,标准DH会出现歧义,而改进DH不会
△ DH参数模型建立方法
这里主要引用
→→→【(3)机器人的DH参数建模详解】中的内容
原文里各种公式崩了,这里我用Latex重新整理了一下
○ 标准DH参数定义及方法简介
· 连杆坐标系建立方法
- 第一步:确定各坐标系的Z轴:
基本原则为:选取 z i z_{i} zi轴为关节i+1的轴向(如上面图片所示,如z1在轴2上)(指向可以任选,但是通常将各平行的Z轴的指向取为相同)。另外,机器人远端没有关节n+1,这时可以选取 z n z_{n} zn轴和 z n + 1 z_{n+1} zn+1轴重合 。
- 第二步:确定各坐标系的原点:
基本原则为:选取原点 o i o_{i} oi在过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴的公法线上(即公法线与 z i z_{i} zi轴的交点)。
注意:
① 当
z
i
−
1
z_{i-1}
zi−1轴和
z
i
z_{i}
zi轴平行时,两轴的公法线有无数条,若两轴重合则取
o
i
=
o
i
−
1
o_{i}=o_{i-1}
oi=oi−1,若两轴平行且不重合则过
o
i
−
1
o_{i-1}
oi−1点做两轴的公法线,此公法线与
z
i
z_{i}
zi轴的交点即为
o
i
o_{i}
oi。
② 由于没有
z
−
1
z_{-1}
z−1,故
o
0
o_{0}
o0的无法按上面的方法确定,若
z
0
z_{0}
z0与
z
1
z_{1}
z1相交则
o
0
=
o
1
o_{0}=o_{1}
o0=o1,若
z
0
z_{0}
z0与
z
1
z_{1}
z1不相交取
o
0
o_{0}
o0在
z
0
z_{0}
z0与
z
1
z_{1}
z1的公法线上。
- 第三步:确定各坐标系的X轴:
基本原则为:选取 x i x_{i} xi轴沿过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi 轴的公法线,方向从 z i − 1 z_{i-1} zi−1轴指向 z i z_{i} zi 轴。
注意:
① 当
z
i
−
1
z_{i-1}
zi−1轴与
z
i
z_{i}
zi 轴 重合时(这时
o
i
=
o
i
−
1
o_{i}=o_{i-1}
oi=oi−1),选取
x
i
x_{i}
xi轴满足在初始位置时
x
i
x_{i}
xi轴与
x
i
−
1
x_{i-1}
xi−1轴重合。
② 当
z
i
−
1
z_{i-1}
zi−1轴与
z
i
z_{i}
zi 轴相交且不重合时,选择
x
i
=
±
(
z
i
−
1
×
z
i
)
x_{i}=\pm (z_{i-1} \times z_{i})
xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
③ 当i=0时,由于
o
0
=
o
1
o_{0}=o_{1}
o0=o1或
o
0
o_{0}
o0在
z
0
z_{0}
z0与
z
1
z_{1}
z1的公法线上,选取在初始位置时
x
0
x_{0}
x0轴与
x
1
x_{1}
x1轴重合。
- 第四步:确定各坐标系的Y轴:
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
· 标准DH参数含义
1、杆件长度 a i a_{i} ai:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i x_{i} xi轴的指向为正;
2、杆件扭角 α i \alpha_{i} αi:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i x_{i} xi轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in(-\pi,\pi] αi∈(−π,π];
3、关节距离 d i d_{i} di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i − 1 z_{i-1} zi−1轴的指向为正;
4、关节扭角 θ i \theta_{i} θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i − 1 z_{i-1} zi−1轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi,\pi] θi∈(−π,π];
※ 关于DH参数以哪个轴的指向为准的问题
这个问题我开始有点乱,为什么 a i a_{i} ai是以 x i x_{i} xi轴的指向为正而不是 x i − 1 x_{i-1} xi−1,而 d i d_{i} di就是以 z i − 1 z_{i-1} zi−1轴的指向为正而不是 z i z_{i} zi呢?
我想考了一下,我觉得这个是根据前面的建立各连杆的坐标系的方法决定的,其实抛开这些概念,将坐标系标在机器人结构图上就明白了,比如 a i a_{i} ai表示的是连杆长,也就是z轴间的距离,只有 x i x_{i} xi的方向才能表示出从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi的长度,于是才选定 x i x_{i} xi的方向为正。 d i d_{i} di同理
【!】这是我的理解,不知道是不是正确
· 标准DH坐标系间的齐次变换矩阵
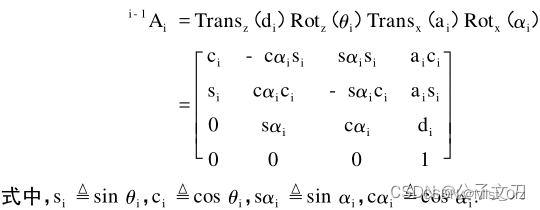
○ 改进DH参数定义及方法简介
· 连杆坐标系建立方法
- 第一步:确定各坐标系的Z轴:
基本原则为:选取 z i z_{i} zi轴为关节 i i i的轴向 。
- 第二步:确定各坐标系的原点:
基本原则为:选取原点 o i o_{i} oi在过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线上。
注意:
当
z
i
z_{i}
zi轴和
z
i
+
1
z_{i+1}
zi+1轴平行时,两轴的公法线有无数条,若两轴重合则取
o
i
=
o
i
−
1
o_{i}=o_{i-1}
oi=oi−1(【???】这里存疑,我是按照标准DH写的),若两轴平行且不重合则过
o
i
−
1
o_{i-1}
oi−1点做两轴的公法线,此公法线与
z
i
z_{i}
zi轴的交点即为
o
i
o_{i}
oi。
- 第三步:确定各坐标系的X轴:
基本原则为:选取 x i x_{i} xi轴沿过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线,方向从 z i z_{i} zi轴指向 z i + 1 z_{i+1} zi+1轴。
注意:
① 当
z
i
z_{i}
zi轴与
z
i
+
1
z_{i+1}
zi+1 轴 重合时(这时
o
i
=
o
i
−
1
o_{i}=o_{i-1}
oi=oi−1),选取
x
i
x_{i}
xi轴满足在初始位置时
x
i
x_{i}
xi轴与
x
i
−
1
x_{i-1}
xi−1轴重合。(【!!!】存疑,我是按照标准DH写的)
② 当
z
i
−
1
z_{i-1}
zi−1轴与
z
i
z_{i}
zi 轴相交且不重合时,选择
x
i
=
±
(
z
i
−
1
×
z
i
)
x_{i}=\pm (z_{i-1} \times z_{i})
xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
- 第四步:确定各坐标系的Y轴:
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
· 改进DH参数含义
1、杆件长度 a i − 1 a_{i-1} ai−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i − 1 x_{i-1} xi−1轴的指向为正;
2、杆件扭角 α i − 1 \alpha_{i-1} αi−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i − 1 x_{i-1} xi−1轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in (-\pi ,\pi ] αi∈(−π,π];
3、关节距离 d i d_i di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i z_{i} zi轴的指向为正;
4、关节扭角 θ i \theta_i θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i z_{i} zi轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi ,\pi ] θi∈(−π,π];
※ 关于这里为什么是 a i − 1 a_{i-1} ai−1与 α i − 1 \alpha_{i-1} αi−1
我的理解是,DH参数的作用是描述第 i {i} i个连杆的起始位置的参数,由于改进DH的坐标是建立在连杆的前端,也就是驱动轴上,那么能描述第 i {i} i个连杆的参数也就是该连杆的驱动轴与传动轴的距离(或者说关节偏置) d i d_i di(对于转动关节来说),以及第 i {i} i个连杆与第 i − 1 {i-1} i−1个连杆的相对位置的参数就是第 i − 1 {i-1} i−1个连杆的长度 a i − 1 a_{i-1} ai−1和夹角 α i − 1 \alpha_{i-1} αi−1。
如【机械臂运动学教程】机械臂+旋转矩阵+变换矩阵+DH+逆解+轨迹规划+机器人+教程视频中所示

其实在用改进DH(M-DH)建立机器人模型时不需要考虑那么多,只要把连杆对应的这一行参数填进去就行。
· 改进DH坐标系间的齐次变换矩阵
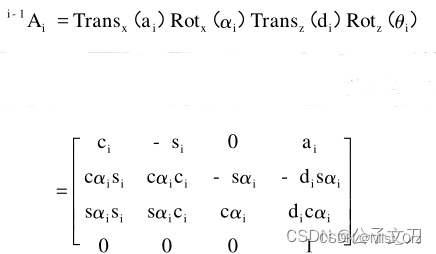
※ 关于DH参数的作用
为什么需要四个DH参数,刚开始我还不太懂,后来看了这个视频,老师讲的很明白
→→→【【机械臂运动学教程】机械臂+旋转矩阵+变换矩阵+DH+逆解+轨迹规划+机器人+教程】
P4 4.机械臂几何法与DH表示法
用 a a a和 α \alpha α可以表示出同一个杆的驱动轴和传动轴之间的变化关系
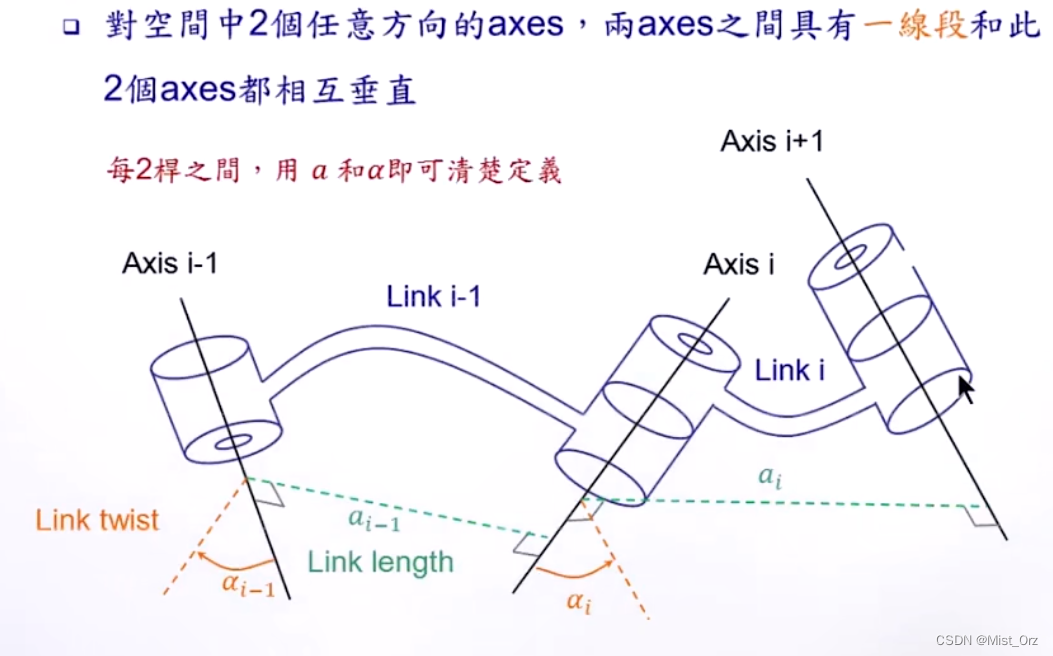
当有多个杆件串联时,需要 d d d和 θ \theta θ来表示两个杆件之间的相对位置关系
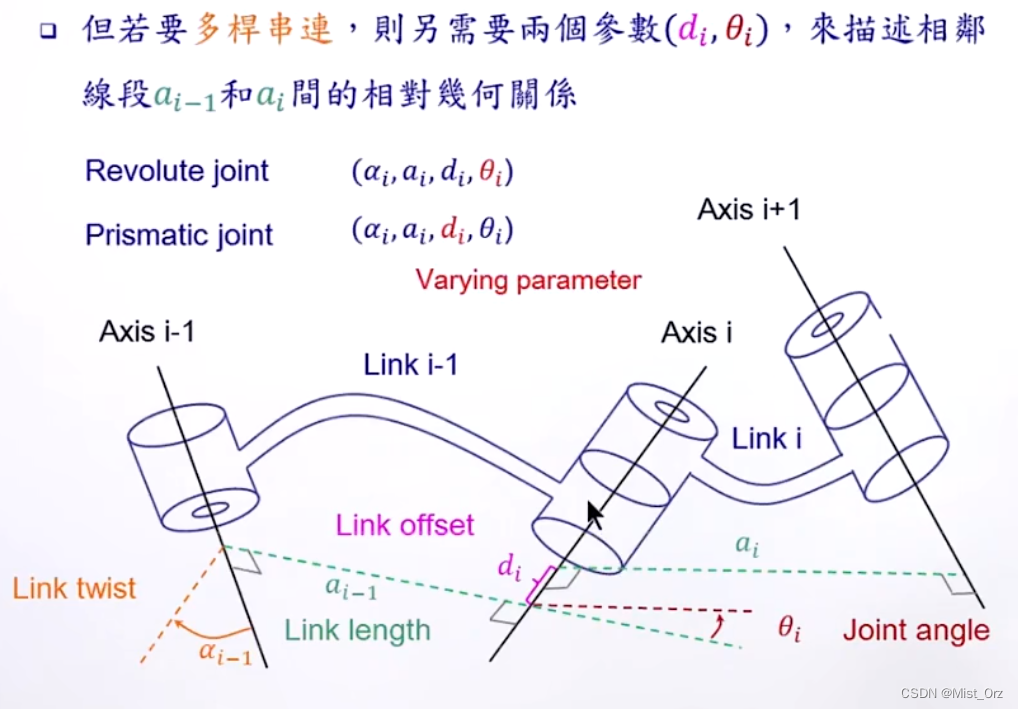
其中,在旋转关节中, θ \theta θ是变量,在平移关节中, d d d是变量
△ ZK-500机器人DH建模过程及分析
○ 机器人尺寸参数
这个机器人时南通振康生产的500Kg重载机器人(国产哦),现在用来做机器人搅拌摩擦焊的实验

- 机器人的尺寸及工作范围如下
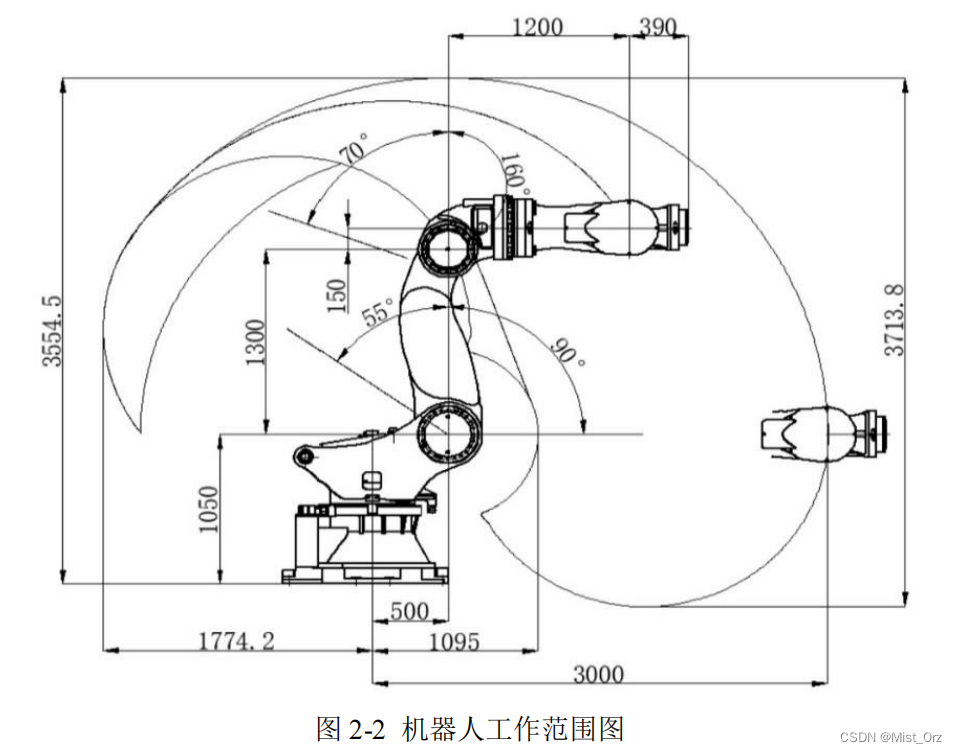
○ 标准DH(STD-DH)模型建立及验证
关于工业机器人标准DH(STD-DH)建模的参考结果可以见这篇文章
→→→【工业六轴机器人常见的STD(标准)-DH模型建立方法】
只是他的方法和我的z轴的方向不同
同时标准DH的正逆解验证也可以参考同一个作者的这篇文章
→→→【SD-H模型运动学正解、逆解及姿态角的解算验证】
· 标准DH模型建立过程
- 确定z轴方向
基本原则为:选取 z i z_{i} zi轴为关节i+1的轴向(如上面图片所示,如z1在轴2上)(指向可以任选,但是通常将各平行的Z轴的指向取为相同)。另外,机器人远端没有关节n+1,这时可以选取 z n z_{n} zn轴和 z n + 1 z_{n+1} zn+1轴重合 。
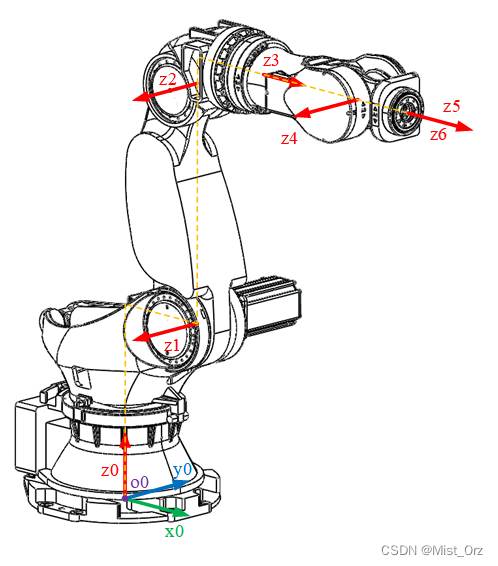
- 确定原点位置
基本原则为:选取原点 o i o_{i} oi在过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴的公法线上(即公法线与 z i z_{i} zi轴的交点)。
注意:
① 当 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴平行时,两轴的公法线有无数条,若两轴重合则取 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1,若两轴平行且不重合则过 o i − 1 o_{i-1} oi−1点做两轴的公法线,此公法线与 z i z_{i} zi轴的交点即为 o i o_{i} oi。
② 由于没有 z − 1 z_{-1} z−1,故 o 0 o_{0} o0的无法按上面的方法确定,若 z 0 z_{0} z0与 z 1 z_{1} z1相交则 o 0 = o 1 o_{0}=o_{1} o0=o1,若 z 0 z_{0} z0与 z 1 z_{1} z1不相交取 o 0 o_{0} o0在 z 0 z_{0} z0与 z 1 z_{1} z1的公法线上。
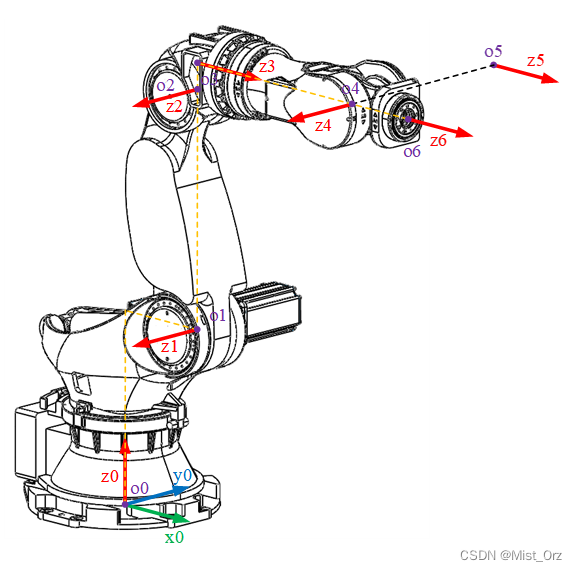
- 确定x轴方向
基本原则为:选取 x i x_{i} xi轴沿过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi 轴的公法线,方向从 z i − 1 z_{i-1} zi−1轴指向 z i z_{i} zi 轴。
注意:
① 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴 重合时(这时 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1),选取 x i x_{i} xi轴满足在初始位置时 x i x_{i} xi轴与 x i − 1 x_{i-1} xi−1轴重合。
② 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴相交且不重合时,选择 x i = ± ( z i − 1 × z i ) x_{i}=\pm (z_{i-1} \times z_{i}) xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
③ 当i=0时,由于 o 0 = o 1 o_{0}=o_{1} o0=o1或 o 0 o_{0} o0在 z 0 z_{0} z0与 z 1 z_{1} z1的公法线上,选取在初始位置时 x 0 x_{0} x0轴与 x 1 x_{1} x1轴重合。
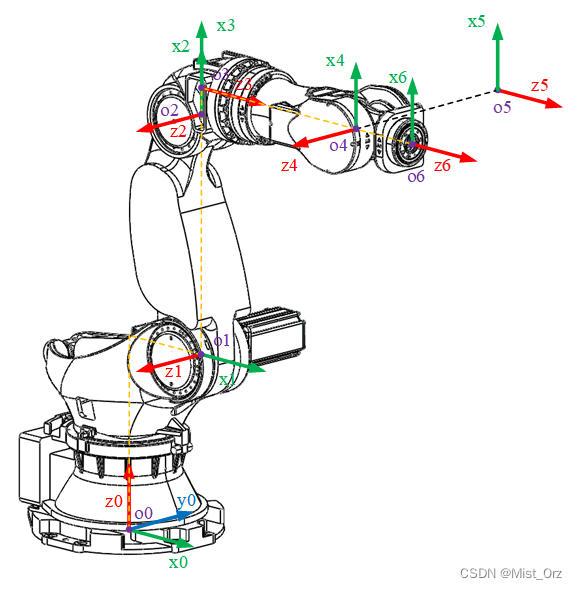
- 确定y轴方向
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
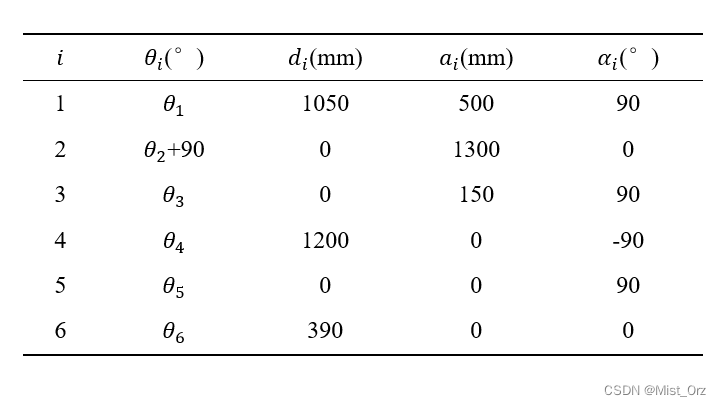
· ZK-500机器人标准DH(STD-DH)参数
1、杆件长度 a i a_{i} ai:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i x_{i} xi轴的指向为正;
2、杆件扭角 α i \alpha_{i} αi:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i x_{i} xi轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in(-\pi,\pi] αi∈(−π,π];
3、关节距离 d i d_{i} di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i − 1 z_{i-1} zi−1轴的指向为正;
4、关节扭角 θ i \theta_{i} θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i − 1 z_{i-1} zi−1轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi,\pi] θi∈(−π,π];
· 验证标准DH模型参数
使用matlab机器人工具箱验证标准DH模型
建立机器人模型
d1=1050;a1=500;a2=1300;a3=150;d4=1200;d6=390;
% theta(z) d(z) a(x) alpha(x)
L1=Link([ 0 d1 a1 pi/2 ],'standard');
L2=Link([ 0 0 a2 0 ],'standard');L2.offset=pi/2;
L3=Link([ 0 0 a3 pi/2 ],'standard');
L4=Link([ 0 d4 0 -pi/2 ],'standard');
L5=Link([ 0 0 0 pi/2 ],'standard');
L6=Link([ 0 d6 0 0 ],'standard');
Robot_6=SerialLink([L1,L2,L3,L4,L5,L6],'name','ZK-500');
Robot_6.teach;
注意这里的
L2.offset=pi/2;,是对应连杆2的90°的补偿,
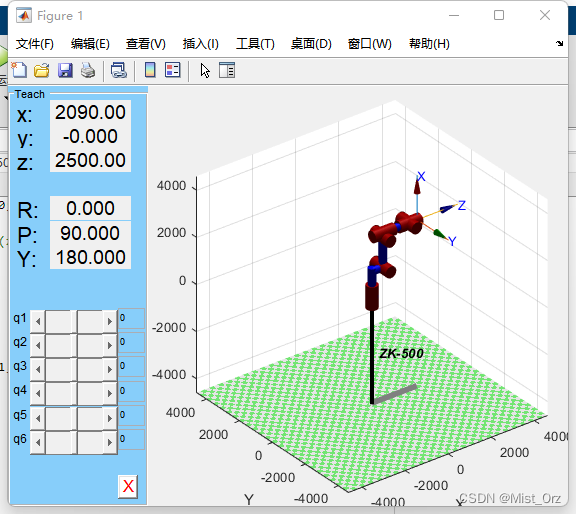
运行结果
○ 改进DH(M-DH)模型建立过程及验证
关于工业机器人标准DH(STD-DH)建模的参考结果可以见这篇文章(和上面那篇同一个作者)
→→→【工业六轴机器人常见的MOD(改进)-DH模型建立方法】
只是他的方法和我的z轴的方向不同
同时改进DH的正逆解验证也可以参考同一个作者的这篇文章
→→→【MD-H模型运动学正解、逆解及姿态角的解算验证】
· 改进DH模型建立过程
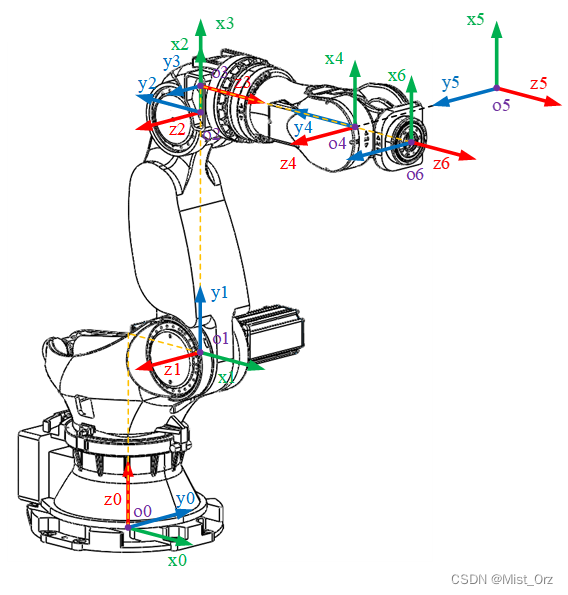
- 确定z轴方向
根据原则,选取 z i z_{i} zi轴为关节 i i i的轴向 。
确定各关节z轴方向如图所示:
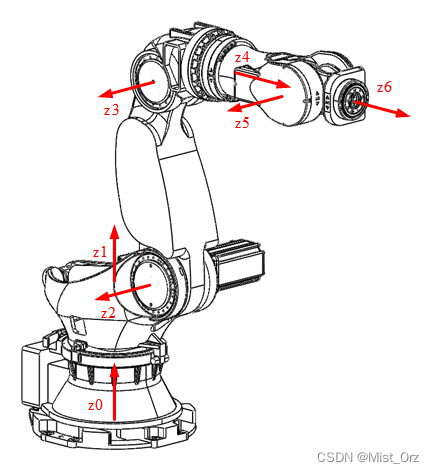
关于z轴方向的问题,理论上来说都可以,但是我看有的教程说要按照轴旋转的方向确定z轴的朝向,为此我还特地去查看了下机器人的各轴实际转动方向,但是转念一想,旋转方向如果实际和坐标不一致,那么只要在带入求解的时候加个负号就行了,但是如果在建立DH模型时就考虑方向,那么模型的通用型就会受到限制。
于是我决定按照:轴向沿竖直方向的轴(如1轴)方向向上,轴向沿水平方向的轴(如2、3、5轴)方向向外,轴向指向末端的轴(如4、6轴)方向指向末端的习惯来确定z轴的朝向。
- 确定原点位置
基本原则为:选取原点 o i o_{i} oi在过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线上。
注意:
当 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴平行时,两轴的公法线有无数条,若两轴重合则取 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1(【!!!】存疑),若两轴平行且不重合则过 o i − 1 o_{i-1} oi−1点做两轴的公法线,此公法线与 z i z_{i} zi轴的交点即为 o i o_{i} oi。
按照以上原则,标注各连杆坐标系原点如图并适当平移了z轴的位置:
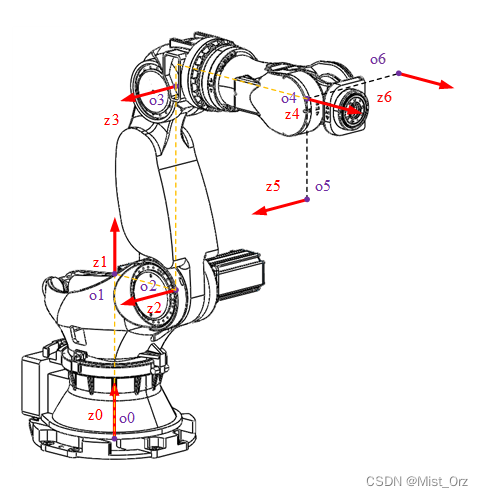
连杆4、5、6的坐标系的原点在同一个点,这里将5、6杆坐标系平移到不重叠的位置。
※ 关于6杆的原点位置的选定
按照传统的标准DH和改进DH模型,6杆的坐标原点都是应该建在机器人末端6轴的轴线位置的,但是如果将6杆的坐标原点移动到和4、5杆重合的位置,同时建立一个工具坐标系,将6杆的长度算作工具长度的一部分,则会大大简化逆解运算的复杂程度(听我师弟说的)。
原因我后面再讲(如果我写到后面能记起来的话。。。)
- 确定x轴方向
基本原则为:选取 x i x_{i} xi轴沿过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线,方向从 z i z_{i} zi轴指向 z i + 1 z_{i+1} zi+1轴。
注意:
① 当 z i z_{i} zi轴与 z i + 1 z_{i+1} zi+1 轴 重合时(这时 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1),选取 x i x_{i} xi轴满足在初始位置时 x i x_{i} xi轴与 x i − 1 x_{i-1} xi−1轴重合。(【!!!】存疑)
② 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴相交且不重合时,选择 x i = ± ( z i − 1 × z i ) x_{i}=\pm (z_{i-1} \times z_{i}) xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
顺便标上了基座坐标系和工具坐标系
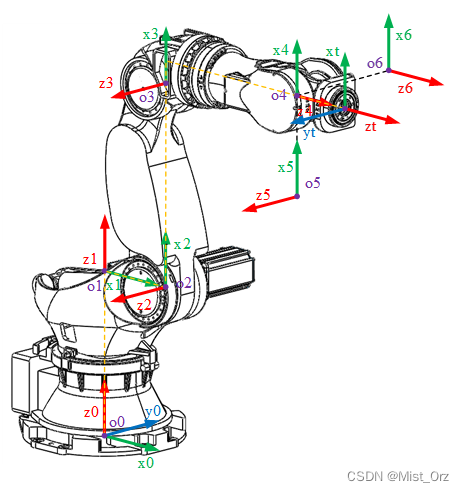
- 确定y轴方向
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
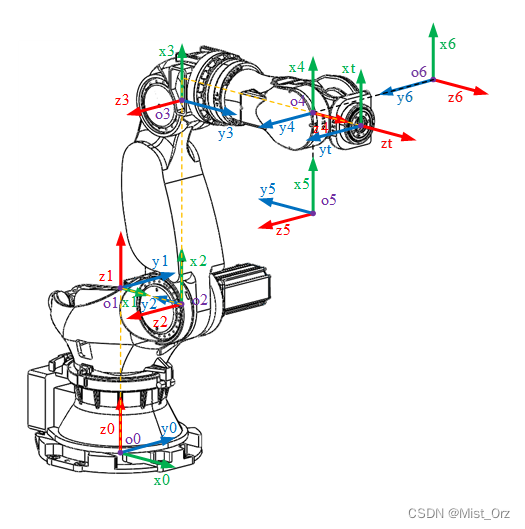
完成!
然后和大佬做的比较一下(其实我就是一边比较一边做的。。。)

简直一模一样
· ZK-500机器人改进DH(M-DH)参数
1、杆件长度 a i − 1 a_{i-1} ai−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i − 1 x_{i-1} xi−1轴的指向为正;
2、杆件扭角 α i − 1 \alpha_{i-1} αi−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i − 1 x_{i-1} xi−1轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in (-\pi ,\pi ] αi∈(−π,π];
3、关节距离 d i d_i di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i z_{i} zi轴的指向为正;
4、关节扭角 θ i \theta_i θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i z_{i} zi轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi ,\pi ] θi∈(−π,π];
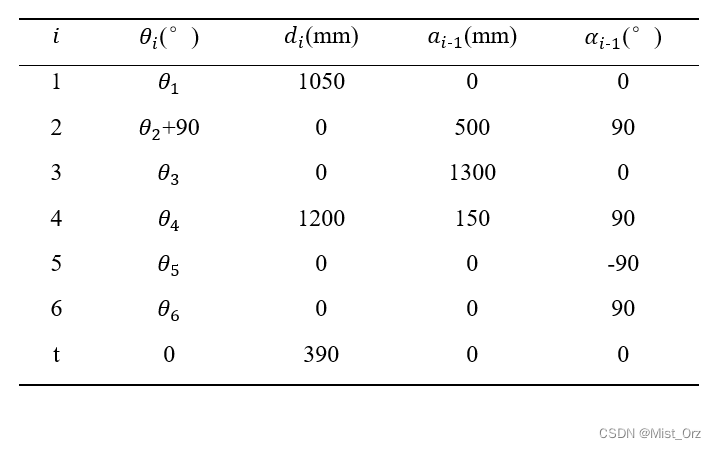
· 验证改进DH模型参数
使用matlab机器人工具箱验证改进DH模型
建立机器人模型
d1=1050;a1=500;a2=1300;a3=150;d4=1200;d6=390;
% theta(z) d(z) a(x) alpha(x)
L1=Link([ 0 d1 0 0 ],'modified');
L2=Link([ 0 0 a1 pi/2 ],'modified');L2.offset=pi/2;
L3=Link([ 0 0 a2 0 ],'modified');
L4=Link([ 0 d4 a3 pi/2 ],'modified');
L5=Link([ 0 0 0 -pi/2 ],'modified');
L6=Link([ 0 d6 0 pi/2 ],'modified');
Robot_6=SerialLink([L1,L2,L3,L4,L5,L6],'name','ZK-500');
Robot_6.teach;
这里没有完全按照上面的表格来配置参数,也就是没有将杆6的偏置作为工具的长度,而是按照一般的方法将其带入了杆6的参数
结果如下
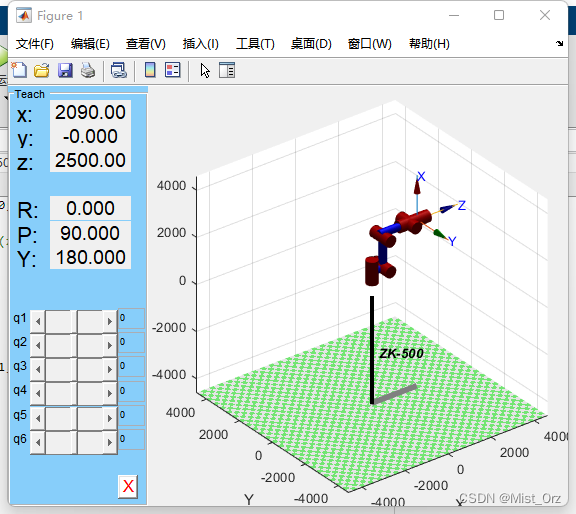
虽然长得有点奇怪,但是拖动了一下各个轴,结果还是比较正常的。
OK,至此完成了ZK-500机器人的DH建模