努力是为了不平庸~
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。
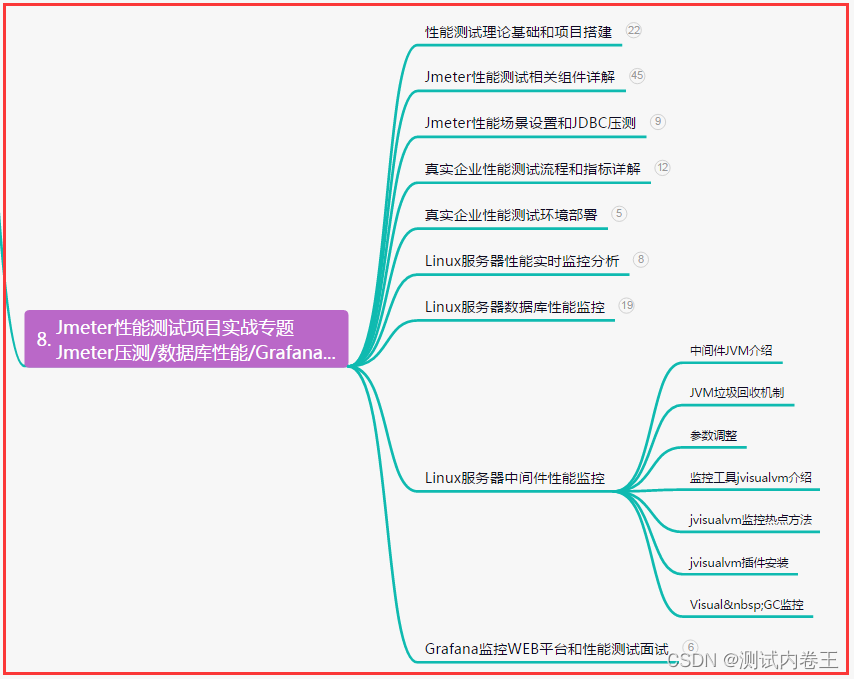
目录
一、引言
二、思路
1. 确定问题和目标:
2. 确定算法和数据结构:
3. 编写代码框架
4. 实现辅助函数:
5. 实现主函数:
6. 实现搜索算法:
7. 实现状态操作函数:
8. 进行测试和调试:
三、代码与函数
A、代码步骤的方法、目的及意义
①导入必要的库:
②定义open表与close表以及初始状态和目标状态:
③定义节点类:
④定义辅助函数,实现节点类:
⑤定义函数get_reverse_num(state)用于计算逆序数,判断解的存在性。
⑥定义函数display(cur_node)用于输出状态及深度信息。
⑦定义函数is_in_list(alist, state)用于检查状态是否在列表中。
⑧定义排序的权值函数delta(node)。
⑨输入初始状态和目标状态:
⑩判断是否存在可行解:
⑪启发式搜索的实现:
B、函数构造和作用
1. 函数get_reverse_num(state):
2. 函数display(cur_node):
3. 函数is_in_list(alist, state):
4. 函数delta(node):
四、state和parent的属性和作用
1.state属性:
2. parent属性:
五、解题代码
一、引言
A*算法是一种启发式图搜索算法,其特点在于对估价函数的定义上。对于一般的启发式图搜索,总是选择估价函数f值最小的节点作为扩展节点。因此,f是根据需要找到一条最小代价路径的观点来估算节点的,所以,可考虑每个节点n的估价函数值为两个分量:从起始节点到节点n的实际代价以及从节点n到达目标节点的估价代价。
以8数码问题为例实现A*算法的求解程序。

估价函数f(n) = g(n) + h(n)
g(n)=d(n)——结点n在搜索树中的深度
h(n)可选择h1(n)——结点n中“不在位”的数码个数 或 h2(n) =p(n)= 将牌“不在位”的距离和
二、思路
1. 确定问题和目标:
八数码问题,即通过移动数字将初始状态转变为目标状态。目标是编写能够自动求解八数码问题的程序。
2. 确定算法和数据结构:
选择A*算法,然后确定所需的数据结构,如节点类、状态表示方法等。
3. 编写代码框架
①定义必要的变量和数据结构,如open表、close表、初始状态和目标状态等。
②创建节点类,并定义节点类的属性和方法。
4. 实现辅助函数:
根据代码中的需要,实现辅助函数,如find_pos函数用于找到数字在状态中的位置。
5. 实现主函数:
①编写主函数,处理用户输入和输出。
②获取用户输入的初始状态和目标状态。
③检查可行解的存在性,判断是否可以通过移动数字从初始状态到达目标状态。
④如果可行解存在,开始启发式搜索过程。
6. 实现搜索算法:
①在主函数中编写启发式搜索的逻辑。
②创建open表和close表,并初始化。
③使用循环迭代进行搜索,直到找到可行解或无解。
④在每次迭代中,根据算法规则进行状态扩展和判断,并更新open表和close表。
7. 实现状态操作函数:
根据算法需求,实现状态操作函数,如移动空白格、判断状态是否在表中等。
8. 进行测试和调试:
①编写测试用例,包括不同的初始状态和目标状态。
②运行代码,并观察输出结果是否符合预期。
③根据需要进行调试和修正代码错误。
三、代码与函数
A、代码步骤的方法、目的及意义
①导入必要的库:
这里使用了NumPy库,它提供了Python中对多维数组进行高效操作的功能。
②定义open表与close表以及初始状态和目标状态:
open表用于存放待扩展的节点,close表用于存放已扩展的节点。start_state和target_state分别表示初始状态和目标状态,都是3x3的二维数组。
③定义节点类:
这里定义了一个名为Node的类,表示搜索过程中的节点。该类具有一些属性和方法,用于存储节点状态、计算代价等信息。
④定义辅助函数,实现节点类:
find_pos(self, state, num):在状态state中查找值为num的元素的位置。
__init__(self, state, prt=[]):节点类的构造函数,初始化节点的状态、父节点、代价等信息。
moveto(self, x, y):将空白格移动到指定位置(x, y),生成新的状态。
⑤定义函数get_reverse_num(state)用于计算逆序数,判断解的存在性。
意义:逆序数用于判断八数码问题是否有可行解。
⑥定义函数display(cur_node)用于输出状态及深度信息。
意义:用于展示搜索过程中每个节点的状态、搜索深度、代价等信息。
⑦定义函数is_in_list(alist, state)用于检查状态是否在列表中。
意义:用于判断一个状态是否已经在open表或close表中。
⑧定义排序的权值函数delta(node)。
意义:用于指定节点的排序权值,这里使用节点的F值作为排序依据。
⑨输入初始状态和目标状态:
意义:使用输入函数逐个获取用户输入的初始状态和目标状态。
⑩判断是否存在可行解:
使用逆序数判断八数码问题是否有可行解。如果逆序数的奇偶性不同,则不存在可行解。
⑪启发式搜索的实现:
在启发式搜索中,使用open表存放待扩展的节点,close表存放已扩展的节点。通过不断扩展节点,并将其加入open表和close表,最终找到可行解。搜索过程中,使用delta函数对open表中的节点按照F值进行排序
以上是对代码的关键步骤的分析。
B、函数构造和作用
1. 函数get_reverse_num(state):
构成:
①参数:state,表示一个状态的二维数组。
②返回值:逆序数,表示状态中元素的逆序对数量。
作用:该函数用于计算逆序数,判断八数码问题是否有可行解。通过将非空元素按顺序拼接成字符串s,然后统计在s中出现的逆序对数量,最终得到逆序数。
2. 函数display(cur_node):
构成:
①参数:cur_node,表示当前节点对象。
②作用:该函数用于展示搜索过程中每个节点的状态、搜索深度、代价等信息。首先,它通过跟踪节点的父节点,将搜索路径中的所有节点存储在列表alist中。然后,它按照搜索路径的顺序遍历alist,打印每个节点的搜索深度G、状态state、代价信息G、H、F。
3. 函数is_in_list(alist, state):
构成:
①参数:alist,表示一个节点列表;state,表示一个状态的二维数组。
②返回值:如果状态state在列表alist中存在,则返回对应的节点对象;否则返回-1。
作用:该函数用于判断一个状态是否已经在open表或close表中。它遍历列表alist中的节点对象,将每个节点的状态与输入的state进行比较。如果找到匹配的状态,则返回对应的节点对象;否则返回-1,表示状态不在列表中。
4. 函数delta(node):
构成:
①参数:node,表示一个节点对象。
②返回值:节点的代价F。
作用:该函数用于作为排序的权值函数。在启发式搜索中,根据节点的代价F值对open表中的节点进行排序。
四、state和parent的属性和作用
state和parent是节点类中的两个重要属性
1.state属性:
构成:state是一个二维数组,表示节点对应的状态。
作用:state记录当前节点状态,即一个具体的排列。通过不同的状态组合,可以表示不同的八数码棋盘布局。
例:在代码中的使用:通过current_node.state可以获取当前节点的状态。
2. parent属性:
构成:parent是一个列表,存储指向父节点的引用。
作用:parent记录了当前节点的父节点,即在搜索树中指向当前节点的上一层节点。
例:在代码中的使用:通过current_node.parent可以获取当前节点的父节点。这对于回溯搜索路径和展示解决方案非常有用,因为可以通过跟踪父节点,从目标节点一直追溯到初始节点,形成搜索路径。
在启发式搜索中,每个节点都通过移动空白格生成新的状态,并将其作为子节点添加到搜索树中。通过state和parent属性的设置和更新,可以构建搜索树,跟踪搜索路径,并最终找到解决八数码问题的路径。
五、解题代码
import numpy as np
# 定义open表与close表
open_list = [] # 存放待扩展的节点
close_list = [] # 存放已扩展的节点
start_state = np.zeros((3, 3), dtype=int) # 初始状态,3×3矩阵,先全设为零
target_state = np.zeros((3, 3), dtype=int) # 目标状态,3×3矩阵,先全设为零
# 定义节点类
# 定义了一个名为Node的类,表示搜索过程中的节点。该类具有一些属性和方法,用于存储节点状态、计算代价等信息。
class Node:
G = 0 # 起点到当前节点的最短路径代价值
H = 0 # 当前节点到目标节点的最短路径代价值
F = 0 # F = G + H,起点经过当前节点到目标节点的最短路径的总代价值
state = np.zeros((3, 3), dtype=int) # 一个二维数组,记录了当前节点的状态,即八数码问题中的一个具体排列。通过不同的状态组合,可以表示不同的八数码棋盘布局。
parent = [] # 一个列表,记录了当前节点的父节点,即在搜索树中指向当前节点的上一层节点。
#find_pos(self, state, num)是节点类中的一个方法,用于找到指定数字在状态中的位置
# self:表示节点对象自身。 state:表示一个状态的二维数组。 num:表示要查找的数字。 返回一个包含两个元素的元组(i, j),表示数字num在状态state中的行索引和列索引。
def find_pos(self, state, num): # 在状态state中查找值为num的元素的位置x,y
for i in range(len(state)):
for j in range(len(state[i])):
if state[i][j] == num:
return i, j
# 节点类的构造函数,初始化节点的状态、父节点、代价等信息。
def __init__(self, state, prt=[]):
self.state = state
if prt:
self.parent = prt
self.G = prt.G + 1
for i in range(len(state)):
for j in range(len(state[i])):
x, y = self.find_pos(target_state, state[i][j])
self.H = self.H + abs(x - i) + abs(y - j)
self.F = self.G * 1 + self.H * 10
# 将空白格移动到指定位置(x, y),生成新的状态。
def moveto(self, x, y):
x0, y0 = self.find_pos(self.state, 0)
newstate = self.state.copy()
tmp = newstate[x0][y0]
newstate[x0][y0] = newstate[x][y]
newstate[x][y] = tmp
return newstate
# 得到逆序数,用于判断解的存在性
# 逆序数用于判断八数码问题是否有可行解
def get_reverse_num(state):
ans = 0
s = ""
for i in range(len(state)):
for j in range(len(state[i])):
if not state[i][j] == 0:
s += str(state[i][j])
for i in range(len(s)):
for j in range(i):
if s[j] > s[i]:
ans += 1
return ans
# 输出状态及深度信息
# 用于展示搜索过程中每个节点的状态、搜索深度、代价等信息
def display(cur_node):
alist = []
tmp = cur_node
while tmp:
alist.append(tmp)
tmp = tmp.parent
alist.reverse()
for node in alist:
print("搜索深度%d" % node.G)
print(node.state)
print("G={0},H={1},F={2}".format(node.G, node.H, node.F))
print()
print("总共探索了%d次" % int(node.G + 1))
# 检查state状态是否在list中(可能是open或close表)
# 用于判断一个状态是否已经在open表或close表中
def is_in_list(alist, state):
for stat in alist:
if (stat.state == state).all():
return stat
return -1
# 排序的权值函数
# 用于指定节点的排序权值,这里使用节点的F值作为排序依据
def delta(node):
return node.F
# 输入初始与目标状态
# 使用输入函数逐个获取用户输入的初始状态和目标状态
for i in range(len(start_state)):
for j in range(len(start_state[i])):
start_state[i][j] = input("start_state" + "(" + str(i + 1) + "," + str(j + 1) + "):")
print("the start state is:")
print(start_state)
for i in range(len(target_state)):
for j in range(len(target_state)):
target_state[i][j] = input("target_state" + "(" + str(i + 1) + "," + str(j + 1) + "):")
print("the target state is:")
print(target_state)
# 可行解判断
# 使用逆序数判断八数码问题是否有可行解。如果逆序数的奇偶性不同,则不存在可行解
if get_reverse_num(target_state) % 2 != get_reverse_num(start_state) % 2:
print(get_reverse_num(target_state))
print(get_reverse_num(start_state))
print("找不到可行解!")
exit(-1)
# 可行解存在时,开始启发搜索
# 在启发式搜索中,使用open表存放待扩展的节点,close表存放已扩展的节点。
# 通过不断扩展节点,并将其加入open表和close表,最终找到可行解。搜索过程中,使用delta函数对open表中的节点按照F值进行排序
open_list.append(Node(start_state))
while open_list:
current_node = open_list.pop(0) # 从open表中取出F值最小的节点进行扩展
close_list.append(current_node) # 将扩展的节点加入close表
# 当open表中取出的恰好为目标状态时,找到可行解
if (current_node.state == target_state).all():
print("可行解已找到!")
display(current_node)
exit(0)
# 否则对当前节点进行拓展
x, y = current_node.find_pos(current_node.state, 0) # 找到空白格的位置
for [x_, y_] in [[x + 1, y], [x - 1, y], [x, y + 1], [x, y - 1]]:
if 0 <= x_ < len(start_state) and 0 <= y_ < len(start_state):
new_state = current_node.moveto(x_, y_) # 移动空白格得到新状态
# 判断新状态是否在close表
if is_in_list(close_list, new_state) == -1:
# 如果不在close表
if is_in_list(open_list, new_state) == -1:
# 如果也不在open表,则将其加入open表
open_list.append(Node(new_state, current_node))
else:
# 如果open表中已存在这种状态,则选取G值较小的
index = is_in_list(open_list, new_state)
if current_node.G + 1 < open_list[index].G:
# 如果新路线更好,则放弃旧路线而选择新路线
open_list.pop(index)
open_list.append(Node(new_state, current_node))
# 否则忽略
# 对open表按F值从小到大进行排序
open_list.sort(key=delta)





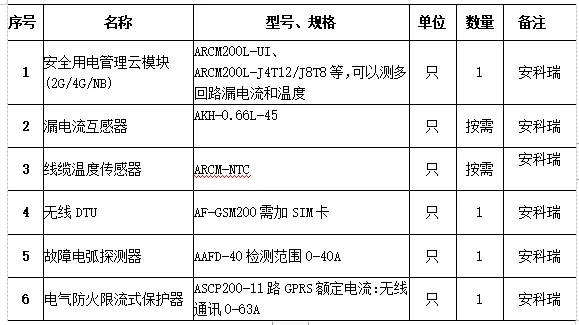



![千万级入口服务[Gateway]框架设计(一)](https://img-blog.csdnimg.cn/e5220fc8d4844163b92429ee98a58fba.png)