分类目录：《深入理解深度学习》总目录

相关文章：
·注意力机制（AttentionMechanism）：基础知识
·注意力机制（AttentionMechanism）：注意力汇聚与Nadaraya-Watson核回归
·注意力机制（AttentionMechanism）：注意力评分函数（AttentionScoringFunction）
·注意力机制（AttentionMechanism）：Bahdanau注意力
·注意力机制（AttentionMechanism）：多头注意力（MultiheadAttention）
·注意力机制（AttentionMechanism）：自注意力（Self-attention）
·注意力机制（AttentionMechanism）：位置编码（PositionalEncoding）

---

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为， 然后将不同的行为作为知识组合起来， 捕获序列内各种范围的依赖关系 （例如，短距离依赖和长距离依赖关系）。因此，允许注意力机制组合使用查询、键和值的不同子空间表示（Representation Subspaces）可能是有益的。

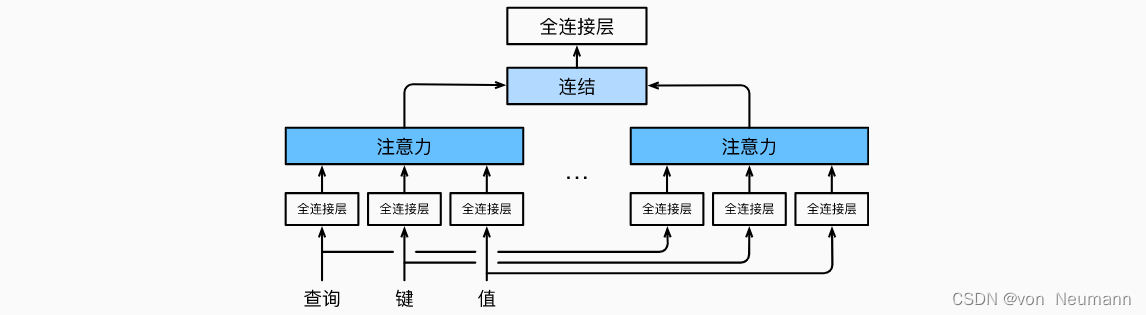
为此，与其只使用单独一个注意力汇聚， 我们可以用独立学习得到的组不同的线性投影（Linear Projections）来变换查询、键和值。 然后，这组变换后的查询、键和值将并行地送到注意力汇聚中。 最后，将这个注意力汇聚的输出拼接在一起， 并且通过另一个可以学习的线性投影进行变换， 以产生最终输出。 这种设计被称为多头注意力（Multihead Attention）。对于个注意力汇聚输出，每一个注意力汇聚都被称作一个头（Head）。 下图展示了使用全连接层来实现可学习的线性变换的多头注意力：

给定查询$q\in R^{d_q}$、 键$k\in R^{d_k}$和值$v\in R^{d_v}$， 每个注意力头$h_i(i=1,2,\cdots ,h)$的计算方法为：
$$h_i=f(W_i^{q}q,W_i^{k}k,W_i^{v}v)\in R^{p_v}$$

其中，可学习的参数包括$W_i^q\in R^{p_q\times d_q}$、$W_i^k\in R^{p_k\times d_k}$和$W_i^v\in R^{p_v\times d_v}$以及代表注意力汇聚的函数$f$。 $f$可以是《深入理解深度学习——注意力机制（Attention Mechanism）：注意力评分函数（Attention Scoring Function）》中的加性注意力和缩放点积注意力。 多头注意力的输出需要经过另一个线性转换， 它对应着$h$个头连结后的结果，因此其可学习参数是$W_i^o\in R^{p_p\times h_{p_v}}$：
$$W^o\begin{array}{c}\left[\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_h\end{array}\right]\end{array}\in R^{p_o}$$

基于这种设计，每个头都可能会关注输入的不同部分， 可以表示比简单加权平均值更复杂的函数。

自注意力的实例

多头注意力是指我们可以使用多个注意力头，而不是只用一个。我们可以应用在《深入理解深度学习——注意力机制（Attention Mechanism）：自注意力（Self-attention）》中的计算注意力矩阵$Z$的方法，来求得多个注意力矩阵。让我们通过一个例子来理解多头注意力层的作用。以“All is well.”这句话为例，假设我们需要计算“well”的自注意力值：
$$Z_{\text{well}}=0.6\times V_{\text{all}}+0.0\times V_{\text{is}}+0.4\times V_{\text{well}}$$

“well”的自注意力值是分数加权的值向量之和，并且它实际上是由“All”主导的。也就是说，将“All”的值向量乘以0.6，而“well”的值向量只乘以了0.4。这意味着$Z_{\text{well}}$将包含60%的“All”的值向量，而“well”的值向量只有40%。这只有在词义含糊不清的情况下才有用。还是以《深入理解深度学习——注意力机制（Attention Mechanism）：自注意力（Self-attention）》中的例句为例：

A dog ate the food because it was hungry.
一只狗吃了食物，因为它很饿。

现在我们假设$Z_{\text{it}}=0.00\times V_{\text{A}}+1.00\times V_{\text{dog}}+0.00\times V_{\text{ate}}+0.00\times V_{\text{the}}+0.00\times V_{\text{food}}+\cdots +0.00\times V_{\text{hungry}}$。“it”的自注意力值正是“dog”的值向量。在这里，单词“it”的自注意力值被“dog”所控制。这是正确的，因为“it”的含义模糊，它指的既可能是“dog”，也可能是“food”。如果某个词实际上由其他词的值向量控制，而这个词的含义又是模糊的，那么这种控制关系是有用的；否则，这种控制关系反而会造成误解。为了确保结果准确，我们不能依赖单一的注意力矩阵，而应该计算多个注意力矩阵，并将其结果串联起来。使用多头注意力的逻辑是这样的：使用多个注意力矩阵，而非单一的注意力矩阵，可以提高注意力矩阵的准确性。

假设要计算两个注意力矩阵$Z_1$和$Z_2$。首先，计算注意力矩阵$Z_1$。我们已经知道，为了计算注意力矩阵，需要创建三个新的矩阵，分别为查询矩阵、键矩阵和值矩阵。为了创建查询矩阵$Q_1$、键矩阵$K_1$和值矩阵$V_1$，我们引入三个新的权重矩阵，称为$W_1^q$、$W_1^k$和$W_1^v$。用矩阵$X$分别乘以矩阵$W_1^q$、$W_1^k$和$W_1^v$，就可以依次创建出查询矩阵、键矩阵和值矩阵。

基于以上内容，注意力矩阵$Z_1$可按以下公式计算得出：
$$Z_1=\text{Softmax}(\frac{Q_1{K}_1^T}{\sqrt{d_k}})V_1$$

接下来计算第二个注意力矩阵$Z_2$。为了计算注意力矩阵$Z_2$，我们创建了另一组矩阵：查询矩阵$Q_2$、键矩阵$K_2$和值矩阵$V_2$，并引入了三个新的权重矩阵，即$W_2^q$、$W_2^k$和$W_2^v$。用矩阵$X$分别乘以矩阵$W_2^q$、$W_2^k$和$W_2^v$，就可以依次得出对应的查询矩阵、键矩阵和值矩阵。注意力矩阵$Z_2$可按以下公式计算得出：
$$Z_2=\text{Softmax}(\frac{Q_2{K}_2^T}{\sqrt{d_k}})V_2$$

同理，可以计算出$h$个注意力矩阵。假设我们有8个注意力矩阵，即$Z_1$到$Z_8$，那么可以直接将所有的注意力头（注意力矩阵）串联起来，并将结果乘以一个新的权重矩阵$W_0$，从而得出最终的注意力矩阵：
$$\text{Multi-head Attention}=\text{Concatenate}(Z_1,Z_2,\cdots ,Z_8)W_0$$

参考文献：
[1] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015
[2] Aston Zhang, Zack C. Lipton, Mu Li, Alex J. Smola. Dive Into Deep Learning[J]. arXiv preprint arXiv:2106.11342, 2021.