【LeetCode热题100】打卡第20天：合并区间&不同路径

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

博客主页💖：知识汲取者的博客

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

合并区间

🔒题目

原题链接：56.合并区间

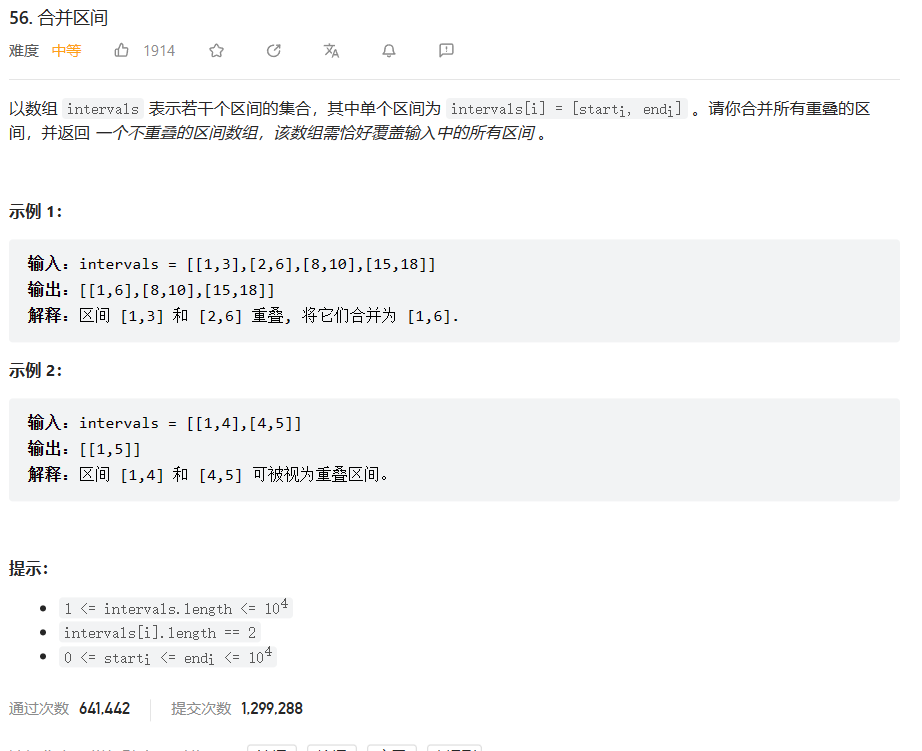
🔑题解

• 解法一：排序+枚举

  说实话，这里我一开始是没考虑到，示例数据居然是无序的，刚开始做的时候，我直接默认认为示例数据是有序的，导致接连错误。后来发现原来示例数据是无序的。所以我们一开始要对数组进行排序，这里使用了Arrays+比较器对数组进行排序。排完序后，题目就会变得很简单了，相信看完代码你应该是能够懂的，这里没有什么算法，有的就是逻辑，不懂的欢迎评论区留言(●’◡’●)

  import java.util.ArrayList;
  import java.util.Arrays;
  import java.util.List;
  
  /**
   * @author ghp
   * @title 跳跃游戏
   */
  class Solution {
      public int[][] merge(int[][] intervals) {
          if (intervals.length == 0) {
              return new int[0][2];
          }
          // 按照数组每行第一个元素进行升序排序
  //        Arrays.sort(intervals, Comparator.comparingInt(arr -> arr[0])); // 写法一
          Arrays.sort(intervals, (arr1, arr2) -> arr1[0]-arr2[0]); // 写法二
  //                Arrays.sort(intervals, new Comparator<int[]>() { // 写法二的完整写法
  //            public int compare(int[] interval1, int[] interval2) {
  //                return interval1[0] - interval2[0];
  //            }
  //        });
          List<int[]> list = new ArrayList<>();
          // 遍历数组，对数组进行合并
          for (int i = 0; i < intervals.length; i++) {
              int l = intervals[i][0];
              int r = intervals[i][1];
              if (list.size() == 0 || list.get(list.size() - 1)[1] < l) {
                  // 相邻数组没有重叠区间，不能合并
                  list.add(new int[]{l, r});
              } else {
                  // 相邻数组有重叠区间，需要合并
                  list.get(list.size()-1)[1] = Math.max(list.get(list.size()-1)[1], r);
              }
          }
          // 将list数组转化成数组，并返回
          return list.toArray(new int[list.size()][]);
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(nlogn)$
  • 空间复杂度：$O(logn)$

  其中 $n$ 为数组中元素的个数

不同路径

🔒题目

原题链接：62.不同路径

🔑题解

• 解法一：DFS（时间超限）

  直接暴力DFS，不出所料超时了

  /**
   * @author ghp
   * @title 不同路径
   */
  class Solution {
  
      private int count = 0;
  
      public int uniquePaths(int m, int n) {
          bfs(m, n, 0, 0);
          return count;
      }
  
      private void bfs(int m, int n, int r, int d) {
          if (r == n - 1 && d == m - 1) {
              // 当前路径到达终点
              count++;
              return;
          }
          if (r > n - 1 || d > m - 1) {
              // 出界
              return;
          }
          // 往左走
          bfs(m, n, r + 1, d);
          // 往下走
          bfs(m, n, r, d + 1);
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(2^n)$
  • 空间复杂度：$O(n\ast m)$

  其中 $n$ 为列，$m$为行

  代码优化：DFS+记忆搜索

  前面我们直接暴力DFS，发现时间复杂度居然高达$2^n$，显然很容易超时。这里我们可以使用一个数组来记录每次遍历能够到达终点的路径条数（俗称“记忆搜索”），这样能够避免很多重复的搜索，从而大大提高搜索效率

  import java.util.Arrays;
  
  /**
   * @author ghp
   * @title 不同路径
   */
  class Solution {
  
      public int uniquePaths(int m, int n) {
          int[][] path = new int[m][n]; // 用于记录每个节点到达终点的次数
          // 初始化path数组
          for (int i = 0; i < path.length; i++) {
              Arrays.fill(path[i], -1);
          }
          path[m-1][n-1] = 1;
          // 深搜
          dfs(path, m, n, 0, 0);
          return path[0][0];
      }
  
      private int dfs(int[][] path, int m, int n, int y, int x) {
          if (path[y][x] != -1) {
              // 该点已经走过，直接返回
              return path[y][x];
          }
          int count = 0;
          if (y + 1 < m) {
              // 往下
              count += dfs(path, m, n, y + 1, x);
          }
          if (x + 1 < n) {
              // 往右
              count += dfs(path, m, n, y, x + 1);
          }
          // 记录当前节点能够到达终点的路径条数（核心步骤）
          path[y][x] = count;
          return count;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n\ast m)$
  • 空间复杂度：$O(n\ast m)$

  其中 $n$ 为列，$m$为行

• 解法二：动态规划

  这题使用动态规划来写是最简单的😄！每一个节点都有两个状态，要么是从上节点过来的，要么是从左节点过来的，所以我们可以很容易就得到一个状态转移方程$f(i,j)=f(i,j-1)+f(i-1,j)$，也就是说只要上节点或者左节点能够到达终点，那么当前节点一定能够到达终点（实在不懂的可以画个草图一下就能理解了，这题堪称动态规划入门题了，对新手是分友好🤭）

  

  /**
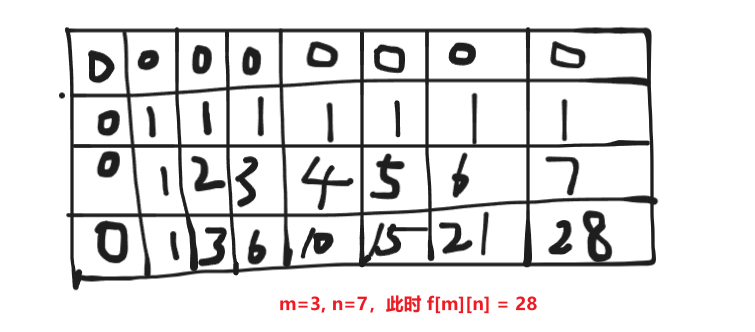
   * @author ghp
   * @title 不同路径
   */
  class Solution {
  
      public int uniquePaths(int m, int n) {
          int[][] f = new int[m+1][n+1];
          f[1][1] = 1;
          for (int i = 1; i <= m; i++) {
              for (int j = 1; j <= n; j++) {
                  // 这里要用自加，是为了防止f[1][1]为0
                  f[i][j] += f[i - 1][j] + f[i][j - 1];
              }
          }
          return f[m][n];
      }
  }
  

• 解法三：组合数学

  LeetCode官方提供的代码题解，简洁而优雅。感兴趣的可以去官网查看题解详情分析

  class Solution {
      public int uniquePaths(int m, int n) {
          long ans = 1;
          for (int x = n, y = 1; y < m; ++x, ++y) {
              ans = ans * x / y;
          }
          return (int) ans;
      }
  }
  
  作者：LeetCode-Solution
  链接：https://leetcode.cn/problems/unique-paths/solution/bu-tong-lu-jing-by-leetcode-solution-hzjf/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。