一.树之习题选讲-Tree Traversals Again
树习题-TTA.1 题意理解
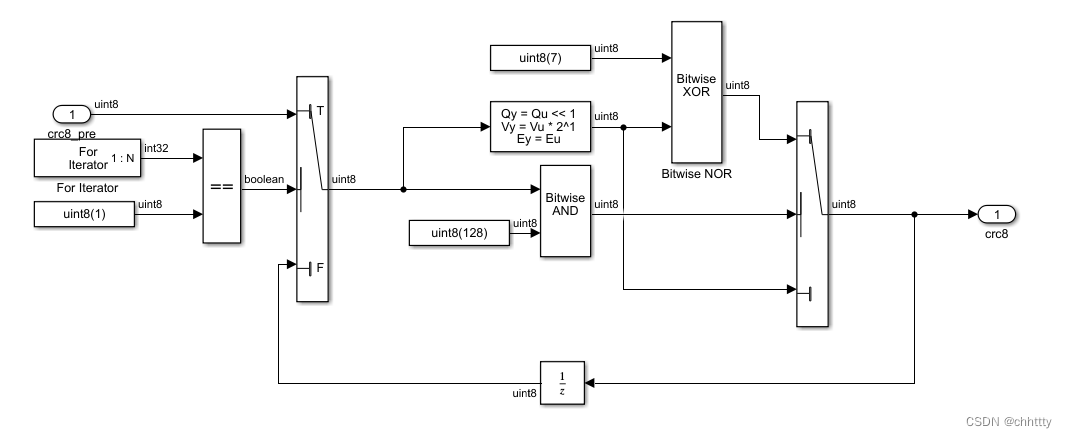
非递归中序遍历的过程
- 1. Push的顺序为先序遍历(pre)
- 2. Pop的顺序给出中序遍历(in)

树习题-TTA.2 核心算法

上图分别是先序、中序、后序遍历通过规律我们可以看到他们之间的位置分配
//伪代码
void solve(int preL,int inL,int n)
{
if(n == 0) return;//n等于0的时候什么都不做(n真的会右等于0的时候吗?为什么写他?)调用完了
之后右边没有元素,此时n等于0,进行判断正常结束进程
if(n == 1){post[postL] == pre[preL];return;}//只有一个结点的时候,pre、in、post都
应该等于同一个数字
root = pre[preL];
post[postL+n-1] = root;
for(i = 0; i < n; i++)
if(in[inL+i] == root) break; //判断in这个位置上的元素是不是等于根结点。结合上图看
就是要找根结点在图中的哪里,找到了就跳出循环
//在跳出循环之后我们就同时知道了左子树包含了多少元素,然后递归的去解决左边跟右边的问题
L = i;R = n - L -1//得出左右两边的元素个数
solve(preL+1,inL,postL,L);//左边的
solve(preL+L+1,inL+L+1,postL+L,R)//右边的。第一个是蓝色的第一个位置,第二个也是蓝色一
个的位置,第三个是蓝色的第一个位置(和前两个不同的是这个时候1在蓝色的后面,所以不用加上1了,第四
个参数是右边子问题的总个数)
}
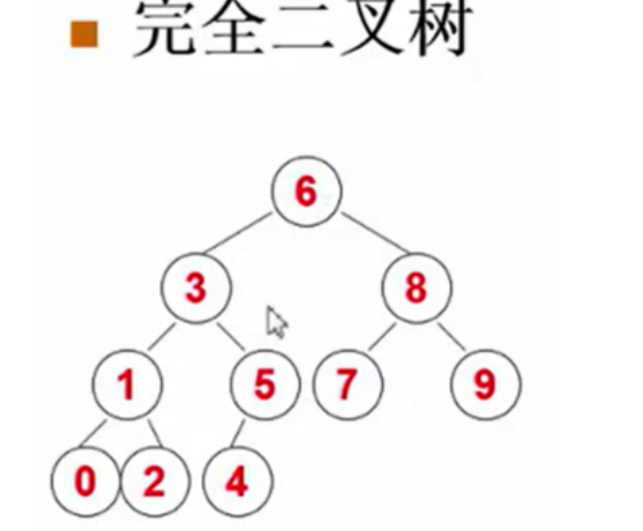
二.树之习题选讲-Complete Binary Search Tree
(完全 二叉 搜索 树)
树习题-CBST.1 数据结构的选择 题意理解

题目要求:
输入一系列整数,要填入一个完全二叉树里面,同时这颗树还需要满足二叉搜索树的性质。也就是说左边的结
点的键值都比根结点要小,右边的全部都比他要大,左右子树也都满足二叉搜索树递归的定义
经过修改后的图片如下:
树的表示法:链表 vs 数组
在这道题目中我们需要的操作:
1.填写数字(某种遍历),意思就是说对这棵树里面的每一个结点访问一次填写一个数字
2.层序遍历
为什么在很多情况下我们宁愿用链表去表示一颗树而不用数组呢?
用数组是可以的,好处是不涉及任何指针的操作。指针的操作通常是比较危险又比较耗时的
缺点:用数组去存,遇到左右不完全相等的树的时候,需要把中间那些不存在的结点的空间保留下来,要是树 极端一点就非常耗费空间,在链表就没有这个问题
在这个问题中我们需要解决的问题:
1. 完全二叉树,不浪费空间(从根结点到最后一个叶子结点一层层走下来没有一个是空的,没有一个元
素是浪费的)
2. 层序遍历 == 直接顺序输出(按照下标顺序输出就结束了,用数组的话)所以我们决定用数组解决这个
问题
树习题-CBST.2 核心算法
如果我们知道左子树一共包含了多少个结点,那就知道根结点R上放的一定是从小到大排第几位的那个
数字
如何知道左子树有多少个结点呢?
1. 给定n个数之后,完全二叉树的结构是固定的,可以非常准确的算出左边一共多少个结点
2. 先给我们要输入的序列从小到大排一个序列。根据完全二叉树一共有多少个结点,通过导出的公式
是可以精确计算他的左子树一共有多少个结点
3. 排序是典型先序遍历的应用
核心算法

TRoot是树T根结点所在的位置,那个元素的下标存在TRoot里面
void solve(int ALeft,int ARight,int TRoot)
{
//初始调用为solve(0,N-1,0)->A的起始点就是A的第0个元素,A的终止点就是A的最后一个元素(N-1
是他的下标),结果树T是完全二叉树,他的根结点一定存在T[0]这个位置,所以刚开始传入的是0
//整个函数要完成的任务就是从A传进去的这一段里面选出一个正确的数字,填到我们结果的这颗
树,TRoot的这颗树上
n = ARight - ALeft + 1;//这一段里面元素总个数n(最右边下标减去最左边下标加上1)
if(n == 0) return;
L = GetLeftLenght(n);//计算出n个结点的树(完全二叉树)其左子树有多少个结点
T[TRoot] = A[ALeft + L];
//左孩子的下标是多少?正常情况下根结点是TRoot的话那他的左孩子下标应该是TRoot×2,但是那是
在堆里面(堆的第0个元素是存放哨兵的地方,不是用来存真实值的),在本题中是从0开始算下标的
LeftRoot = TRoot * 2 + 1;//(例子:左孩子第一个元素0*2+1为1,第二个3...)
RightTRoot = LeftTRoot + 1;//(例子:右孩子第一个元素1+1为2,第二个4...)
//准备递归左右边
solve(ALeft,ALeft + L - 1,LeftTRoot);//左边,ALeft + L - 1是取掉根结点元素的前一个
值
solve(ALeft + L + 1,ARight,RightTRoot);//右边
}
排序(目前凑合用的,后面详细讲解使用)
库函数:qsort
#include<stdlib.h>//调用qsort
int main()
{
....
qsort(A,N,sizeof(int),compare);//根据返回的两个数是正数还是负数还是0来决定两个元素谁
排在前面或者后面或者不做交换
//第一个参数:待排序序列的首元素的位置(就是把读进来的数存在一个叫A的数组里面)也就是说如果我
们要将数组排序的话,这个就是数组首元素的地址
//第二个参数:代排序列的总长度(一共要排N个元素)
//第三个参数:要排元素的大小
//第四个参数:不是变量,是一个函数的名字(可以不叫compare,这个随意),他的作用是比较两个元
素的大小。因为qsort就是比较一对元素的大小来决定哪个元素应该在前面的,哪个元素应该在后面的
....
}
/*compare标准接口
int compare(const void*a,const void*b)传入的是两个带比较元素的指针。需要返回的是三种
整数之一(负数正数或者0,这里浙大的课程中字幕第一次出错负数显示为复数,但其实是负数,需要注意)
{
return *(int*)a - *(int*)b;//后序也可以非常复杂
}
*/
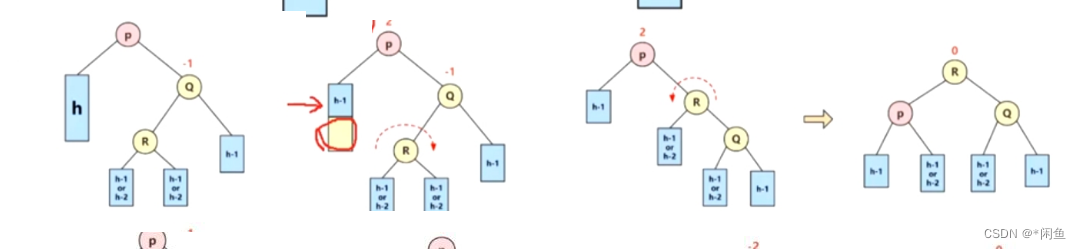
树习题-CBST.3 计算左子树的规模
h是层数
真正计算H的时候X的出来的可能不是整数,但不要紧,X是多少都没有关系,求H的话可以忽略掉X然后
的出来的答案向下取整即可。得到的H就是完美二叉树层数(H),然后就可以反算出X了
完美二叉树的左子树:
如果X的个数蔓延到右子树那边去的话(就是最后一层的x跑到右边去,那上面左子树的式子就不能加上X)
所以我们需要知道最下面一层x的最大值和最小值可以取多少
1. 在这个式子中,最小值X要取到0(为什么不是1而是0呢?L是左子树哦)
1. 因为在上述式子中H至少为2啦,H为1是根结点的位置层数,左子树至少从第二层开始,最少
只有他自己一个
2. 要使
得到正确结果, 能取的最大值是