• 研究背景

科学和工程中的许多应用需要求解具有不同方程系数、不同边界条件甚至不同求解域形状的偏微分方程(Partial Differential Equation，PDE)，即需要求解一个方程族而不是单个方程。这类应用经常在反问题求解、控制和优化、风险评估和不确定性量化领域中出现。从数学上讲，这类应用需要求解以下参数化偏微分方程(Parametric PDE)：

第一类方法是用神经网络去近似单个PDE的解。这类方法主要依赖控制方程（或其变分形式）和边界条件来训练神经网络。例如，物理信息神经网络(Physics-Informed Neural Networks，PINNs)和DGM (Deep Galerkin Method)通过约束深度神经网络的输出来满足给定的控制方程和边界条件。DRM (Deep Ritz Method)利用偏微分方程的变分形式求解可以表示为等效能量最小化问题的偏微分方程。基于偏微分方程的弱形式，弱对抗网络(Weak Adversarial Network，WAN)将弱解和测试函数分别参数化为Primal神经网络和Adversarial神经网络。这些方法都可以在无监督的方式下工作，即不需要利用传统的数值方法来生成标签数据。然而，当采用这类的方法求解参数化偏微分方程时，我们需要针对每一个PDE参数去单独训练一个模型。当需要求解具有大量PDE参数的参数化偏微分方程时，这类方法的计算量大且不切实际。DRM提出采用迁移学习的方法降低从头训练模型的成本，即将某个任务下训练得到的神经网络权重作为另一个任务的初始化权重。然而当两个任务的相关性较小时，迁移学习的方法相较于从头训练神经网络并没有带来明显的好处。

第二类方法使用神经网络来学习两个无限维函数空间之间的解映射（即PDE参数到方程解的映射）。例如，PDE-Net 用受矩约束的卷积层来逼近空间微分算子（类似于传统的有限差分方法），它能够从观察到的动力学数据中发现支配该动力学系统的控制方程，同时进行快速而准确的预测。深度算子网络(Deep Operator Network，DeepONet)使用两个子网分别对PDE参数和坐标进行编码，并将两个子网的输出做内积以得到方程的解。傅立叶神经算子 (Fourior Neural Operator，FNO)直接在傅立叶空间参数化积分核，从而实现表征能力更强的网络架构。这类方法的显著优点是一旦训练好了神经网络，预测时间几乎可以忽略不计。尽管这类方法在很多应用中都展示出了很理想的效果，但依然存在如下几个问题：1)复杂的物理、生物或工程系统中，标签数据获取成本过高，然而当可用的标签数据很少时，这些模型的泛化能力会很差；2) 这类方法中的大多数都需要一个预定义的网格，并利用网格上的标签数据进行训练和推理；3) 泛化性能难以保证，特别是将模型用于外插时（即用于训练和推理的PDE参数来自于不同的概率分布）；4) 这些方法会直接将PDE参数作为神经网络的输入，如果是异构的，这将给网络架构的设计带来不便。虽然PI-DeepONet (Physics-Informed DeepONet)可以在无标签数据和无需重新训练的情况下学习PDE参数到方程解的映射并且不需要一个预定义的网格，但是它需要在参数空间中收集大量的训练样本才能获得一个相对可接受的精度，并且其不能灵活地处理异构PDE参数。

传统意义上的机器学习针对的是一个学习任务，而元学习(Meta Learning)基于一系列相关的学习任务来改进学习算法本身，以使得模型可以更快、更好地处理新的学习任务。经典的元学习算法：MAML和Reptile，已在很多领域被广泛使用。这些元学习算法试图找到一个泛化能力更强的初始模型，以使其能够在少量梯度更新下就能处理新的学习任务。借鉴元学习的思想可以求解参数化偏微分方程，即将不同的PDE参数对应的方程求解视作是不同的学习任务。Meta-MgNet是第一个将求解参数化偏微分方程视为元学习问题的工作，它基于超网和多重网格算法。Meta-MgNet利用任务之间的相似性自适应地生成良好的平滑算子，从而加快求解过程，但是其无法直接应用于不能使用多重网格算法的偏微分方程。最近有研究者将Reptile算法与PINNs相结合用于加速偏微分方程的求解。但是我们通过实验发现，对于一些训练难度较大的偏微分方程来说（例如参数化的带点源的麦克斯韦方程组），Reptile算法并没有明显的求解速度提升。

• 论文主要内容简介

通过将求解参数化的偏微分方程视为一个元学习问题，我们提出了元自动解码器 (Meta-Auto-Decoder , MAD)，这是一种无网格、无监督的深度学习方法，通过自动解码器(Auto-Decoder)架构将（异构）偏微分方程参数隐式编码为隐向量，使得预训练模型能够快速适配到新的方程实例。

论文的主要贡献如下：

1. 提出了一种求解参数化偏微分方程的无网格、无监督的深度神经网络方法。基于元学习的概念，一旦预先训练好神经网络，求解一个新任务只需要进行少量迭代数目的微调。此外，MAD采用的自动解码器架构可以实现对不同PDE参数的自动编码。
2. 从流形学习的角度分析了MAD方法的有效性。简而言之，神经网络通过预训练来逼近解流形，而微调对应着在解流形或解流形所在的邻域中搜索方程解。
3. 通过大量的数值实验验证了MAD方法的有效性，结果表明MAD算法能够显著提高模型的收敛速度，并且具有良好的外插能力。

• 代码链接

论文: Meta-Auto-Decoder for Solving Parametric Partial Differential Equations

https://arxiv.org/abs/2111.08823

代码链接:

https://gitee.com/mindspore/mindscience/tree/master/MindElec/examples/physics_driven/incremental_learning

• 算法框架与技术要点

技术要点1：MAD的预训练和微调

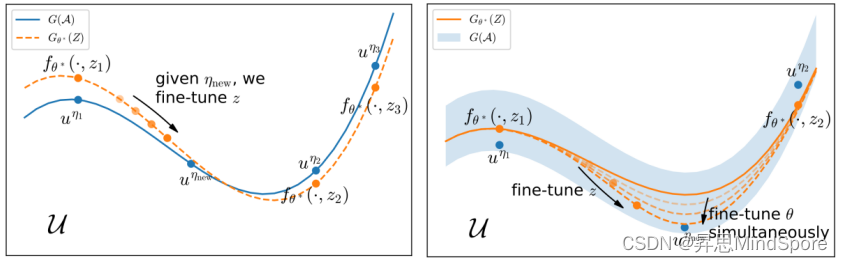
图四：从流形学习角度解释MAD方法的有效性。

• 实验

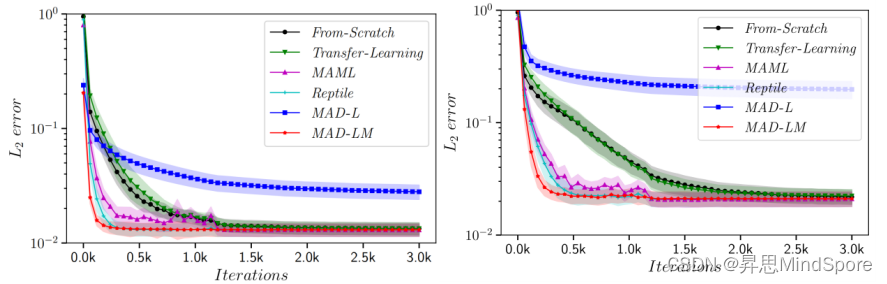
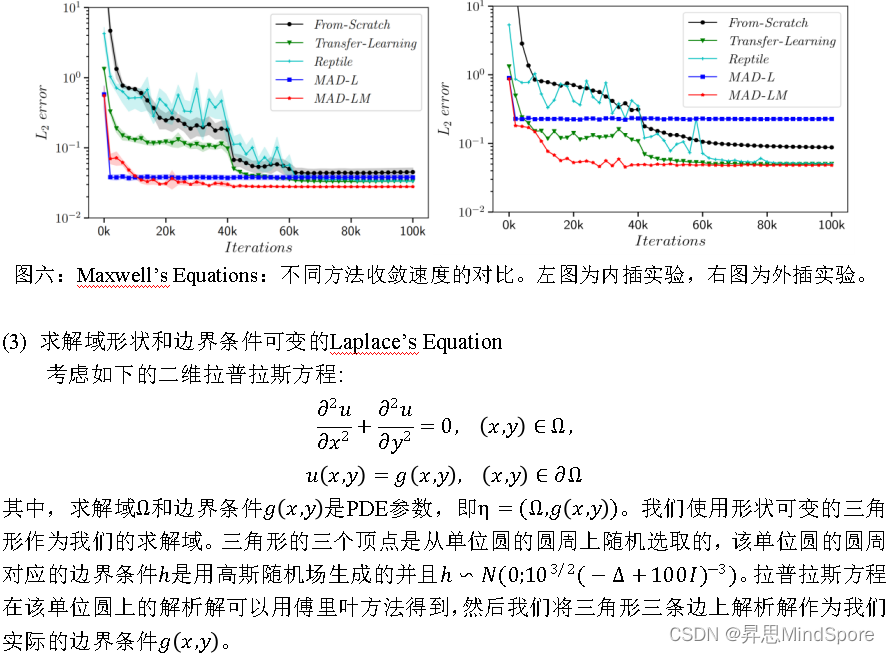
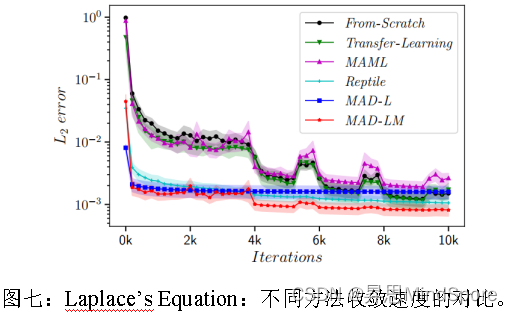
• 总结

基于元学习思想，本文提出了一种求解参数化偏微分方程的无网格、无监督的深度学习方法MAD。MAD的预训练是从一组采样任务中学习有用的信息，模型通过加载预训练得到的网络权重可以加快其在微调时的收敛速度。不仅如此，MAD还可以将异构的PDE参数隐式编码为可训练的隐向量。我们还从流形学习的角度分析了MAD方法的有效性，并通过大量的数值实验验证了MAD方法的有效性。