前言:
通过对【蓝桥杯】2020初赛的一道求既约分数的题目的讲解,引出关于求“最大公约数与最小公倍数”的方法汇总。
对于“最大公约数与最小公倍数”来说,求解都有一些固定的方法,而这些方法一般都是固定的,只需要掌握方法,在日后遇到类似题目直接套用即可。
目录
蓝桥杯题目:既约分数
思路分析:
完整代码:
求最大公约数:
一、辗转相除法
二、更相减损法
三、穷举法
四、递归(辗转相除)
求最小公倍数:
一、穷举法
二、a*b/最大公约数
蓝桥杯题目:既约分数
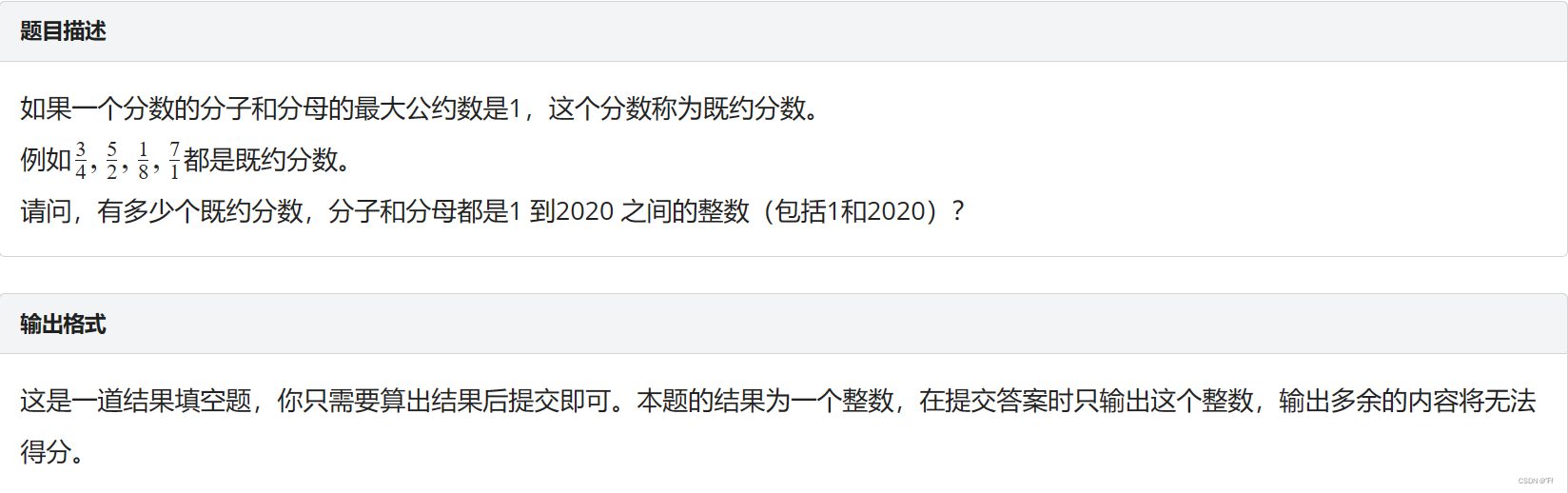
思路分析:
首先我们需要利用双层循环搭配产生分子与分母,得到这些数字后,在循环中判断这两个数是否满足他们的最大公约数为1即可,那么我们先做框架,再做细节,所以主函数(框架)这样设计:
int main()
{
int i = 0;
int count = 0;
for (i = 1; i <= 2020; i++)
{
int j = 0;
for (j = 1; j <= 2020; j++)
{
if (gcd(i, j) == 1)//判断他们的最大公约数是否为1
count++;
}
}
printf("%d", count);
return 0;
}之后我们只需要再做细节,设计函数,如果你不知道如何设计求最大公约数的函数的话,在文章后面详细讲解了如何求最大公约数以及如何求最小公倍数。
完整代码:
int gcd(int a, int b)
{
int z = b;
while (a % b)
{
z = a % b;
a = b;
b = z;
}
return z;
}
int main()
{
int i = 0;
int count = 0;
for (i = 1; i <= 2020; i++)
{
int j = 0;
for (j = 1; j <= 2020; j++)
{
if (gcd(i, j) == 1)
count++;
}
}
printf("%d", count);
return 0;
}答案:2481215
求最大公约数:
一、辗转相除法
通俗的将就是让两个数除留余数,当余数不为0时,继续用除数除以得到的余数,重复这一过程直到余数为0,此时的除数即为最大公约数,用图片表示为:
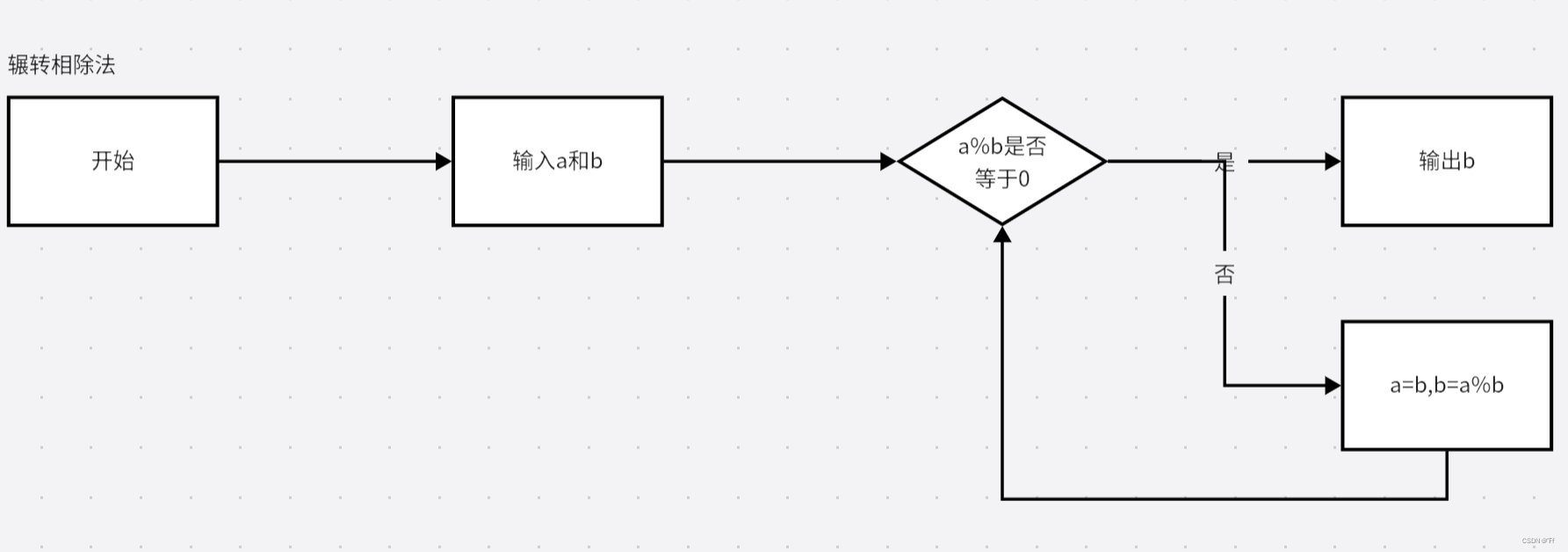
代码实现:
int gcd(int a, int b)
{
int z = b;//如果初始情况a%b的结果为0,那么此时除数b的值即为最大公约数
while(a % b!= 0)
{
z = a % b;
a = b;
b = z;
}
return z;
}二、更相减损法
以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。循环这个操作,直到所得的减数和差相等为止。
代码实现:
int gcd(int a,int b)
{
while (a != b)
{
if (a > b)
{
a = a - b;
}
else
{
b = b - a;
}
return a;
}
}三、穷举法
穷举法的思路很简单,他的最坏情况时间复杂度极高,不建议使用。
利用定义暴力穷举,创建一个临时变量保存其中一个数的值,循环判断是否满足最大公约数的定义,不满足就减一,直到找到这个数。
代码实现:
int gcd(int a, int b)
{
int tmp = 0;
for (tmp = a; ; tmp--)
{
if ((0 == a % tmp) && (0 == b % tmp))
break;
}
return tmp;
}四、递归(辗转相除)
思想同辗转相除法。
int gcd(int a, int b)
{
if (b == 0)
return a;
else
return gcd(b, a % b);
}求最小公倍数:
一、穷举法
与求最大公约数的穷举法一样的思路,同样他最坏情况的时间复杂度非常高,不建议使用。
代码实现:
int lcm(int a, int b)
{
int tmp = a > b ? a : b;
while (1)
{
if ((0 == tmp % a) && (0 == tmp % b))
break;
tmp++;
}
return tmp;
}我们可以对这个穷举法进行一定的优化,由每次加一试数改为以乘数加一试数。
代码实现:
int lcm(int a, int b)
{
int i = 1;
while ((a * i) % b)
{
i++;
}
return (a * i);
}二、a*b/最大公约数
此方法利用最小公倍数的定义得到,即最小公倍数= a*b/最大公约数。
int lcm(int a, int b)
{
int z = 0;
int n = a * b;
//计算最大公约数z
while (z = a % b)
{
a = b;
b = z;
}
return (n / z);//最小公倍数=(a*b)/最大公约数
}求最大公约数类似的问题在算法比赛中很常见,希望这篇文章可以给你带来收获。
🔥🔥🔥