来源：力扣（LeetCode）

描述：

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

实现 TreeAncestor 类：

• TreeAncestor（int n， int[] parent） 对树和父数组中的节点数初始化对象。
• getKthAncestor(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

示例 1：

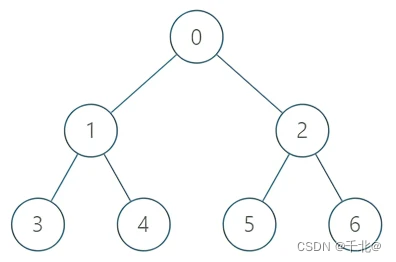
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

输出：
[null,1,0,-1]

解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

提示：

• 1 <= k <= n <= 5 * 10⁴
• parent[0] == -1 表示编号为 0 的节点是根节点。
• 对于所有的 0 < i < n ，0 <= parent[i] < n 总成立
• 0 <= node < n
• 至多查询 5 * 10⁴ 次

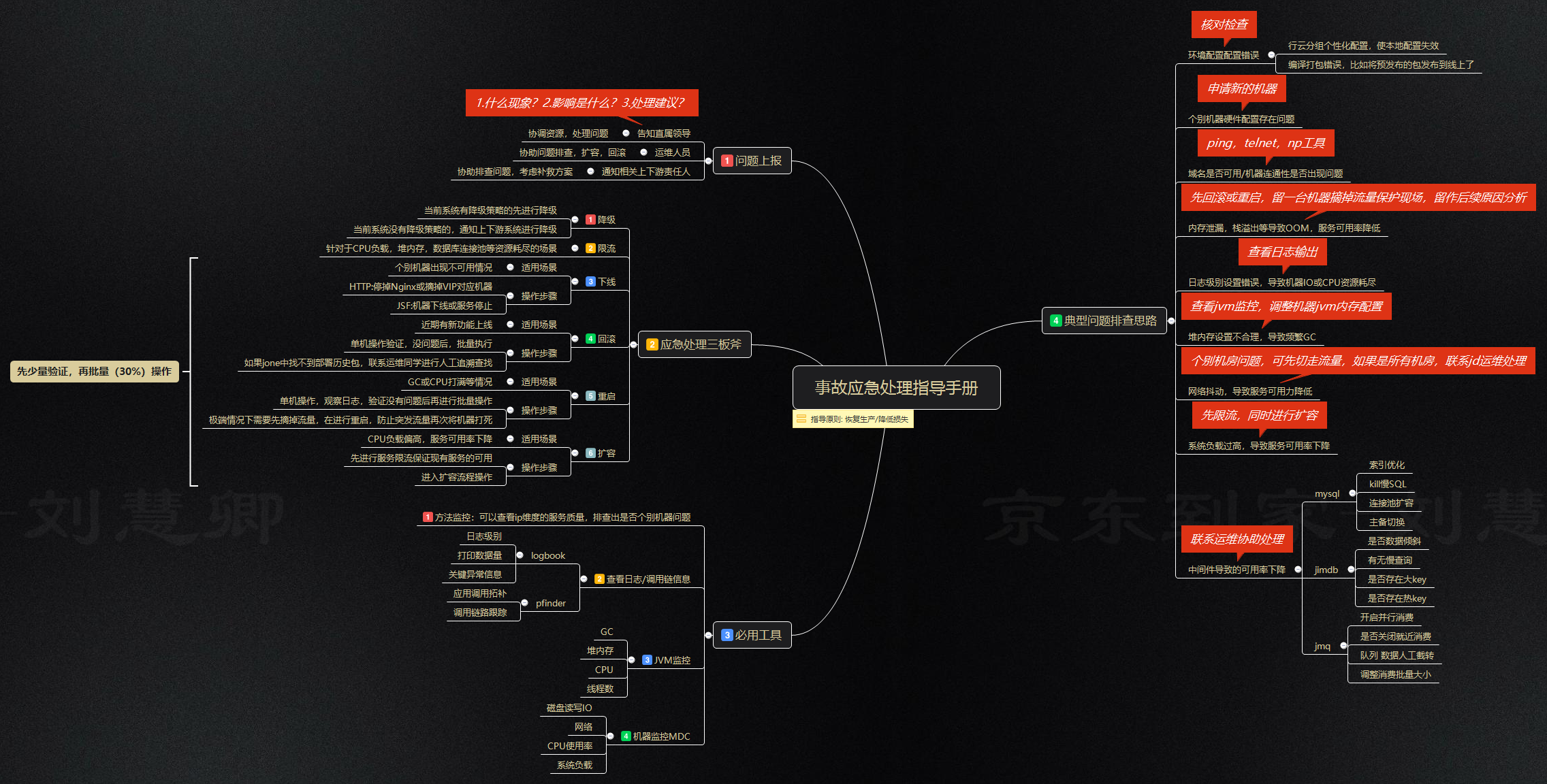
方法：倍增

思路

倍增的思路类似于动态规划，定义 ancestors[i][j] 表示节点 i 的第 2^j 个祖先。此题中，树最多有 50000 个节点，因此 ancestors 的第二维度的最大值可以设为 16。根据定义，ancestors[i][0] = parent[i]。状态转移方程是 ancestors[i][j] = ancestors[ancestors[i][j−1]][j−1]，即当前节点的第 2^j 个祖先，是他的第 2^j−1 个祖先的第 2^j−1 个祖先。当第 2^j 个祖先不存在时，记为 −1。

查询时，需要将 k 的二进制表示从最低位到最高位依次进行判断，如果第 j 位为 1，则节点 node 需要进行转移到 ancestors[node][j]，表示 node 向祖先方向移动了 2^j 次。直至遍历完 k 所有位或者 node 变为 −1。

代码：

class TreeAncestor {
public:
    constexpr static int Log = 16;
    vector<vector<int>> ancestors;

    TreeAncestor(int n, vector<int>& parent) {
        ancestors = vector<vector<int>>(n, vector<int>(Log, -1));
        for (int i = 0; i < n; i++) {
            ancestors[i][0] = parent[i];
        }
        for (int j = 1; j < Log; j++) {
            for (int i = 0; i < n; i++) {
                if (ancestors[i][j - 1] != -1) {
                    ancestors[i][j] = ancestors[ancestors[i][j - 1]][j - 1];
                }
            }
        }            
    }

    int getKthAncestor(int node, int k) {
        for (int j = 0; j < Log; j++) {
            if ((k >> j) & 1) {
                node = ancestors[node][j];
                if (node == -1) {
                    return -1;
                }
            }
        }
        return node;
    }
};

执行用时：304 ms, 在所有 C++ 提交中击败了68.35%的用户
内存消耗：113 MB, 在所有 C++ 提交中击败了77.85%的用户
复杂度分析
时间复杂度：初始化的时间复杂度是 O(n×logn)，单次查询的时间复杂度是 O(logn)。
空间复杂度：初始化的空间复杂度是 O(n×logn)，单次查询的空间复杂度是 O(1)。
author：LeetCode-Solution