本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
文章目录
- 基本线性分组码与性能参数
- 线性分组码(n,k)定义
- 信道编码性能参数
- 基本线性分组码
- a.奇偶监督码
- b.恒比码
- c.汉明码
- 差错控制类型对信道编码的要求
- 1.ARQ(检错重发 自动请求重发)
- 2.FEC(前向纠错)
- 3.HEC (混合纠错 ARQ+FEC)
- 信道编码主要涉及的数学知识:有限域运算、矩阵运算
基本线性分组码与性能参数
线性分组码(n,k)定义
线性分组码是由 (n, k) 形式表示。编码器将一个 k 比特信息分组(信息矢量)转变成一个更长的由给定符号集组成的 n 比特编码分组(编码矢量)。当这个符号集包含 2 个元素 (0 and 1) 时 , 称为二进制编码。
k-bit 信息形成 2 k 2^k 2k 不同的信息序列 , 称为 k 元组。 n-bit 可以形成 2 n 2^n 2n 个不同序列,称为 n 元组。
(n,k)分组码输出的长度为n的序列称为码字。所有这些码字的集合称为该线性分组码的码组。
因为n>k,故编码时需按某种规则加入r=n-k个监督(校验)码元。
对于分组码(n,k),定义
- 编码效率: k/n
- 编码冗余度:(n-k)/n
线性分组码的几个重要概念
-
码距(汉明距离):两个码组中对应位置上具有不同二进制码元的位数
-
码重(汉明重量):线性分组码中,将码字(组)中所含 1 的数目定义为码字(组)的重量
码字0011010和1101011之间的码距为4,码字0011010的码重是3
-
编码信道:研究信道编码和译码的信道模型
- 二元码、硬判决时,建模为 BSC (二元对称)信道
- 软判决时,建模为 AWGN 信道
- 软判决与硬判决译码(简单理解:译码器输入比特的选取)
信道编码性能参数
主要的性能参数有 差错概率、编码增益、检纠错能力、编码效率k/n。
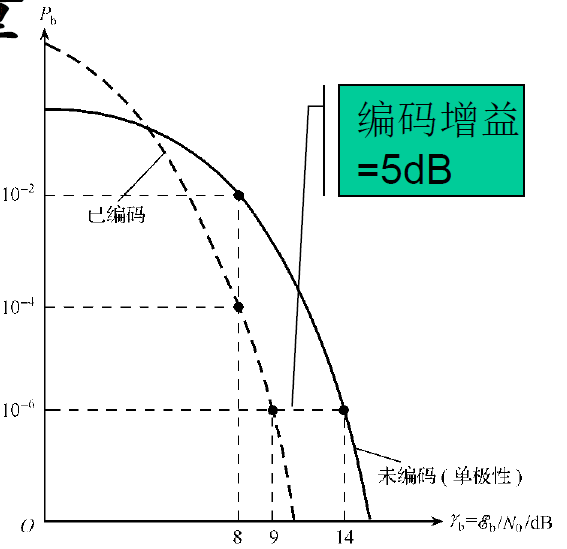
编码增益 :给定差错概率下,通过编码所能实现的比特信噪比$ 𝑬_𝒃/𝑵_𝟎$的减少量。
- 检错能力 l: d min ≥ l + 1 d_{\text {min }} \geq l+1 dmin ≥l+1
- 纠错能力 t: d min ≥ 2 t + 1 d_{\min } \geq 2 t+1 dmin≥2t+1
- 检错 l 纠错 t: d min ≥ l + t + 1 d_{\text {min }} \geq l+t+1 dmin ≥l+t+1
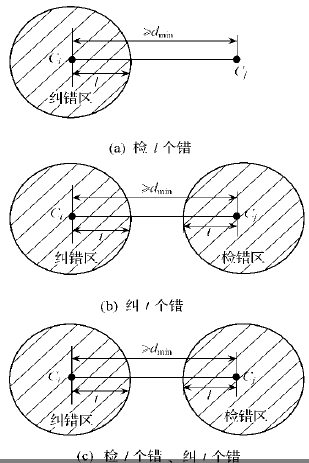
设某二元信道编码码字集合A中任意两个码字之间的汉明距离分别为:6、7和8。请问该信道编码最多能纠正几位错误,检测出几位错误。
检错能力 l: d min ≥ l + 1 d_{\text {min }} \geq l+1 dmin ≥l+1 ----> l = d - 1 = 5 最多检测5位错误
纠错能力 t: d min ≥ 2 t + 1 d_{\min } \geq 2 t+1 dmin≥2t+1 ----> t = (d - 1) / 2 = 2.5 取整,最多纠2位错
基本线性分组码
a.奇偶监督码
码字由 n 个码元组成, n - 1个信息码元,另一码元为奇(偶)监督码元 **(n, n-1)**奇偶监督码.
码率: (n-1)/ n
KaTeX parse error: Unknown column alignment: C at position 16: \begin{array} C̲C = (C_{n-1}, C…
上式=0 (偶校验)or 1(奇校验)
可检测到奇数个错误图样, 如果错误个数为偶数则无法检测。
考虑(4,3)偶监督码

误码率: P e = C 4 2 p 2 ( 1 − p ) 2 + C 4 4 p = 6 p 2 ( 1 − p ) 2 + p 4 P_{e}=C_{4}^{2} p^{2}(1-p)^{2}+C_{4}^{4} p=6 p^{2}(1-p)^{2}+p^{4} Pe=C42p2(1−p)2+C44p=6p2(1−p)2+p4
若 p=0.001 , 则 P e = 6 × 1 0 − 6 P_{e}=6 \times 10^{-6} Pe=6×10−6
b.恒比码
- 每个码组中 1 和 0 的个数保持恒定,因而比值恒定。我国电传通信中 5 中取 3 码 每个 5bit 码组中必须含有 3 个 1和2 个 0,总数共有 C 5 3 = C 5 2 = 10 C_{5}^{3}=C_{5}^{2}=10 C53=C52=10种来表示十进制数。
c.汉明码
- 能纠正单个随机错误的线性分组码
差错控制类型对信道编码的要求
1.ARQ(检错重发 自动请求重发)
- 适用于非实时数据传输系统
- 要求信道编码具有检错功能
利用奇偶校验比特来检错重发。接收端不纠正错误,只是简单的要求发射机重发数据。此时,发射端与接收端间的对话需要双向链路反馈信道 。
自动重发请求 (ARQ): 三种类型
- 停止——等待 ARQ (半双工)
- 具有回拉功能的连续 ARQ (全双工)
- 具有选择性重发功能的连续 ARQ (全双工)
ARQ的主要优点是,错误检测设备要比纠错设备简单得多,只需要少量的冗余。
ARQ只适用于发生错误时需要重发的情况。
2.FEC(前向纠错)
- 适用于实时通信系统中
- 要求信道编码具有纠错功能
- 比ARQ 优越的方面
- 没有可用的反向信道或 ARQ 延迟过长。
- 重发策略无法简单的实现。
- 没有纠正的错误数目需要过多的重传。
3.HEC (混合纠错 ARQ+FEC)
即能检错又能纠错
首先收端进行检错,如错误在纠错范围内则纠正,否则请求重传。
信道编码主要涉及的数学知识:有限域运算、矩阵运算
-
有限域初步知识: Galois 域——迦罗华域
-
有限域:指有限个元素的集合,可按规则进行代数四则运算,且运算结果仍属于集合中的有限元素。
-
对于二元域,记为 GF(2),其内码元满足模二运算。
-
二元扩展域 GF( 2 n 2^n 2n)——由 GF(2) 元素的一切长度为n的序列组成的集合(二进制数组的集合)。
-
设 $ \mathbf{x}, \mathbf{x}^{\prime} \in G F\left(2^{n}\right), \alpha \in G F(2)$ , 即 α \alpha α取0或1。
加法: x + x ′ = ( x n − 1 ⊕ x n − 1 ′ , x n − 2 ⊕ x n − 2 ′ , … , x 1 ⊕ x 1 ′ , x 0 ⊕ x 0 ′ ) \mathbf{x}+\mathbf{x}^{\prime}=\left(x_{n-1} \oplus x_{n-1}^{\prime}, x_{n-2} \oplus x_{n-2}^{\prime}, \ldots, x_{1} \oplus x_{1}^{\prime}, x_{0} \oplus x_{0}^{\prime}\right) x+x′=(xn−1⊕xn−1′,xn−2⊕xn−2′,…,x1⊕x1′,x0⊕x0′)
乘法: $\alpha \cdot x=\left(\alpha x_{n-1}, \alpha x_{n-2}, \ldots, \alpha x_{1}, \alpha x_{0}\right) $
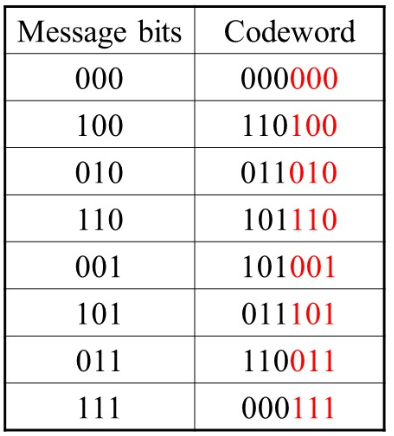
分析图的信道编码,该码的最小汉明距是3,该码能检测出2位错,能纠正1位错。该码适合纠随机错还是突发错?随机错
解:和上面类似,注意这里看的应该是Codeword。最小汉明距是3,检测出3 - 1 = 2位错,纠正(3 - 1) / 2 = 1位错,因此适合纠随机错。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.