1.问题引入

2.知识讲解

3.例题解析

【例题1】迷宫的第一条出路。

题目描述

输入格式

输出格式

样例

输入数据#1

输出数据#1

输入数据#2

输出数据#2

【例题2】迷宫的所有路径。

【例题3】走出迷宫的最少步数。

1.问题引入

拓拓小时候玩迷宫游戏时，看到迷宫图都晕头转向，但是聪明的大佬却能每次飞快地找到一条迷宫路径，从而走出迷宫。

拓拓问大佬道：“大佬，你是怎么这么快找到迷宫的路径的？”

大佬道：“写个搜索代码，一下就找到了呀！”

拓拓立马急不可待，道：“大佬快教教我，我也要学！”

同学们，你能帮助拓拓找到右边迷宫的正确路径吗？

2.知识讲解

下面总结一下基本的代码框架。全局状态变量

void dfs(当前状态) {
    if (当前状态是目标状态)          // 结束条件
        进行相应处理;
    for (所有可行的新状态) {        // 扩展新的状态
        if (新状态没有访问过 && 需要访问) {
            dfs(新状态);
        }
    }
}
int main() {
    ...
    dfs(初始状态);
    ...
}

3.例题解析

【例题1】迷宫的第一条出路。

题目描述

已知一N×N的迷宫，允许往上、下、左、右四个方向行走，现请你按照左、上、右、下顺序进行搜索，也就是 (0,−1),(−1,0),(0,1),(1,0)(0,−1),(−1,0),(0,1),(1,0)。找出第一条从左上角到右下角的路径。

输入格式

输入数据有若干行，第一行有一个自然数N（N≤20），表示迷宫的大小，其后有N行数据，每行有N个0或1（数字之间没有空格，0表示可以通过，1表示不能通过），用以描述迷宫地图。入口在左上角（1，1）处，出口在右下角（N，N）处。所有迷宫保证存在从入口到出口的可行路径。

输出格式

输出数据仅一行，为按照要求的搜索顺序找到的从入口到出口的第一条路径（搜索顺序：左、上、右、下）。

样例

输入数据#1

Copy

输出数据#1

(1,1)->(1,2)->(1,3)->(2,3)->(2,4)->(3,4)->(4,4)

Copy

输入数据#2

Copy

输出数据#2

(1,1)->(2,1)->(3,1)->(4,1)->(4,2)->(4,3)->(3,3)->(3,4)->(4,4)

【问题分析】

首先需要一个g数组存放迷宫，还需要另一个rec数组存放走过的坐标（其他的数据存储方式也可以，只要能记录点的坐标即可）。那么我们每走到一个点，就可以记录到rec数组中去。因题目要求顺序是左、上、右、下，所以在(1,1)点只能优先向右，到达(1,2)点还是向右，到达(1,3)继续向右，到达(1,4)点，发现没法可走了，如下图所示。

当在(1,4)点发现无路可走时，自动返回到上一层的(1,3)点；同样地，在(1,3)点也无路可走，返回上一层的(1,2)点；在(1,2)点也无路可走，返回上一层的(1,1)点。注意，随着点的返回，也应当让rec数组返回到上一层，若有新的方向可走，就重新记录并覆盖掉之前的错误坐标。这样就可以保证rec数组中存放的是第一条可行的路径。

现在我们回到(1,1)点，还有往下走的方向可行，继续往下搜索。和上面一样，没走到一个新的点，就记录坐标到rec数组中，直到走到终点，就得到了第一条路径。

因为要求了行走顺序是左、上、右、下，所以走到(4,3)点时是向左，不能走（左边走过了），向上可以走；到达(3,3)点时，左和上都不能走，所以往右走；到达(3,4)点，左、上、右都不能走，只能往下走，最终到达了终点(4,4)。

总结一下思路：创建rec数组，存放路径。可以继续走的时候，存放下一个点放到rec数组中。当四个方向都不能走的时候，递归回到上一层，rec数组的记录的位置上移一层。这样，就可以覆盖掉错误的路径。当我们走到终点时，就结束。

我们可以用递归函数中的参数k记录到达rec的哪一层。dfs(x,y,k)表示向路径数组rec中第k行的位置，记录一个坐标(x,y)。在递归下一层时，和之前的深搜一样，要传参新的点和新的位置dfs(nx,ny,k+1)，存放下一个点。

参考代码如下：

#include <bits/stdc++.h>
using namespace std;
int n;
char a[25][25];  //存放迷宫
int rec[410][2];  //路径数组，存放迷宫的第一条正确路径
//方向数组：左、上、右、下
int dx[4] = {0, -1, 0, 1};
int dy[4] = {-1, 0, 1, 0};
bool flag = false;  //用于标记搜索结束
void display(int k) {  //自定义函数，用于输出第一条路径
    for (int i = 1; i <= k; i++) {
        cout << "(" << rec[i][0] << "," << rec[i][1] << ")";
        if (i != k) cout << "->";
    }
}
void dfs(int x, int y, int k) {
    rec[k][0] = x, rec[k][1] = y; //向rec的第k行记录当前点的坐标(x,y)
    a[x][y] = '1'; //修改当前点为'1'，防止死循环和提高效率
    if (x == n && y == n) {
        display(k); //打印路径
        flag = true; //标记结束搜索
    }
    if(flag) return; //第一条路径找到了，就结束 if(flag) exit(0); 
    for (int i = 0; i < 4; i++) { //由点(x,y)扩展 新的点
        int nx = x + dx[i], ny = y + dy[i];
        if (a[nx][ny] == '0')  //新的点可以访问
            dfs(nx, ny, k + 1);
    }
}
int main() {
    cin >> n;//n行n列
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> a[i][j];
    dfs(1, 1, 1);//调用深搜函数
    return 0;
}

说明：

（1） rec数组至少要开辟400行，原因是因为最多会有20×20个坐标。

（2）题目没有判断超过边界，是因为存放迷宫的数组是char类型的全局数组，全部初始化为'\0'（就是ASCII码值为0的字符）。同样地，第0行、第0列、第n+1行、第n+1列也会自动初始化为字符'\0'，自然也就不等于字符'0'（ASCII码值为48）。

（3）因为（2）的原因，建议不要使用0下标开始存放迷宫，而且数组要稍微开大一些。

【例题2】迷宫的所有路径。

拓拓在森林里游玩，不小心走进了一个迷宫里面，这个迷宫是一个n行m列（n,m≤10）的矩阵，迷宫中有些格子是可以走的，有些格子是不能走的，能走的格子用“o”（小写字母o）表示，不能走的格子用“#”表示。拓拓选择走出迷宫的策略是：先向右，如果右边走不通则选择向下，如果下边走不通则选择向左，如果左边走不通则选择向上；如果四个方向都走不通，则后退选择其他能走的路径。拓拓从类似样例所示的迷宫的左上角（1,1）点进入迷宫（请注意：入口1,1和出口的n,m点都不是#），请问拓拓有哪些方法可以走出迷宫，走到（n,m）点；请编程求出所有可能的路径，输出这些路径，如果不存在任何的路径可以走出迷宫，请输出“no”。

【问题分析】

和上一题一样，我们创建a数组用来存放迷宫，创建rec数组存放路径。不同的是，这一题需要输出所有的路径，所以不能简单的把走过的路标记一下，还要考虑到后面新的路径。所以我们在调用dfs之前，把起点标记一下，然后在dfs的过程中，每次标记走过的点，当回到本层递归时，再取消标记。这样既能保证递归过程中不会往回走，还能保证所有的路径走完后，回到当前点还可以走新的路径。

#include <bits/stdc++.h>
using namespace std;
char a[15][15];  //存图
int n, m, qx, qy, zx, zy;
int dx[] = {0, 1, 0, -1};
int dy[] = {1, 0, -1, 0};
int rec[110][2];  //存放路径
int cnt;  //路径个数
void dfs(int x, int y, int k) {
    rec[k][0] = x, rec[k][1] = y;  //向rec数组中第k层存放点(x,y)
    if (x == n && y == m) {  //判断是否到达终点
        cout << ++cnt << ":";
        for (int i = 1; i < k; i++)
            cout << rec[i][0] << "," << rec[i][1] << "->";
        cout << rec[k][0] << "," << rec[k][1] << endl;
        return ;
    }
    for (int i = 0; i < 4; i++) {  //扩展新的点
        int nx = x + dx[i], ny = y + dy[i];
        if (a[nx][ny] == 'o') {  
            a[nx][ny] = '#';    //已经走过，标记为不可通行
            dfs(nx, ny, k + 1);
            a[nx][ny] = 'o';    //全部走完，取消标记
        }
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    a[1][1] = '#';//注意：起始点需要在dfs之前标记为已走过=
    dfs(1, 1, 1);
    if (cnt == 0) cout << "no";
    return 0;
}

说明：（1）题目中，可以不需要判断是否超过边界，原因和上一题的说明一样。

（2） main函数调用dfs函数之前，需要提前标记起点，否则在递归的过程中，可能再次回到起点，把起点存储两次。

（3）因为是输出所有的路径，需要dfs函数把所有可能的情况都递归搜索一遍，所以不需要提前结束dfs函数。

【例题3】走出迷宫的最少步数。

一个迷宫由R行C列格子组成，有的格子里有障碍物，不能走；有的格子是空地，可以走。给定一个迷宫，求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走，不能斜着走。空地格子用'.'表示，有障碍物的格子用'#'表示。计算步数要包括起点和终点。

输入数据：

4 
....
....
.###
....

输出数据：

【问题分析】

首先需要一个char数组存放迷宫，考虑到每次递归搜索都要记录起点到当前点的步数，我们可以再开辟一个step数组，记录从起点到任何一个点的最短距离，当所有的路径搜索完后，就可以得到起点到终点的最短距离了。

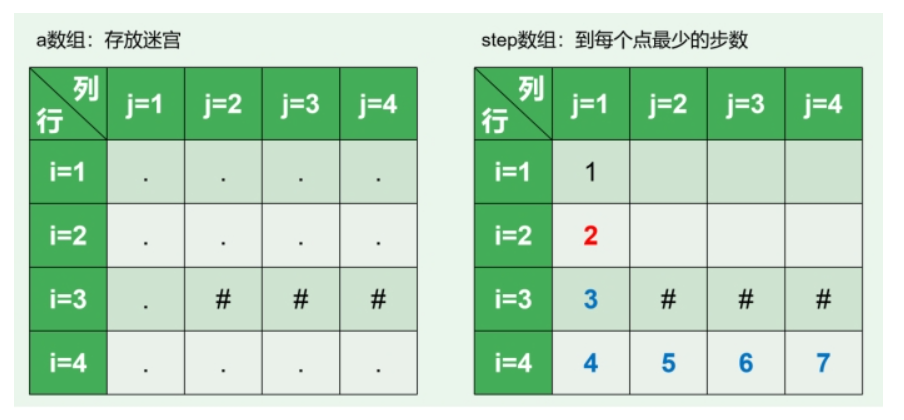
如果走到某个点(x,y)需要的步数，比step数组中记录的最少步数还少，则按照新的方案走该点。注意到step数组的每个元素的初始值可以设置为INT_MAX。最终step数组记录了从起点到每个点至少需要多少步，step[n][m]就是最终结果。

#include<bits/stdc++.h>
using namespace std;
int r, c;
char a[50][50]; //地图
int step[50][50]; //存步数
int dx[] = {0, 0, 1, -1}; //没规定方向，保证是四个正确的方向即可
int dy[] = {1, -1, 0, 0};
void dfs(int x, int y, int k) {
    step[x][y] = k;  //记录到达(x,y)点的最短距离为k
    if (x == r && y == c) return ;  //搜到终点，提前结束本轮dfs
    for (int i = 0; i < 4; i++) {
        int nx = x + dx[i], ny = y + dy[i];
        // 确保新的路径走到点(nx,ny)的步数比之前step数组中存储的步数要小
        if (a[nx][ny] == '.' && k + 1 < step[nx][ny]) 
            dfs(nx, ny, k + 1);
    }
}
int main() {
    cin >> r >> c;
    for (int i = 1; i <= r; i++)
        for (int j = 1; j <= c; j++) {
            cin >> a[i][j];
            step[i][j] = INT_MAX;
        }
    dfs(1, 1, 1);
    cout << step[r][c];
    return 0;
}

说明：（1） int dx[]，创建一维数组时不写大小，程序会自动分析赋值的内容开辟空间。

（2） k + 1 < step[nx][ny]，此次的走法到达点(nx,ny)是k+1步，如果比之前某种最短的走法step[nx][ny]的步数更短，才选择这种走法。否则，不需要选择新的走法，选择之前最短的走法step[nx][ny]更好。

（3）在调用搜索函数dfs之前，记得给step数组的所有元素赋值为INT_MAX。

（4）调用dfs函数时，第三个参数初始应当给1，而不是0，是因为题目要求了起点也要计算步数。

（5）最终step[r][c]存放的就是从左上角(1,1)到(r,c)的最短步数。实际上，到任何一点（如果能走到）的最短步数都算出来了。