110. 平衡二叉树（简单）

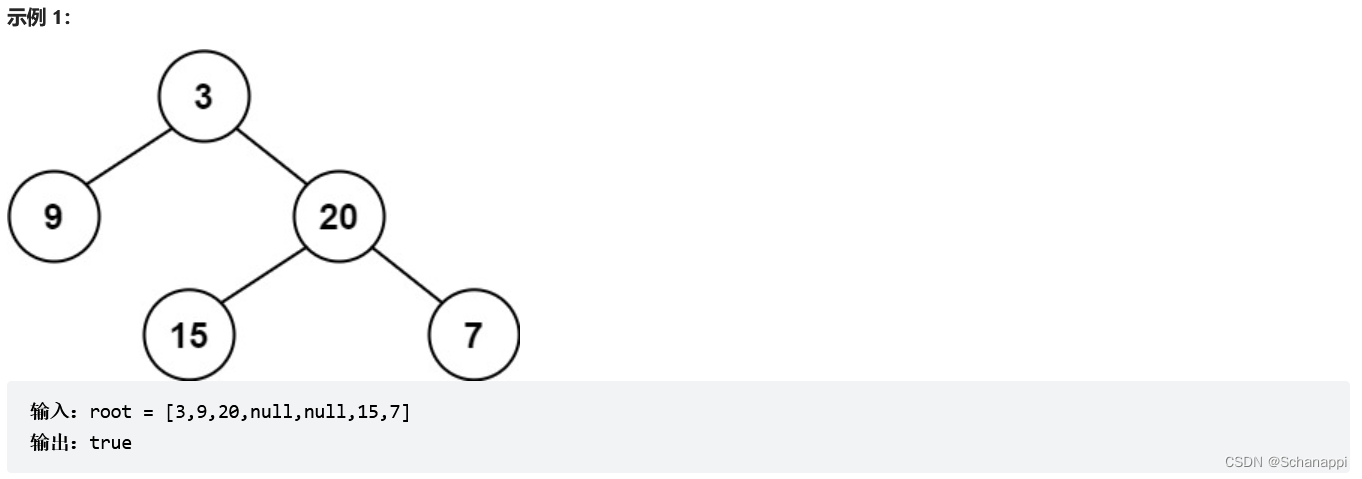
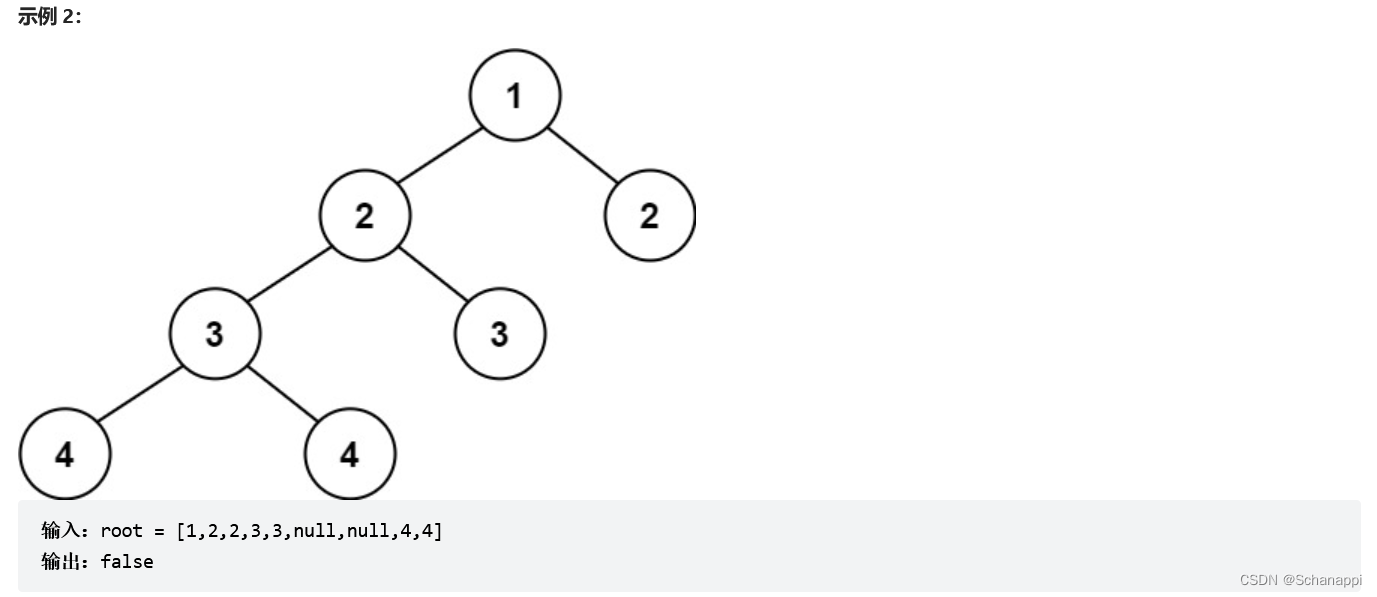
思路

• 对二叉树做先序遍历，从底至顶返回子树最大高度，若判定某子树不是平衡树则“剪枝”直接向上返回。

• 递归返回值：

  1. 当节点 root 左、右子树的高度差 > 1：返回 -1，代表此子树不是平衡树；
  2. 否则返回以节点 root 为根节点的子树的最大高度，即节点 root 的左、右子树中最大高度加1 ，(max(left，right) +1)。

• 递归终止条件：

  1. 当抵达叶子节点时，返回高度 0；
  2. 当左(右)子树高度 left/right == -1 时，代表此子树的左子树不是平衡树，因此直接返回 -1；

• isBalanced(root)：

  返回值: 若 helper(root) != 1 ，则说明此树平衡，返回 true ; 否则返回 false。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        // -1 表示不平衡
        return helper(root) != -1;
    }
    // 计算高度
    int helper(TreeNode* root){
        if(root == nullptr) return 0;
        int left = helper(root->left), right = helper(root->right);
        // -1 表示不平衡
        if(left == -1 || right == -1 || abs(left-right)>1){
            return -1;
        }
        // 返回子树的高度
        return max(left, right) + 1;
    }
};