最小生成树的扩展应用

AcWing 1146. 新的开始

利用虚拟源点建图和原题的题意是等价的，因此我们使用虚拟源点建图套最小生成树的模板

//虚拟源点

#include <iostream>
#include <cstring>

const int N = 310;

using namespace std;

int dist[N], w[N][N];
bool st[N];
int n;

int prime()
{
    int res = 0;
    memset(dist, 0x3f, sizeof dist);
    dist[0] = 0;//超级源点入队
    
    
    for(int i = 0; i < n + 1; i ++ )//循环n + 1次（有多少点循环多少次就行了，每次循环确定一条边）
    {
        int t = -1;
        for (int j = 0; j <= n; j ++ )
        {
            if (st[j] == 0 && (t == -1 || dist[t] > dist[j])) t = j;
        }
        
        st[t] = true;
        res += dist[t];
        for (int j = 0; j <= n; j ++ )
        {
            dist[j] = min(dist[j], w[t][j]);
            // if (dist[j] > w[t][j])//不知道为啥这样写不行
            // {
            //     dist[j] = w[t][j];
            // }
        }
    }
    return res;
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )
    {
        cin >> w[0][i];
        w[i][0] = w[0][i];//无向边（事实上最小生成树必须是无向边才可以用prime和kruskal，有向边的最小生成树目前还不知道怎么求）
    }
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            cin >> w[i][j];
            
    cout << prime();
    return 0;
}

AcWing 1145. 北极通讯网络

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;
#define x first
#define y second

const int N = 510;

struct Edge
{
    int a, b;
    double w;
    bool operator < (const Edge &t) const
    {
        return w < t.w;
    }
}e[N * N];

PII q[N];
int p[N];
int n, k;

double get_dist(PII a, PII b)
{
    int dx = a.x - b.x;
    int dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];//return x 会wa，必须return p[x]
}

int main()
{
    cin >> n >> k;
    
    for (int i = 0; i < n; i ++ ) p[i] = i;
    
    for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
    
    int m = 0;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < i; j ++ )//或者这样也行for (int j = 0; j < n && j != i; j ++ )
        {                           //如果j = i就会加入一条长度为0的边，必然影响我们对边的枚举
            e[m ++ ] = {i, j, get_dist(q[i], q[j])};
        }
        
    sort(e, e + m);
    
    int cnt = n;
    double res = 0;
    for (int i = 0; i < m; i ++ )
    {
        if (cnt <= k) break;
        int a = find(e[i].a), b = find(e[i].b);
        if (a != b)
        {
            p[a] = b;
            cnt -- ;
            res = e[i].w;
            
        }
    }
    
    printf("%.2lf", res);
    return 0;
}

AcWing 346. 走廊泼水节

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 6010;

struct Edge
{
    int a, b, w;
    bool operator < (const Edge &t) const
    {
        return w < t.w;
    }
}e[N];

int p[N], cnt[N];
int n, T;

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> T;
    while (T -- )
    {
        cin >> n;
        for (int i = 1; i <= n; i ++ ) p[i] = i, cnt[i] = 1;
        
        for (int i = 0; i < n - 1; i ++ )//边数为n - 1 因此循环 n - 1
        {
            int a, b, c;
            cin >> a >> b >> c;
            e[i] = {a, b, c};
        }
        
        sort(e, e + n - 1);//n - 1条边
        
        int res = 0;        
        for (int i = 0; i < n - 1; i ++ )
        {
            int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
            
            if (a != b)
            {
                res += (cnt[b] * cnt[a] - 1) * (w + 1);//完全图是每两点之间都有一条边，
                                                       //这里将除了当前的边的其它边都赋值为权值w + 1,
                                                       //这样可以保证每两点之间都有边，
                                                       //并且加完这些边之后还当前的最小生成树没有被改变且唯一
                                                       //（结构没被改变，权值和也没被改变）
                p[a] = b;//将a的所在的集合并入b
                cnt[b] += cnt[a];
                
            }
        }
        cout << res << endl;
    }
    return 0;
}

AcWing 1148. 秘密的牛奶运输

次最小生成树：有两种，一个是相同的权值，另一种是绝对次小生成树，权值是第二小的
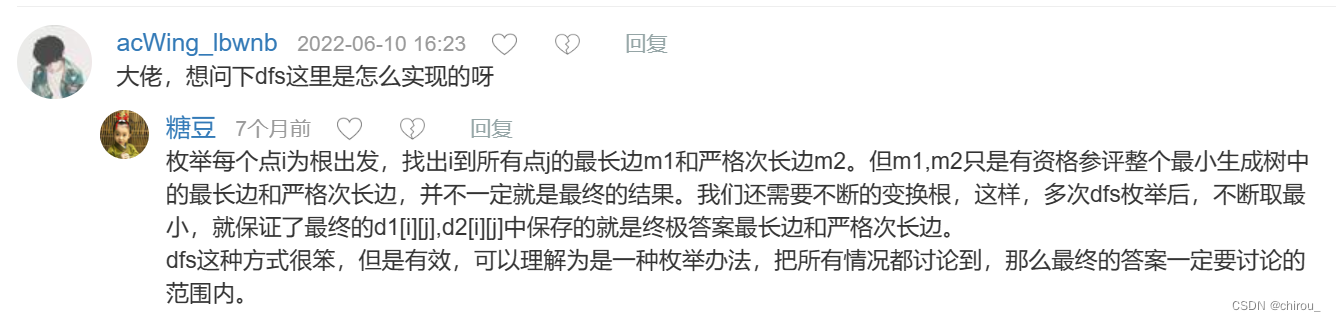
求次小生成树有两种方法：第二种方法比较全能
在这里插入图片描述
这题的dfs我是有点晕了，就因该weight是累加的才对呀

#include <iostream>
#include <algorithm>
#include <cstring>


using namespace std;
typedef long long LL;
const int N = 510, M = 1e4 + 10;

struct Edge
{
    int a, b, w;
    bool f;
    bool operator < (const Edge &t) const
    {
        return w < t.w;
    }
}edge[M];

int h[N], ne[N * 2], e[N * 2], idx, w[N * 2];//用来保存我们用kruskal计算的最小生成树，dfs的时候要用,最小生成树有n-1条边，又是无向边，因此是n * 2
int dist1[N][N], dist2[N][N];
int p[N];
int n, m;

void add (int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);                                                           
    return p[x];
}

void dfs(int s, int u, int fa, int mw1, int mw2)//s为起点，u为s的邻边，fa为上一个遍历的邻点用来防止回搜，mw1为最长路径，mw2为次长路径
{
    dist1[s][u] = mw1, dist2[s][u] = mw2;//收集上一层计算出来的结果
    
    for(int i = h[u]; ~i; i = ne[i])//本层探究u为起点到其他点的最长路径和次长路径
    {                               //但是我还是不知道为什么它要遍历邻边的邻边，
        int j = e[i], weight = w[i];
        if (j != fa)//防止回搜
        {
            int td1 = mw1, td2 = mw2;
            if (weight > td1) td1 = weight, td2 = mw1;
            else if (mw1 == mw2 || weight > mw2) td2 = weight;//else if(weight <= mw1 && weight > mw2)会wa不知道为啥
            
            dfs(s, j, u, td1, td2);                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       
        }
    }
}


int main()
{
    // cin >> n >> m;
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        // cin >> a >> b >> c;
        scanf("%d%d%d", &a, &b, &c);
        edge[i] = {a, b, c};
    }
    
    sort(edge, edge + m);
    for (int i = 1; i <= n; i ++ ) p[i] = i;
    
    
    LL sum = 0;//最小生成树的权值和
    //kruskal求最小生成树
    for (int i = 0; i < m; i ++ )
    {
        int a = edge[i].a, b = edge[i].b, w = edge[i].w;//因为a，b还要用，因此不能让 a = find(edge[i].a)
        int pa = find(a), pb = find(b);
        if(pa != pb)
        {
            p[pa] = pb;
            sum += w;
            add (a, b, w), add(b, a, w);
            edge[i].f = true;
        }
        
    }
    
    //以每个点为树的根节点搜索它到其它点的最长路径和次长路径，预处理好这些，方便我们后面给最小生成树“换边”
    for (int i = 1; i <= n; i ++ ) dfs(i, i, -1, 0, 0);
    //for (int i = 1; i <= n; i ++ ) dfs(i, -1, -1e9, -1e9, dist1[i], dist2[i]);
    
    LL res = 1e18;
    
    //遍历一遍所有边，找出不是生成树里面的边，
    //并尝试用它去替换生成树里面两点间的最长路径和次长路径
    //以此来找到次小生成树
    for (int i = 0; i < m; i ++ )
    {
        if (!edge[i].f)//如果该边不是最小生成树里面的边
        {
            int a = edge[i].a, b = edge[i].b, w = edge[i].w;
            LL t;
            if (w > dist1[a][b]) 
                t = sum + w - dist1[a][b];
            else if (w > dist2[a][b]) 
                t = sum + w - dist2[a][b];
            
            res = min(res, t);
        }
    }
    
    printf("%lld\n", res);
    return 0;
}