引言

上一节介绍了受限玻尔兹曼机中随机变量节点的后验概率，本节将介绍随机变量结点的边缘概率。

回顾：场景构建

已知受限玻尔兹曼机示例表示如下：

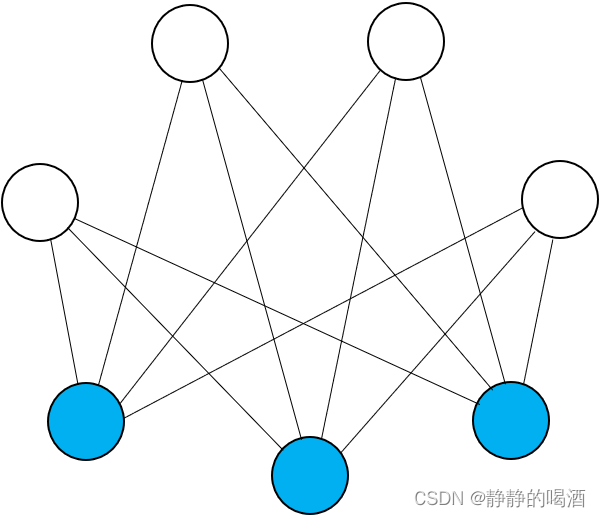
将随机变量集合$\mathcal{X}\in {\mathbb{R}}^p$分成观测变量$v$和隐变量$h$两个部分：
$$\mathcal{X}=(x_1,x_2,\cdots ,x_p{)}^T={\left(\begin{array}{c}h\\ v\end{array}\right)}_{p\times 1}\{\begin{array}{l}h=(h_1,h_2,\cdots ,h_m{)}_{m\times 1}^T\\ v=(v_1,v_2,\cdots ,v_n{)}_{n\times 1}^T\end{array}m+n=p$$
并且观测变量$v$、隐变量$h$中的每一个随机变量均服从伯努利分布：
h j ( j = 1 , 2 , ⋯   , m ) ∈ { 0 , 1 } v i ( i = 1 , 2 , ⋯   , n ) ∈ { 0 , 1 } \begin{aligned} h_j(j=1,2,\cdots,m) \in \{0,1\} \\ v_i (i=1,2,\cdots,n) \in \{0,1\} \end{aligned} hj​(j=1,2,⋯,m)∈{0,1}vi​(i=1,2,⋯,n)∈{0,1}​
基于该模型，随机变量集合$\mathcal{X}$的联合概率分布表示如下：
P ( X ) = P ( v , h ) = 1 Z exp ⁡ { − E ( h , v ) } = 1 Z exp ⁡ ( v T W h + b T v + c T h ) = 1 Z exp ⁡ [ ∑ j = 1 m ∑ i = 1 n v i ⋅ w i j ⋅ h j + ∑ i = 1 n b i v i + ∑ j = 1 m c j h j ] \begin{aligned} \mathcal P(\mathcal X) = \mathcal P(v,h) & = \frac{1}{\mathcal Z} \exp \{- \mathbb E(h,v)\} \\ & = \frac{1}{\mathcal Z} \exp \left(v^T\mathcal W h + b^Tv + c^Th\right) \\ & = \frac{1}{\mathcal Z} \exp \left[\sum_{j=1}^m\sum_{i=1}^n v_i \cdot w_{ij} \cdot h_j + \sum_{i=1}^n b_i v_i + \sum_{j=1}^m c_j h_j\right] \end{aligned} P(X)=P(v,h)​=Z1​exp{−E(h,v)}=Z1​exp(vTWh+bTv+cTh)=Z1​exp[j=1∑m​i=1∑n​vi​⋅wij​⋅hj​+i=1∑n​bi​vi​+j=1∑m​cj​hj​]​

推断任务——边缘概率求解

• 在受限玻尔兹曼机中，仅对观测变量$v$的边缘概率分布进行求解。边缘概率$\mathcal{P}(v)$本质上就是对联合概率分布关于隐变量$h$的积分操作：
  $$\mathcal{P}(v)=\sum _h\mathcal{P}(v,h)$$
• 由于模型已知，即模型参数$\mathcal{W},b,c$是已知的。将上式沿$\mathcal{P}(v,h)$展开：
  再写一遍~
化简目标是：将$\mathcal{P}(v,h)$中关于隐变量$h$中的项积分掉，使其变为‘仅包含观测变量’$v$的式子。
  $$\begin{array}{rl}\mathcal{P}(v)& =\sum _h\left[\frac{1}{\mathcal{Z}}\exp \left(\sum _{j=1}^m\sum _{i=1}^n{v}_i\cdot w_{ij}\cdot h_j+\sum _{i=1}^n{b}_i{v}_i+\sum _{j=1}^m{c}_j{h}_j\right)\right]\\ & =\sum _{h_1},\cdots \sum _{h_m}\left[\frac{1}{\mathcal{Z}}\exp \left(\sum _{j=1}^m\sum _{i=1}^n{v}_i\cdot w_{ij}\cdot h_j+\sum _{i=1}^n{b}_i{v}_i+\sum _{j=1}^m{c}_j{h}_j\right)\right]\end{array}$$
• 观察上述中括号内的项，其中$\frac{1}{\mathcal{Z}},{\sum }_{i=1}^n{b}_i{v}_i$与随机变量$h_j(j=1,2,\cdots ,m)$无关；因而将它们提到公式前端：
  为了方便观看，将$v_i(i=1,2,\cdots ,n)$的部分进行合并
  $$\begin{array}{rl}\mathcal{P}(v)& =\frac{1}{\mathcal{Z}}\exp (b^{T}v)\cdot \sum _{h_1},\cdots ,\sum _{h_m}\exp \left\{\sum _{j=1}^m\left[(h_j{\mathcal{W}}_j{)}^{T}v+c_j{h}_j\right]\right\}\\ & =\frac{1}{\mathcal{Z}}\exp (b^{T}v)\cdot \sum _{h_1},\cdots ,\sum _{h_m}\exp \left\{[(h_1{\mathcal{W}}_1{)}^{T}v+c_1{h}_1]+\cdots +(h_m{\mathcal{W}}_m+c_m{h}_m{)}^{T}v\right\}\end{array}$$
  以大括号第一项为例：$(h_1{\mathcal{W}}_1{)}^{T}v+c_1{h}_1$中只和隐变量$h_1$相关，与其他隐变量无关。因此，上式可改写为：
  $$\mathcal{P}(v)=\frac{1}{\mathcal{Z}}\exp (b^{T}v)\cdot \left\{\sum _{h_1}\exp [(h_1{\mathcal{W}}_1{)}^{T}v+c_1{h}_1]\right\}\cdots \left\{\sum _{h_m}\exp [(h_m{\mathcal{W}}_m{)}^{T}v+c_m{h}_m]\right\}$$
  由于 h j ( j = 1 , 2 , ⋯   , m ) ∈ { 0 , 1 } h_j(j=1,2,\cdots,m) \in \{0,1\} hj​(j=1,2,⋯,m)∈{0,1}，因此上式每个大括号中的项可继续展开，表示为如下形式。这里以第一项为例：
  ∑ h 1 exp ⁡ [ ( h 1 W 1 ) T v + c 1 h 1 ] = ∑ h 1 ∈ { 0 , 1 } exp ⁡ [ ( h 1 W 1 ) T v + c 1 h 1 ] = exp ⁡ ( 0 ) + exp ⁡ ( W 1 T v + c 1 ) = 1 + exp ⁡ ( W 1 T v + c 1 ) \begin{aligned} \sum_{h_1} \exp [(h_1\mathcal W_1)^Tv + c_1h_1] & = \sum_{h_1 \in \{0,1\}}\exp [(h_1\mathcal W_1)^Tv + c_1h_1] \\ & = \exp(0) + \exp(\mathcal W_1^Tv + c_1) \\ & = 1 + \exp(\mathcal W_1^Tv + c_1) \end{aligned} h1​∑​exp[(h1​W1​)Tv+c1​h1​]​=h1​∈{0,1}∑​exp[(h1​W1​)Tv+c1​h1​]=exp(0)+exp(W1T​v+c1​)=1+exp(W1T​v+c1​)​
  对上式继续化简：
  对$1+\exp ({\mathcal{W}}_j^{T}v+c_j)$进行变形，将$log$函数引入,从而使$\exp ,\log$相互抵消。
  $$1+\exp ({\mathcal{W}}_j^{T}v+c_j)=\exp \left\{\log [1+\exp ({\mathcal{W}}_j^{T}v+c_j)]\right\}j=1,2,\cdots ,m$$
• 因而原式$\mathcal{P}(v)$有:
  $$\mathcal{P}(v)=\frac{1}{\mathcal{Z}}\exp (b^{T}v)\cdot \prod _{j=1}^m\exp \left\{\log [1+\exp ({\mathcal{W}}_j^{T}v+c_j)]\right\}$$
  将$exp$提出来，最终有：
  $$\mathcal{P}(v)=\frac{1}{\mathcal{Z}}\exp \left\{b^{T}v+\sum _{j=1}^m\log [1+\exp ({\mathcal{W}}_j^{T}v+c_j)]\right\}$$
  观测变量$v$的边缘概率分布即为所求。

边缘概率与Softplus函数

观察上式中的$\log [1+\exp ({\mathcal{W}}_j^{T}v+c_j)]$部分，它实际上就是softplus的表现形式：
$$\text{Softplus}(x)=\log [1+\exp (x)]$$
$\text{Softplus}$函数图像表示如下：

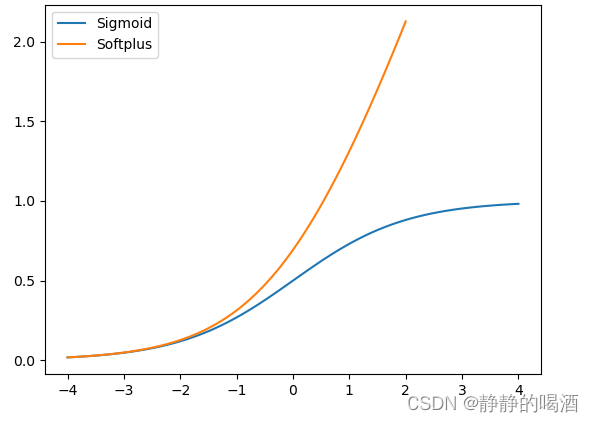
Softplus也是一种激活函数，它可看做是ReLU函数的平滑效果，其值域为$(0,\infty )$(不含0)。并且不会像ReLU函数产生神经元挂掉情况。
并且更值得一提的属性是，Softplus函数的导数是Sigmoid函数：
$$\begin{array}{rl}\frac{\partial \text{ Softplus}(x)}{\partial x}& =\frac{\exp (x)}{\exp (x)+1}\\ & =\frac{1}{1+\frac{1}{\exp (x)}}\\ & =\frac{1}{1+\exp (-x)}\end{array}$$

因而上述公式可最终化简为：
${\mathcal{W}}_j$表示$\mathcal{W}$矩阵第$j$行的行向量。
P ( v ) = 1 Z exp ⁡ { b T v + ∑ j = 1 m Softplus ( W j T v + c j ) } \mathcal P(v) = \frac{1}{\mathcal Z} \exp \{b^Tv + \sum_{j=1}^m \text{Softplus}(\mathcal W_j^T v + c_j)\} P(v)=Z1​exp{bTv+j=1∑m​Softplus(WjT​v+cj​)}

至此，受限玻尔兹曼机介绍结束(Learning问题的坑后续补)。下一节将介绍配分函数(Partition Function)。

相关参考：
机器学习-受限玻尔兹曼机（6）-模型推断（Inference）-边缘概率
速用笔记 | Sigmoid/Tanh/ReLu/Softplus 激活函数的图形、表达式、导数、适用条件