（1）是什么？

是一种适用于关键字较多的情况下的排序算法，例如在十亿个数中选出前1000个最大值或者最小值
如果在传统的排序算法中（例如冒泡，插入等），我们习惯把目标数据整体进行一次排序，再截取出前1000个最小的或者最大的。
但是我们可以设想一下，从一开始我们目标就只要1000个，那么其实其余九亿九千九百九十九万九千个数据，我们压根不需要知道它们的排序顺序，只需要知道它们都比我们1000个目标数据中最大值都要大就可以了
这就是堆排序。

它的思想整体上非常清晰简单，结构上是一个完全二叉树。
根结点比左右孩子都大则叫做大根堆。其中，左右孩子的根结点，又会比它们的左右孩子都大。
根结点比左右孩子都小则叫做小根堆。其中，左右孩子的根结点，又会比它们的左右孩子都小。
更简单点说：所有中间结点，一定比它孩子大（大根堆），或者一定比它的孩子小（小根堆）

（2）如何构建大根堆

初始化：

1:按照给出的数组，首先按照层次优先（逐层摆放）构造一棵二叉树
2:从该二叉排序树的最后一个叶子结点的根结点出发，比较该结点的左右孩子，选取最大的置换到根结点上
3:整理倒数第二非叶子结点，比较并选择一个最大的置换到根结点…
4:依次类推，直到整理完整棵树，此时树的根结点一定是该大根堆中最大值
5:在把大数往上顶的过程中，也要看互换位置的数是否比左右孩子都大，如果不是，则又要选择一个最大的换到该子树根结点。

例如：假设有数组【1，3，5，7，9，2，4，6，8，10】要求建立大根堆

1:先按照层次优先原则建立二叉树（该树生成后默认按照行遍历存放在一个一维数组中，且该数组下标从1开始，即下标为1存放着根结点1，下标2存放左孩子2，下标3存放着右孩子5，以此类推）

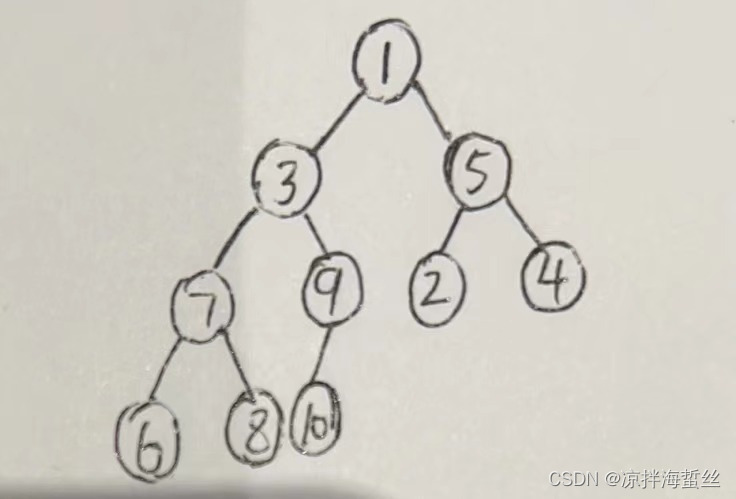
2:从该二叉树的最后一个非叶子结点出发，比较该结点的左右孩子，选取最大的置换到根结点上
如何找到二叉树最后一个非叶子结点：n/2向下取整
该例子中，10个元素，则10/2 = 5；即最后一个非叶子结点下标是5，也就是根结点值为9的子树。
比较9，10，发现10最大，于是10和9交换位置。

3:整理倒数第二非叶子结点，比较并选择一个最大的置换到根结点…
如何找到倒数第二个非叶子结点：n/2 - 1 = 4
也就是下标为4的，根结点值为7的子树
比较6，7，8，于是7和8交换位置，8作为根结点。

4:依次类推，直到整理完整棵树，此时树的根结点一定是该大根堆中最大值
5:在把大数往上顶的过程中，也要看互换位置的数是否比左右孩子都大，如果不是，则又要选择一个最大的换到该子树根结点。

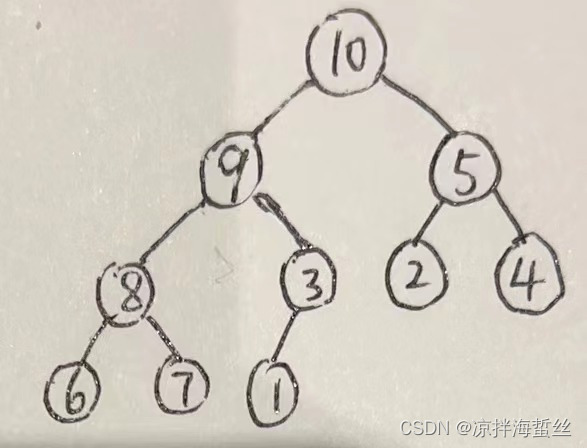
到这里就完成了大根堆的构建

输出栈顶元素：

当输出栈顶的10后，固定用【最后一个叶子结点】1补上，发现1破坏了大根堆的性质，于是要从根结点往下调整，也就是比较1，9，5；把9放根结点。
1下沉到左子树根结点，但是还是不满足大根堆性质，于是比较1，8，3；把8放到左子树根结点，1再次下沉到左子树的左子树的根结点中
比较1，6，7；把7替换到左子树的左子树的根结点，把1再次下沉。
至此，重新调整的二叉树又符合大根堆性质了。

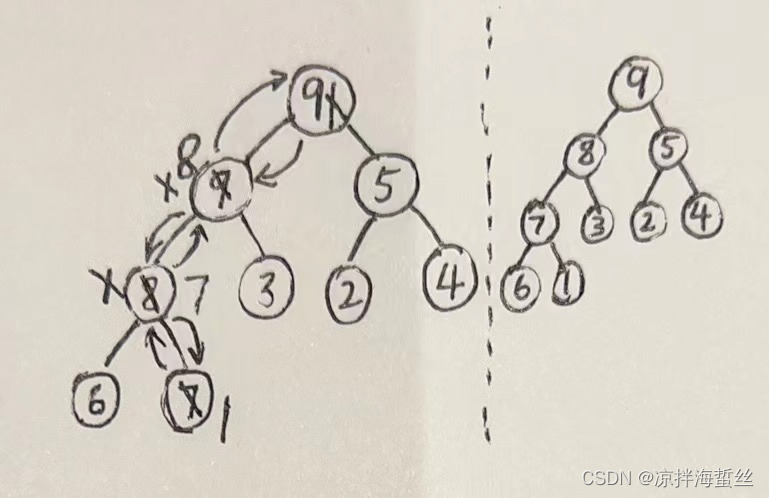
新增/插入元素操作：

新增/插入的元素都是把新结点放在新生成的最后一个叶子结点中，然后比较该新叶子结点数据的值与它父结点的值的大小，看是否需要换位置，如果需要，则开始调整，这跟初始化时候一样的操作。

⚠️注意，初始化和新增元素都是由下至上的调整，而删除了栈顶元素，是由上至下的调整。

代码实现：

#include <stdio.h>

void HeapSort(int a[], int i, int lenght){
	/*用以保存子树的根结点*/
	a[0] = a[i];
	/* 按照二叉树性质，不断i*2是不断深入找到下一层的左孩子结点 */
	for(int j=i*2; j<=lenght; j=j*2){
		/* k是对应子树的右孩子结点，先比较右孩子 */
		int k = j+1; 
		/* 左右孩子比较出一个大值 */
		if(k<lenght && a[k]>a[j]){
			j = k;
		}
	    /* 判断根结点与左右孩子的最大值谁更大 */
		if(a[0]<a[j]){
			a[i] = a[j];
			i = j;
		}
	}
	/* 循环退出后，j一定是最适合temp值的地方 */
	a[i] = a[0];
}

int main()
{
	int a[]={0,1,3,5,7,9,2,4,6,8,10};
	int lenght = 11;
	/* 从下往上逐个非叶子结点调整 */
	for(int i=lenght/2; i>0; i--) {
		HeapSort(a,i,lenght);
	}
   
   return 0;
}