输出形式

李宏毅讲到：

• 模型的输入是只有一种形式——词向量
• 但是输出的形式却是不唯一的，主要有以下三种：
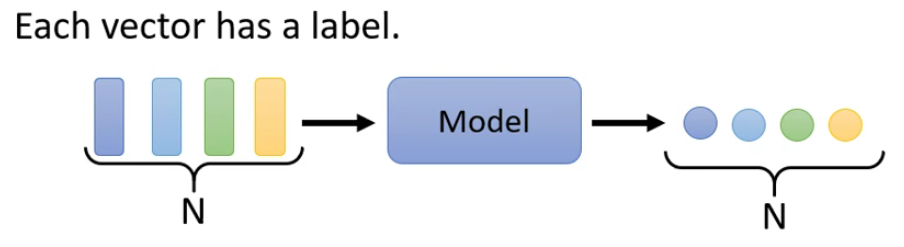
  • 每一个向量对应一个输出(多对多，且一一对应)
    • 
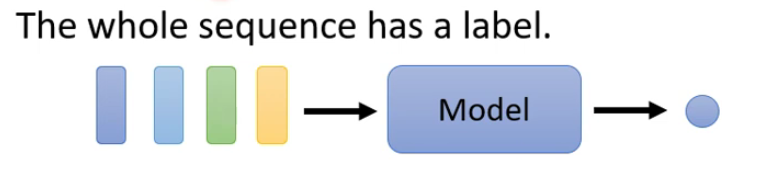
  • 每个序列只有一个输出(多对一)
    • 
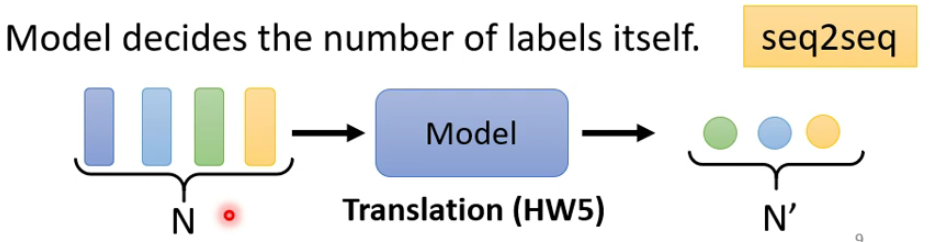
  • 一个序列对应一个序列(多对多，长度不确定)
    • 

---

自注意力机制引入

[这里以第一种形式来做说明，什么是self-attention]

考虑这样的一个例子：词形标注怎么做？

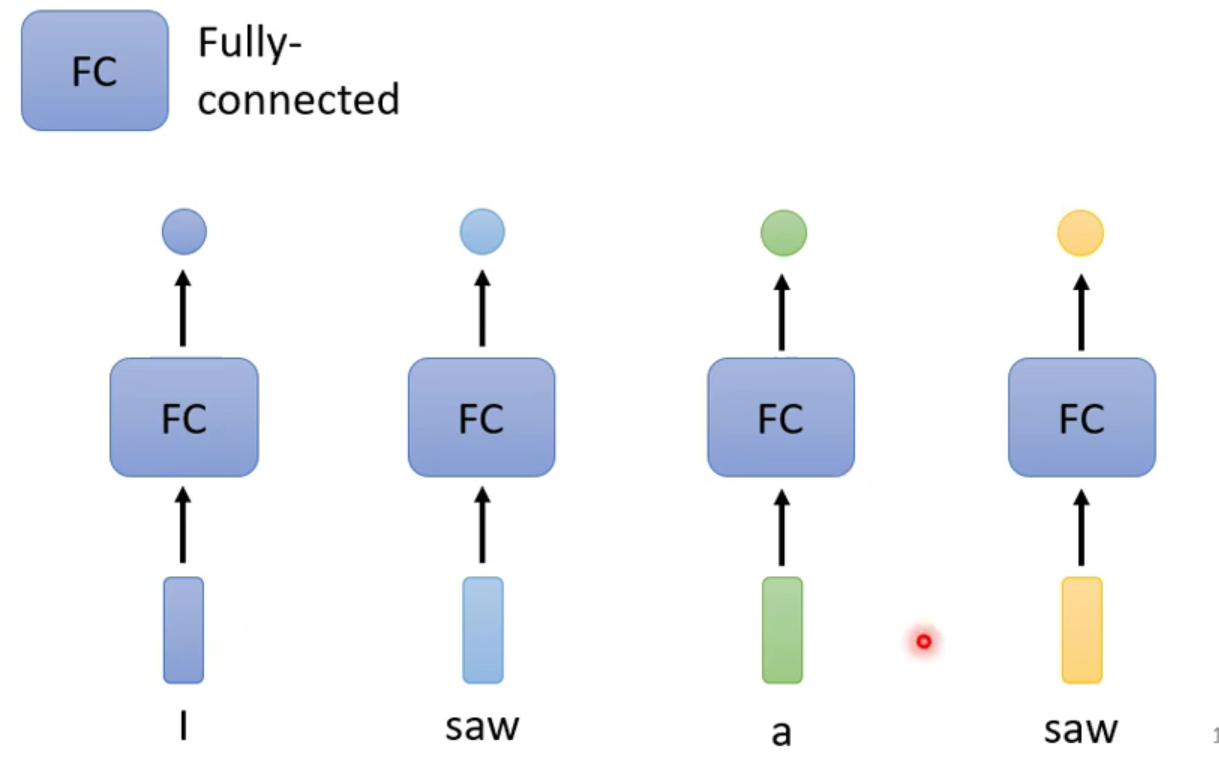
第一阶段

首先想到的是，也是最容易想到的是，一个个对应输出，但是这样存在一个大问题就是词与词之间是没有关系的，也就是说上图中的第一个saw和最后一个saw的词形输出是相同的，这显然是不对的，那么该怎么处理呢？

第二阶段

既然在第一阶段中突出的一个问题就是没有办法考虑词在全文中的信息，那么我们可不可以将所有的信息连接起来呢，这样的处理方法就是，加入一个window窗口机制，这样每次就只处理一个窗口大小的数据就可以了，效果如下：

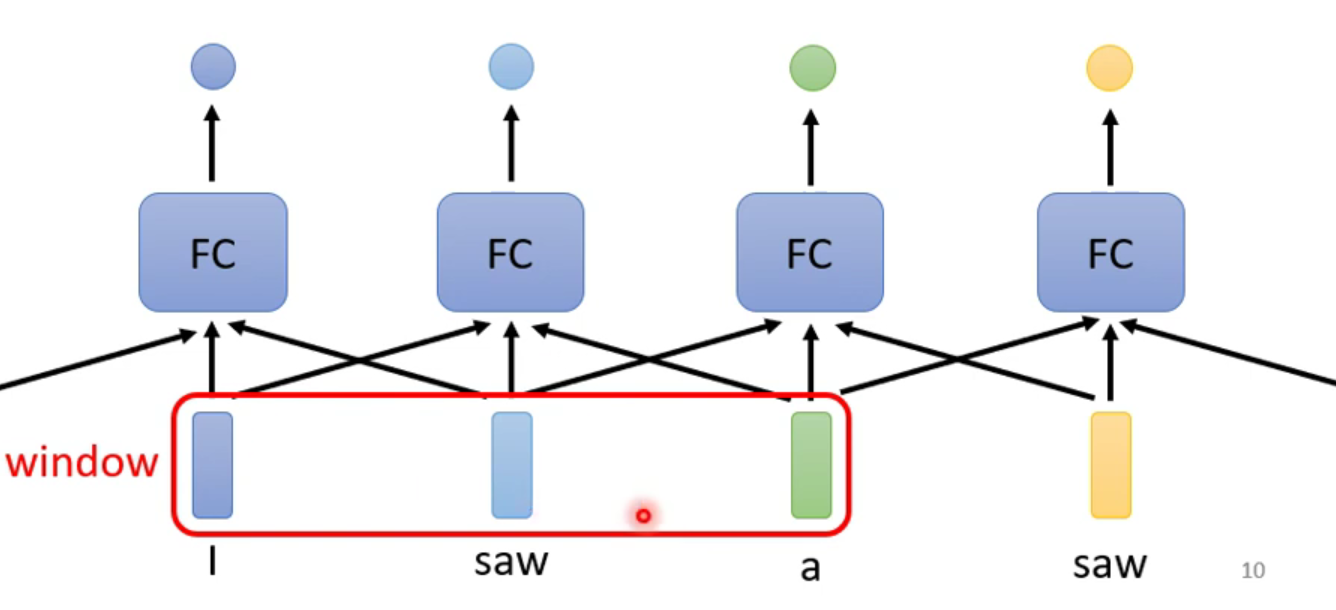
但是这样还存在以下几个问题就是：

1. 在一个句子中，窗口的大小怎么确定？
2. 对于整个句子来说该怎么用窗口来覆盖？
3. 句子的长度也不是唯一的，是动态变化的，那么该怎么确定这个窗口大小呢？

第三阶段(引入self-attention)

self-attention机制是可以根据你输入的长度来自动确定输出的长度，示意图如下：

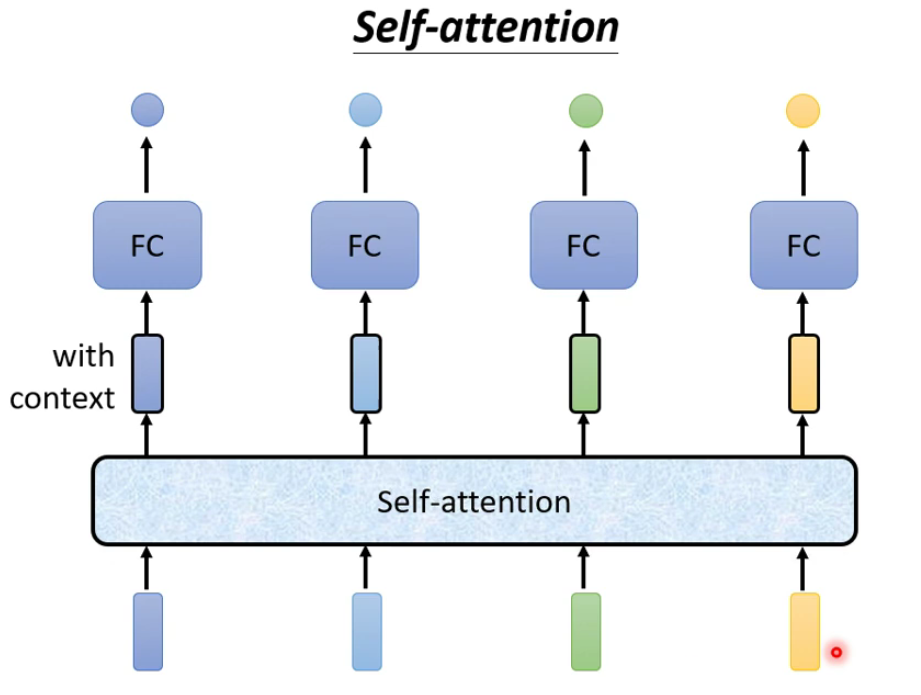
当然，self-attention是可以叠加的，这样的话就可以更好的输出我们想要的结果：

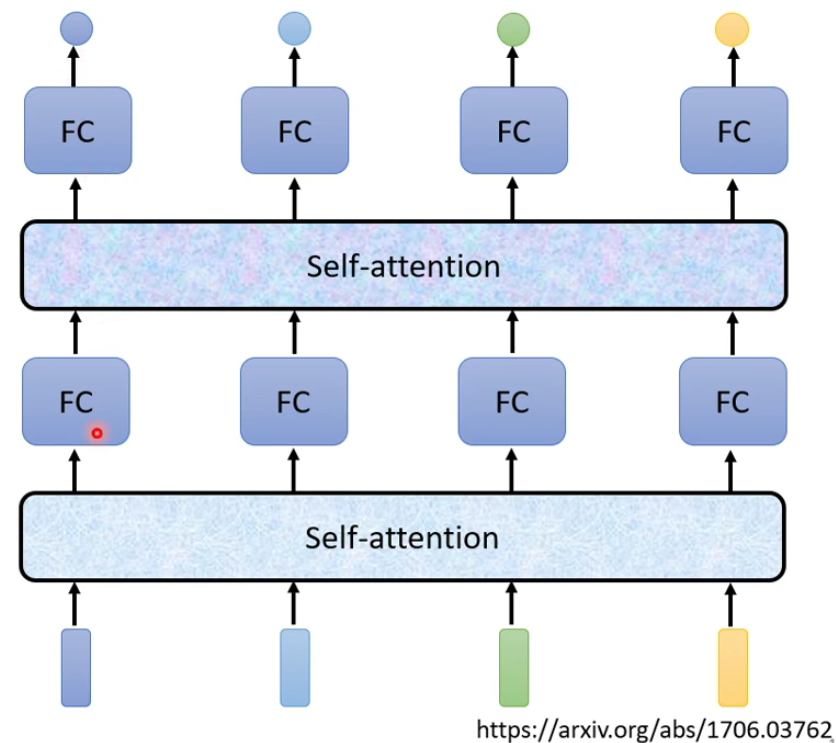
[有关self-attention最重要的一篇文章就是transformer的提出——《Attention is all you need》]

---

自注意力机制的原理

最重要的机制就是要看self-attention到底是怎么实现的：

---

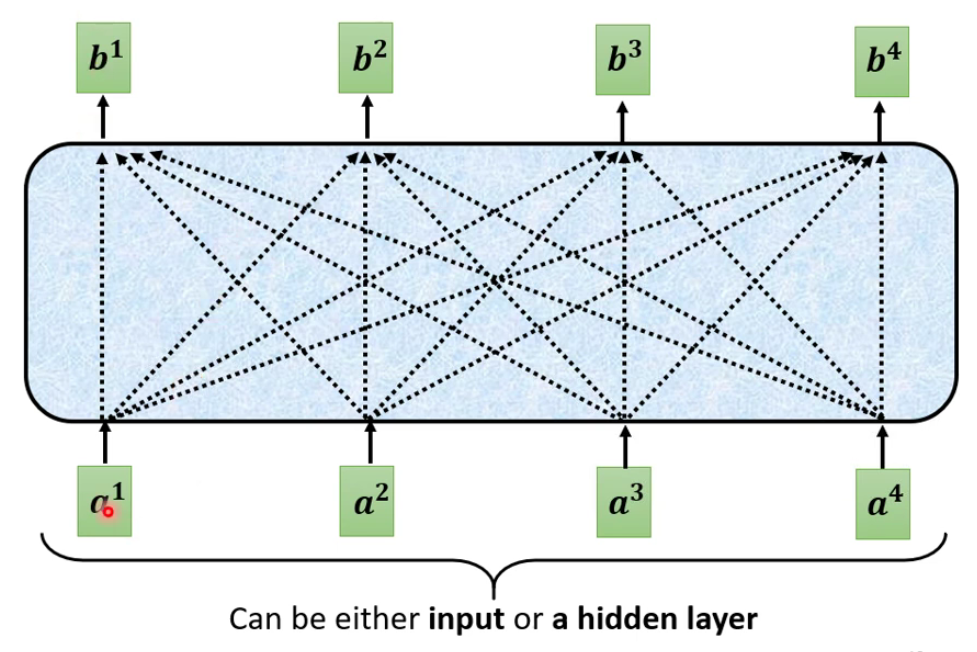
相关性

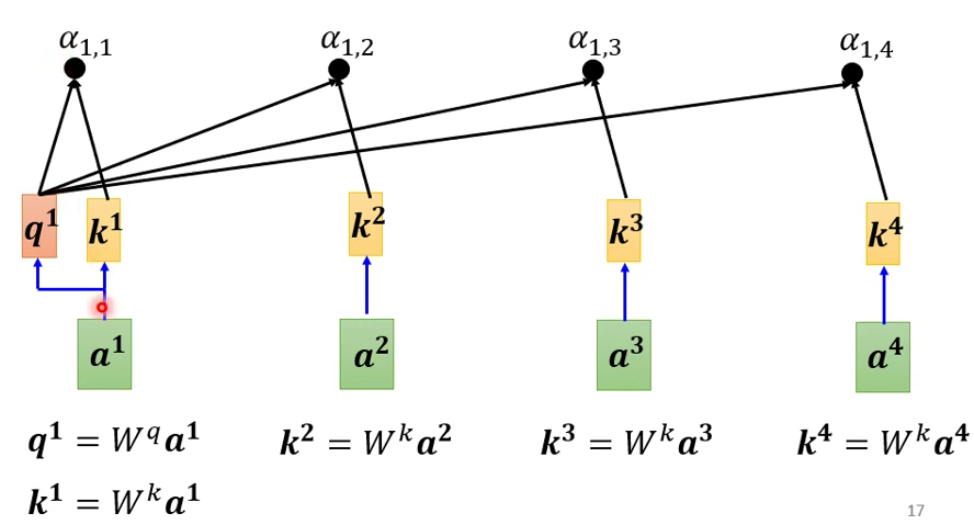
我们先以如何产生$b^1$​来说明这个self-attention机制的：

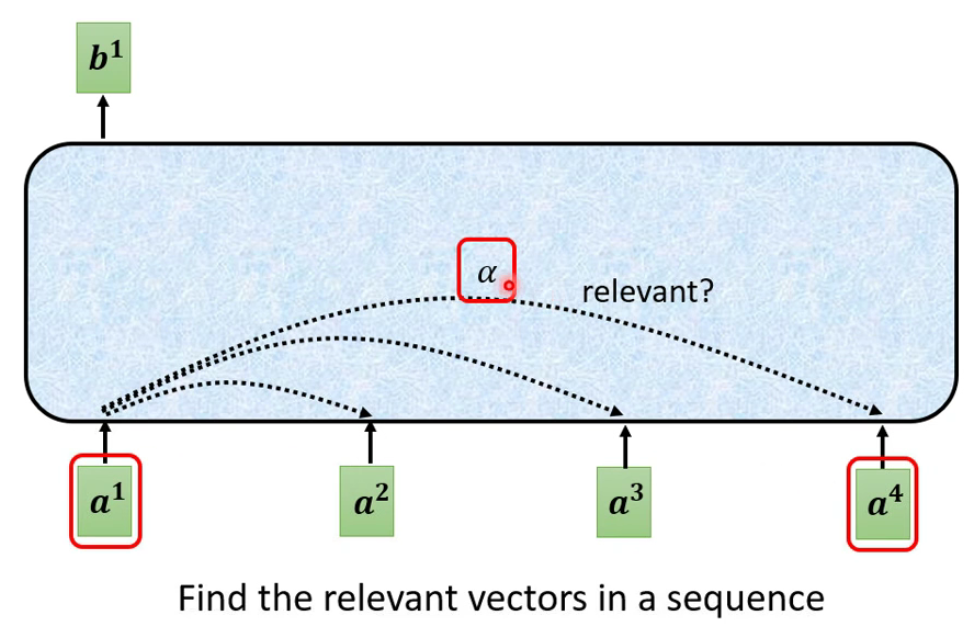
首先就是判断或者说找到输入序列之间的关系/相关性(这一步的作用就是找到那个整个sequence里面，哪些向量是重要的，哪些是不重要的)。

为了解释方便，这里用$\alpha$表示向量之间的相关性。

---

attention模块

这里就需要对上述的$\alpha$的如何计算做一个说明了，常用的就是Dot-product(transformer里面也是用的这个)。当然还有Additive，这两种方法都是根据输入的两个向量，然后分别对应相乘两个不同的矩阵来做一个运算而得到最后的$\alpha$。

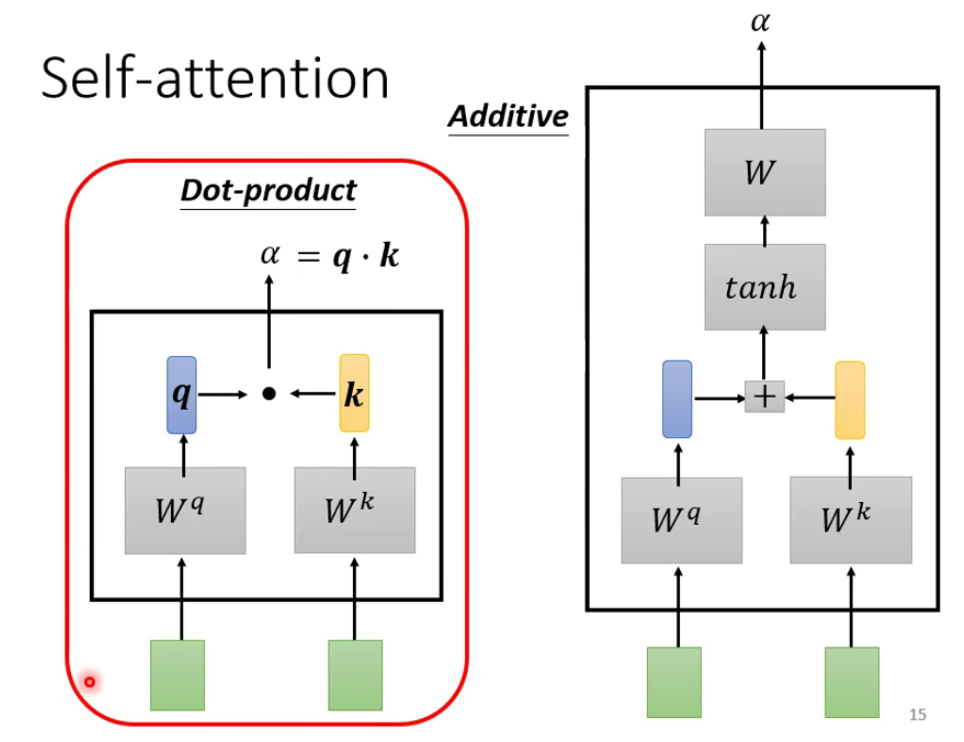
从宏观的角度

那么如何将上面讲到的东西整合一下呢，或者说整合的过程是什么样子的呢？

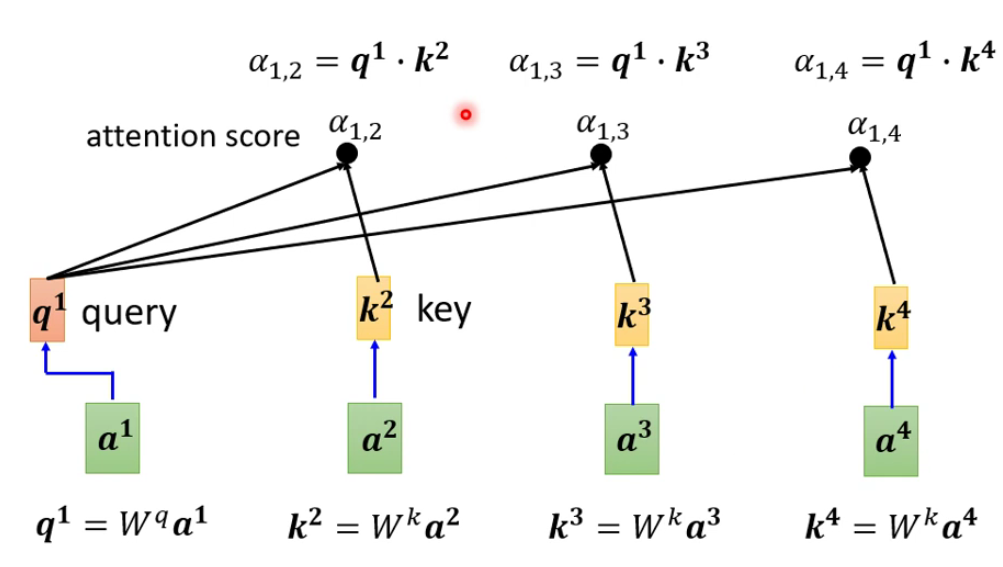
• query这个单词的意思就是我们想要查询的向量(也就是要查询的内容)，故用单词query来表示，简称为q。
• key相当于关键字，也就是说相对于要查询的向量的，其他的向量就是看成query的关键字key。
• 其实上述的过程就是找与$q^1$相关的k

---

当然在实际使用的过程中，还会有自己跟自己的匹配，至于有什么用，还不清楚：

最后再通过一个soft-max层作为输出最后$\alpha$输出，当然也可以不用soft-max作为输出，看自己怎么选择：

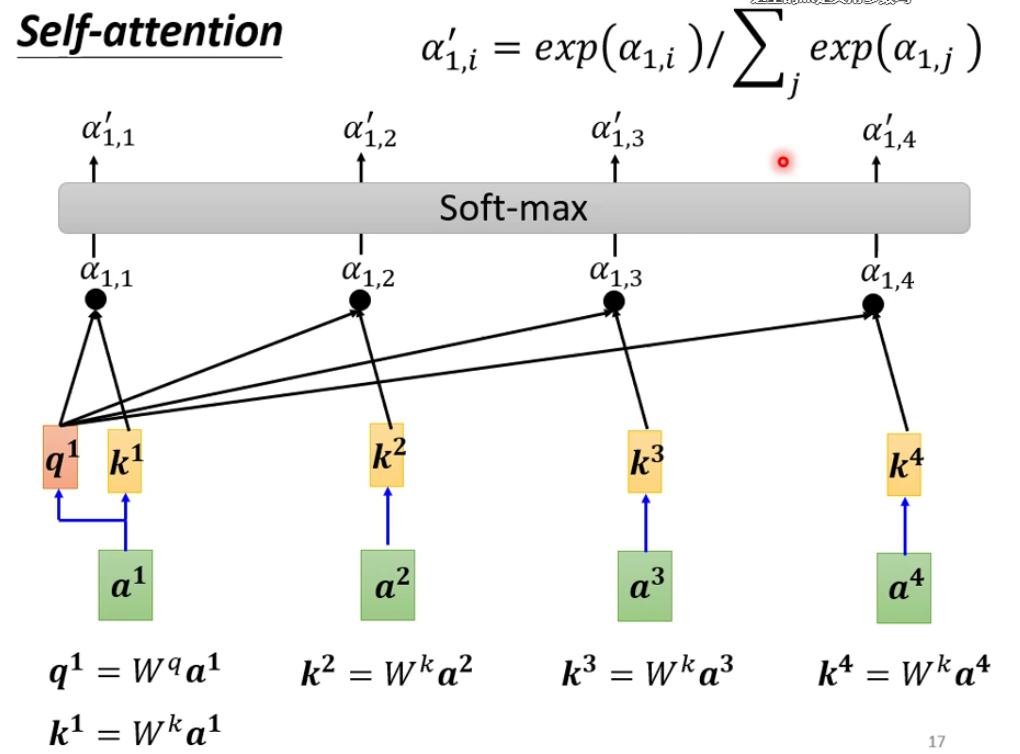
我们得到了这个$\alpha$之后还需要做最后的运算——得到我们的预测输出$b^2$：

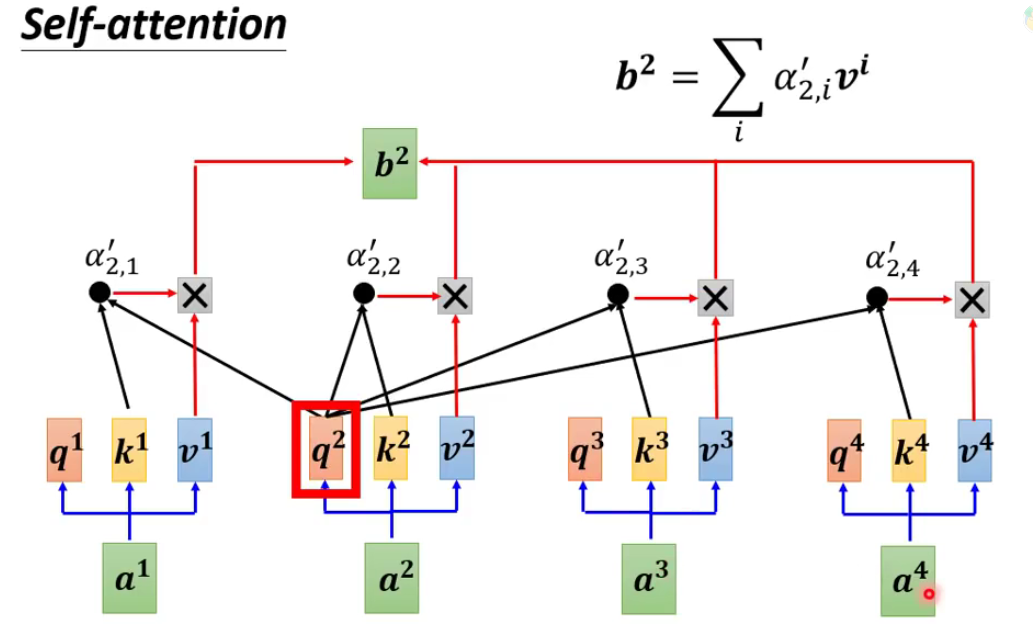
从上图可以看出，对于输入的一个向量总共是有三个参数需要输出并进行运算的，分别是$q^i,k^i,v^i$。

从矩阵运算的角度

其实我们细化一下来考虑，就是将向量的运算全部用矩阵来代替实现的：

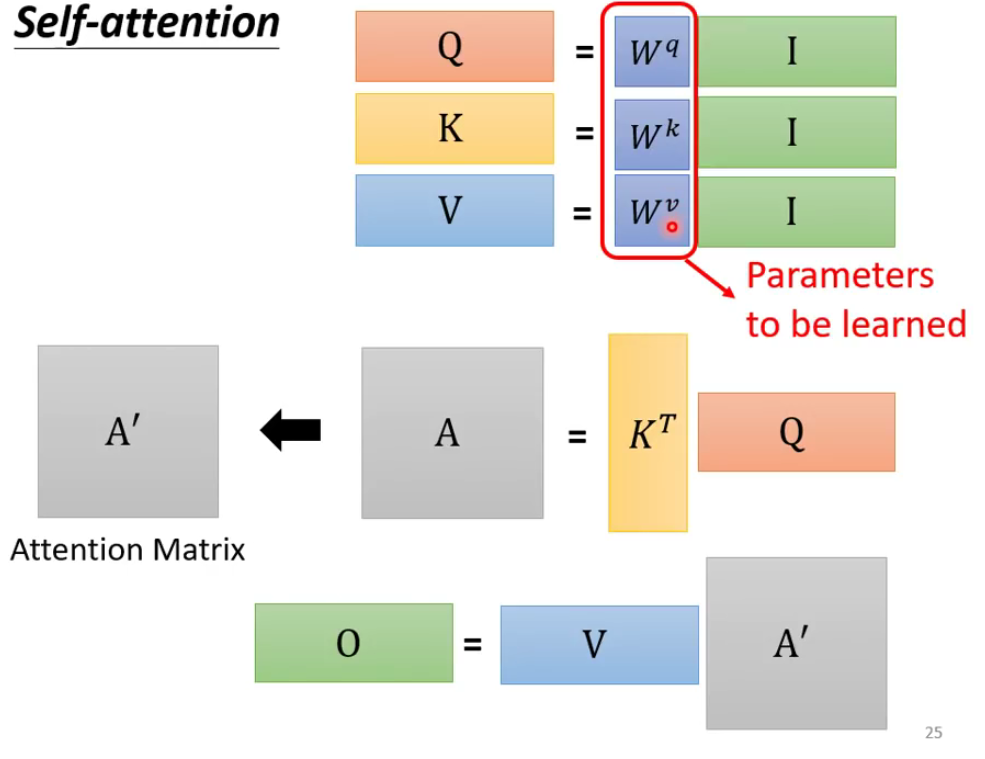
• 从输入a得到QKV

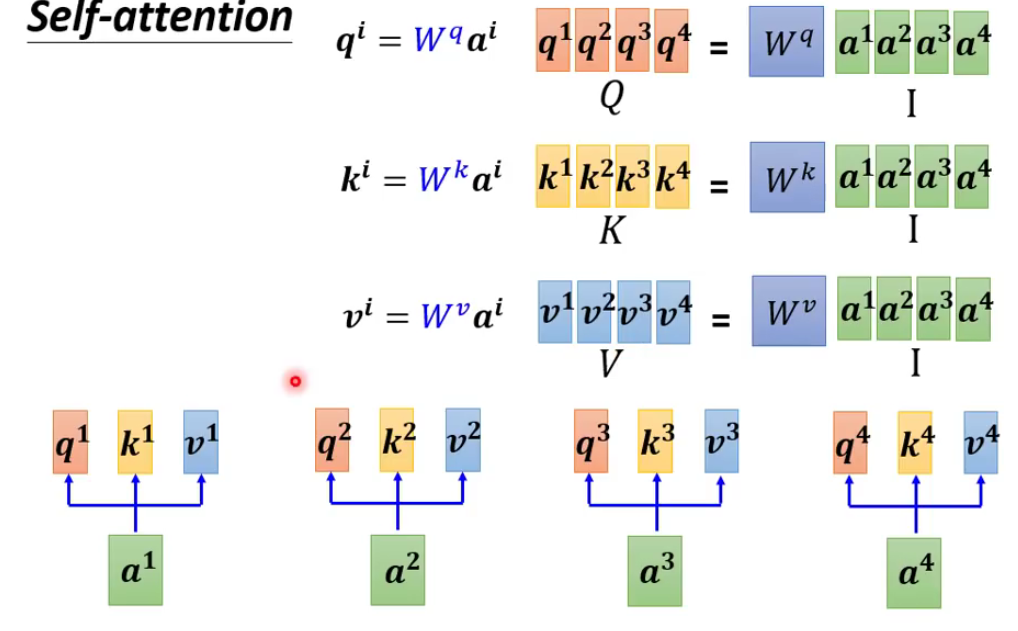
[上图也可以用《神经网络与深度学习》P204的图来表示]

• 从KQ得到softmax

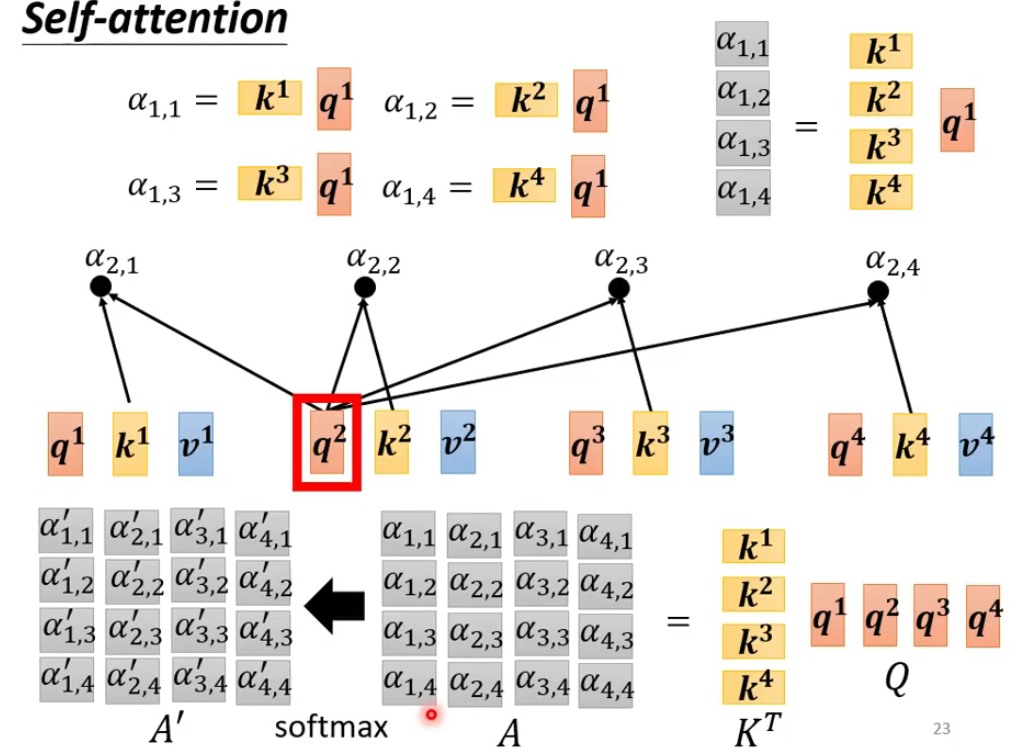
• 从softmax，V到输出

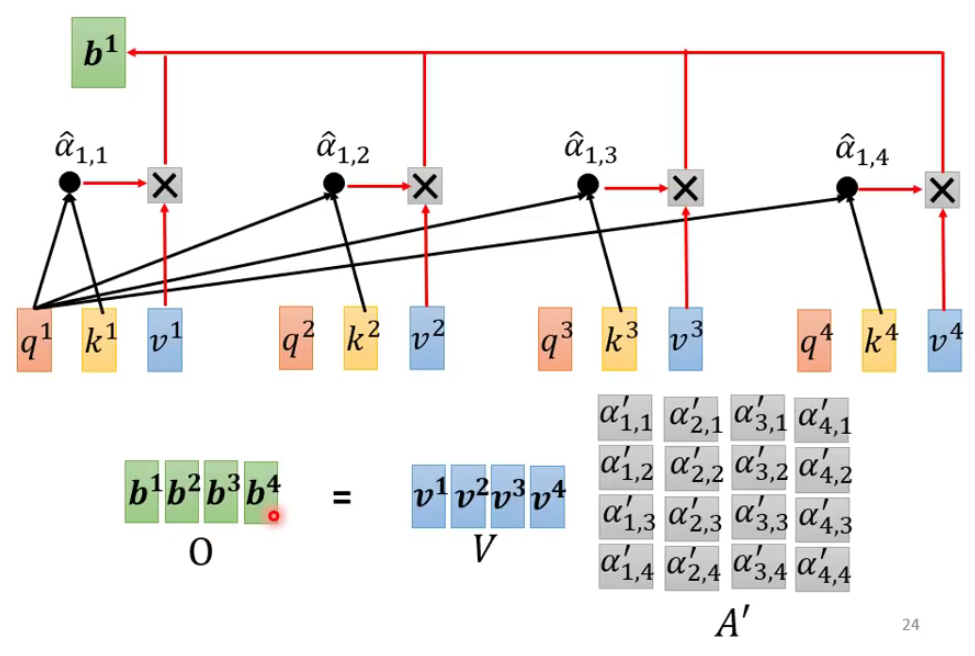
• 总结如下：

字注意力机制的改进

多头自注意力机制

2头自注意力机制为例，那么如何实现呢？是什么意思呢？看下图就知道了。

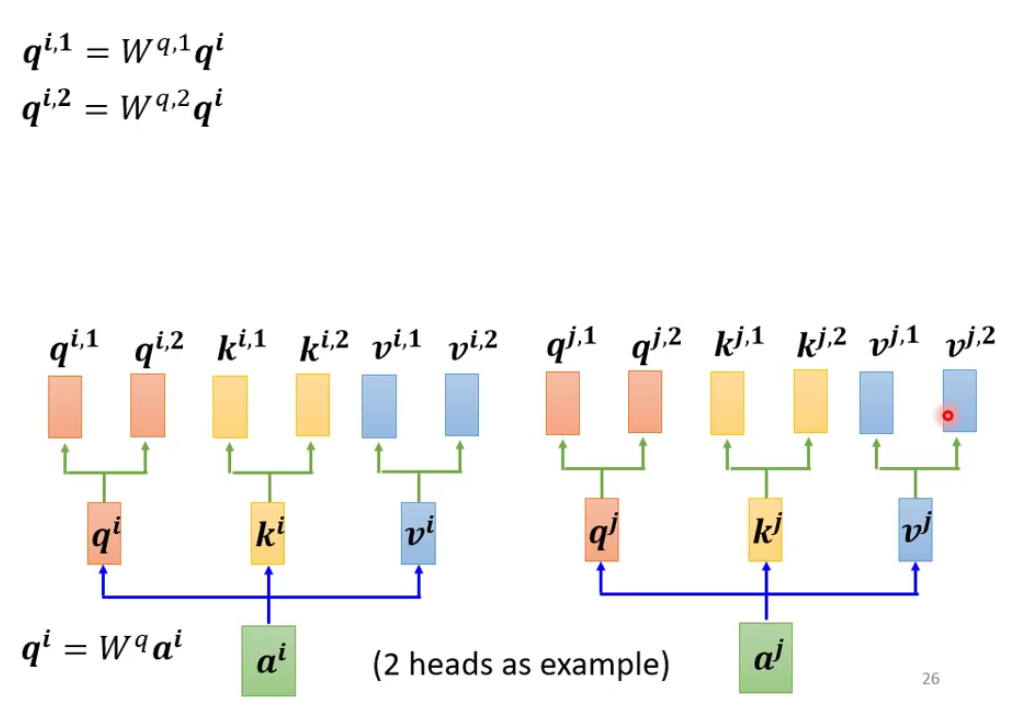
如上图所示，就是在计算完成qi的时候，再去对应相乘两个不同的矩阵，这样就得到了新的向量。

其中$q^{i,1}$表示第i个元素的第1个向量

---

那么如何做注意力的运算呢？

我们只需要根据前面提到的的方法，对应相乘就好了。

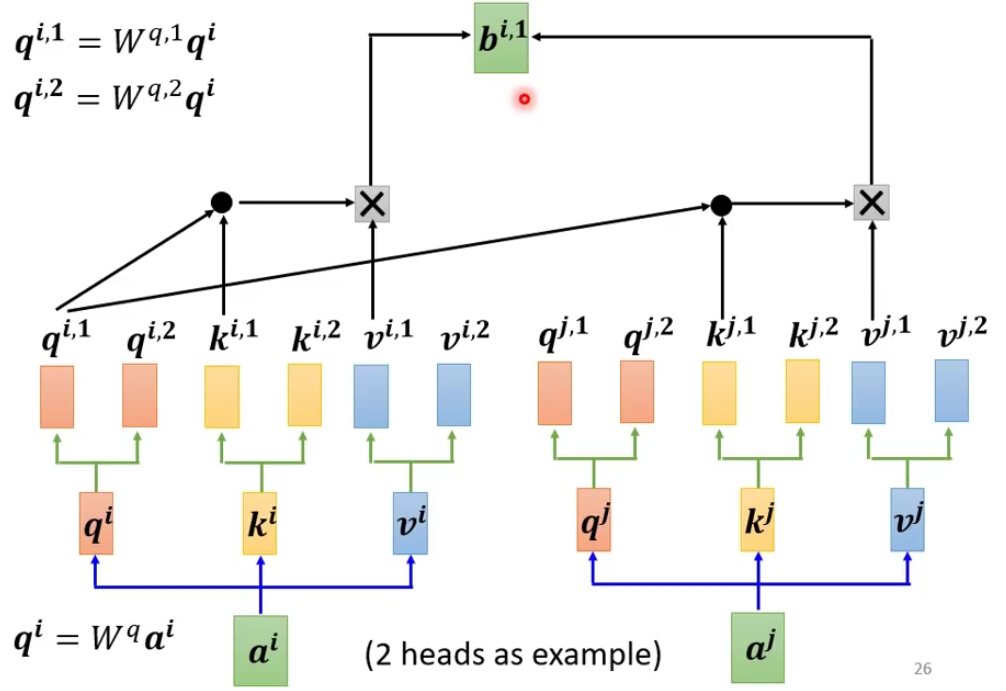
上图中只是一个“头”的计算，那么另一个头的计算方法如下图所示：

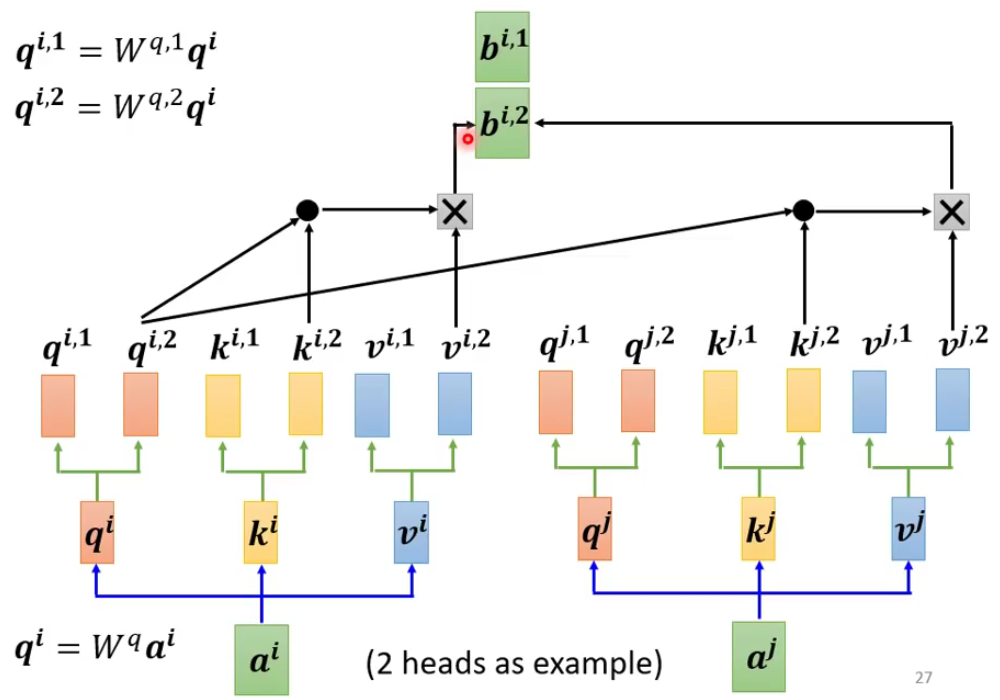
最后只需要将结果合并就好了：

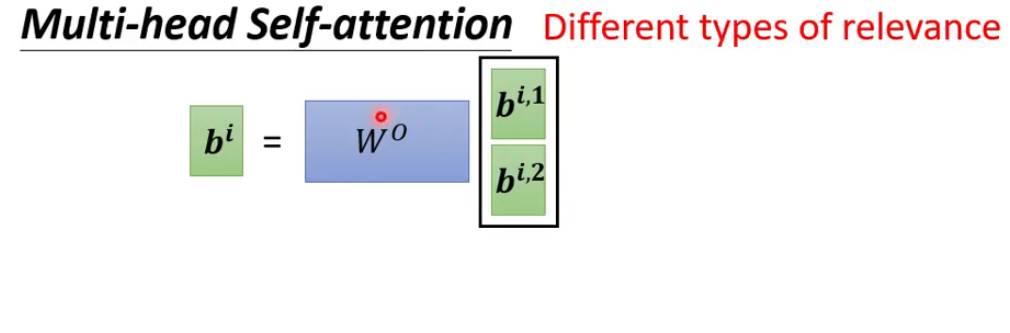
位置编码

我们其实一直没有讨论位置信息，因为位置信息是很重要的，比如在词性标注的时候，句子的一开始一般来说不会是动词，这样就可以帮助我们在一定程度上的决策。

下图就是一个计算位置编码的过程，其中右边是$e^i$向量，每一个column代表一个向量 。

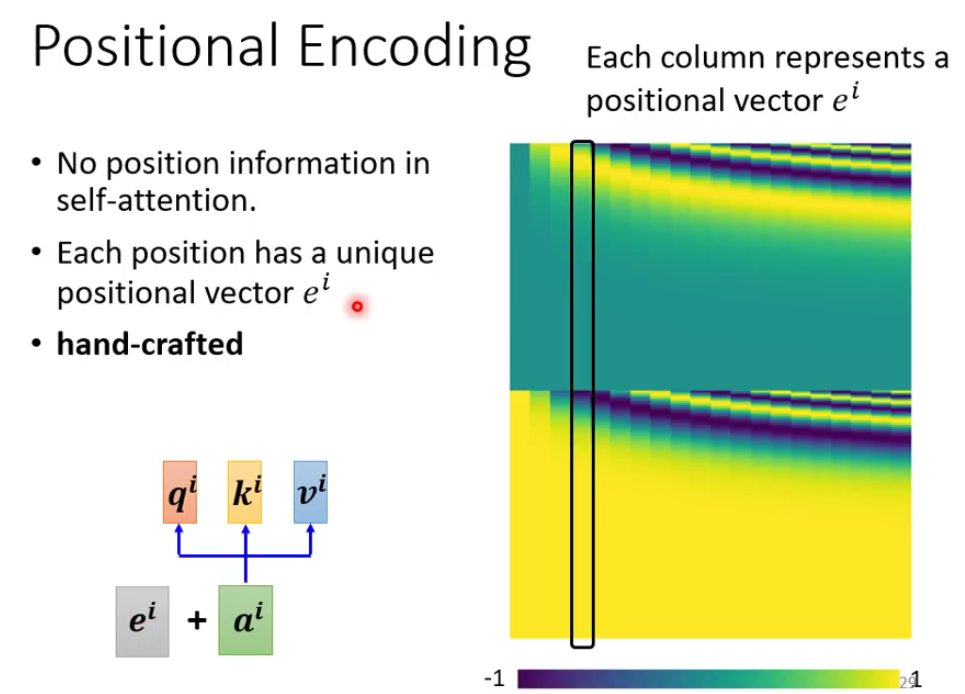
至于这个position 的选择，现在也没有一个定论，如何选择，是手动选择还是从数据中自己学习也尚未确定，下图中是一篇论文中提出的相关讨论：

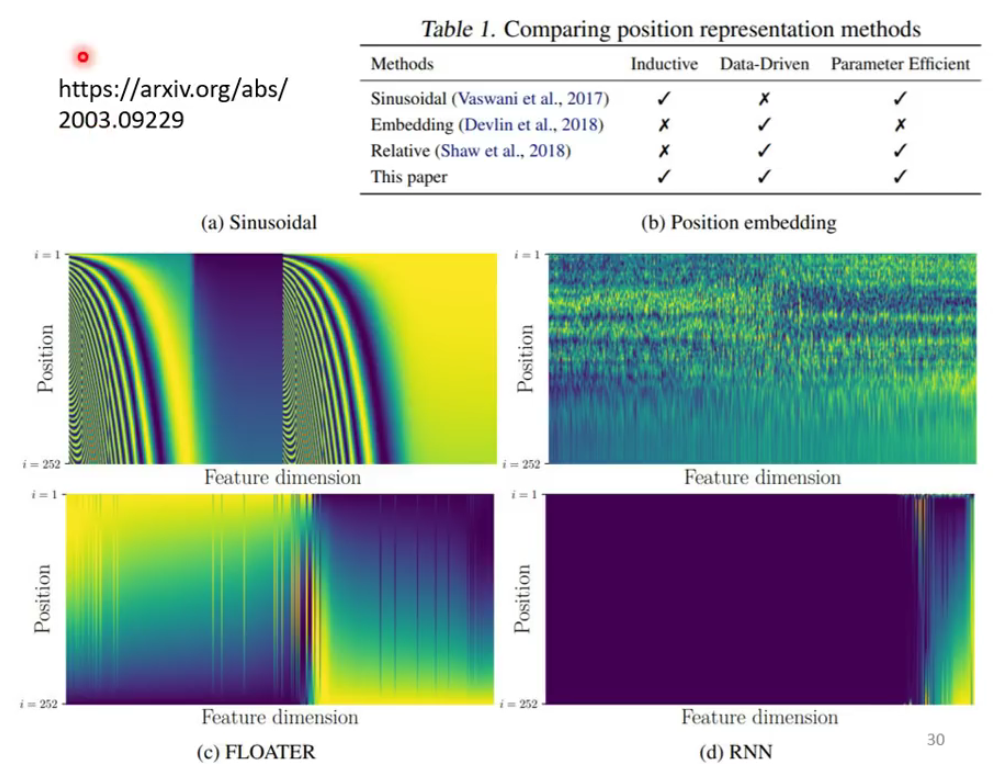
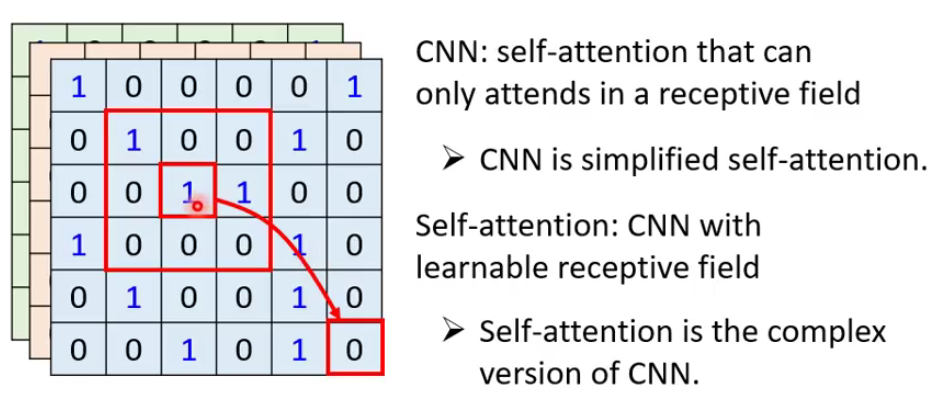
Self-attention v.s. CNN

Self-Attention 在全局中找到相关的pixel，就好像CNN中的窗口(reception field) 是自动学出来的一样。

一下是自监督学习与CNN的区别做了一个简单总结：

• CNN是一种简单的自注意力机制；(CNN只需要考虑人工设定的区域即可)
• 反过来说，自注意力机制是一种复杂的CNN；(自注意力机制则是一种)

关于这两个的关系在一篇名为《On the relationship between self-attention and convolution layers》通过严谨的数学公式来证明了这个过程。

下面这张图片表示了在不同数据集上的效果图，发现，在数据集不大的情况下，CNN的效果是优于self- attention的，反之CNN的效果会差一些。

Self-attention v.s. RNN

下图中简单介绍了RNN和self-attention的机制区别，首先是第一个区别就是，在下图中最后面的黄色的输出值在RNN中很难去考虑第一个的RNN的输入(当然双向的RNN也是可以实现的，或者改进的RNN，如LSTM)，而在self-attention中是很容易去实现的。

下图是说明了另一个问题——RNN不能够实现并行计算，但是Self-attention是可以实现的。

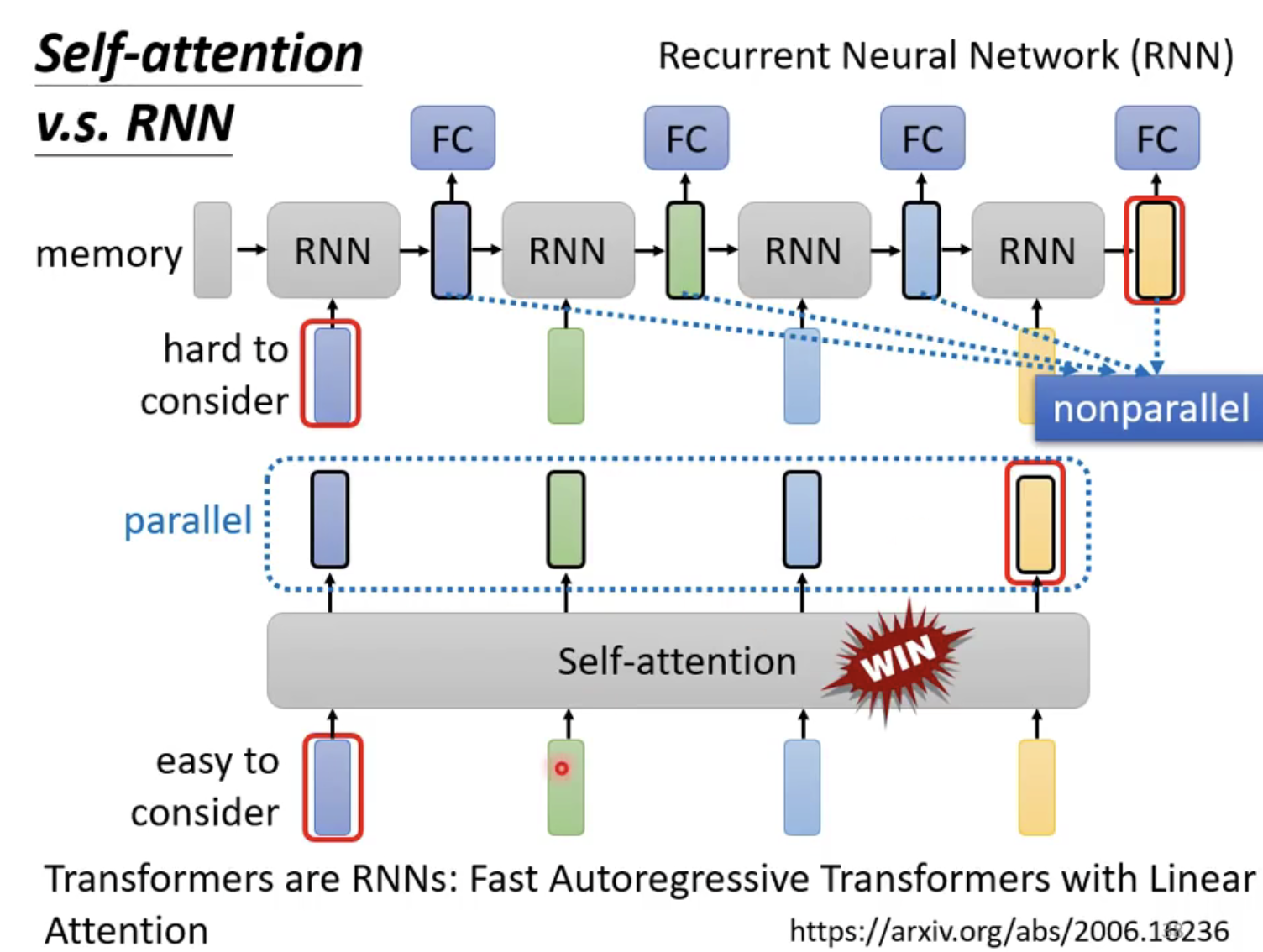
上面这篇文章提到了self-attention加入了什么东西之后，会变成RNN。

进一步研究

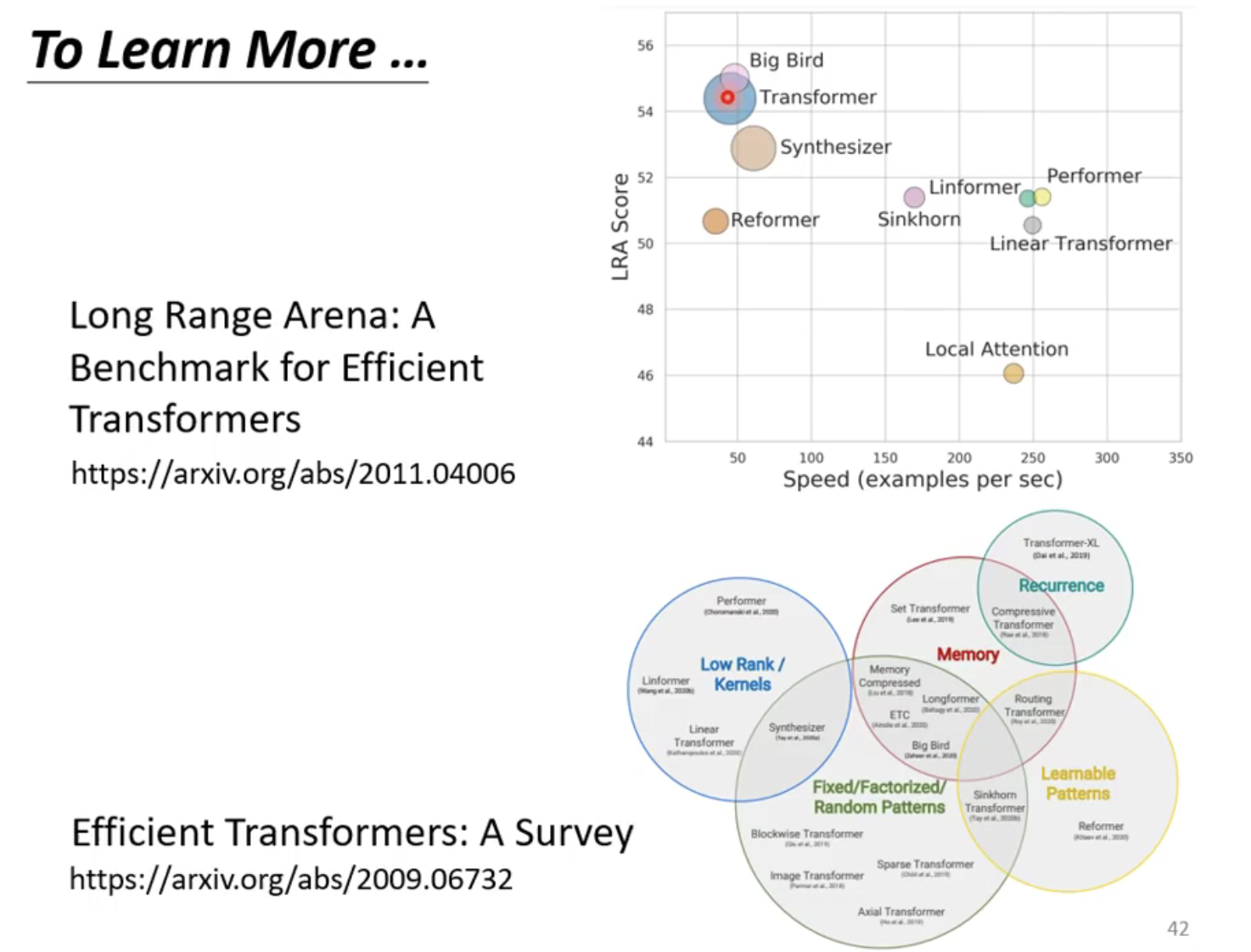
tion是可以实现的。

上面这篇文章提到了self-attention加入了什么东西之后，会变成RNN。

进一步研究

[外链图片转存中…(img-BYvL9z58-1686470533731)]