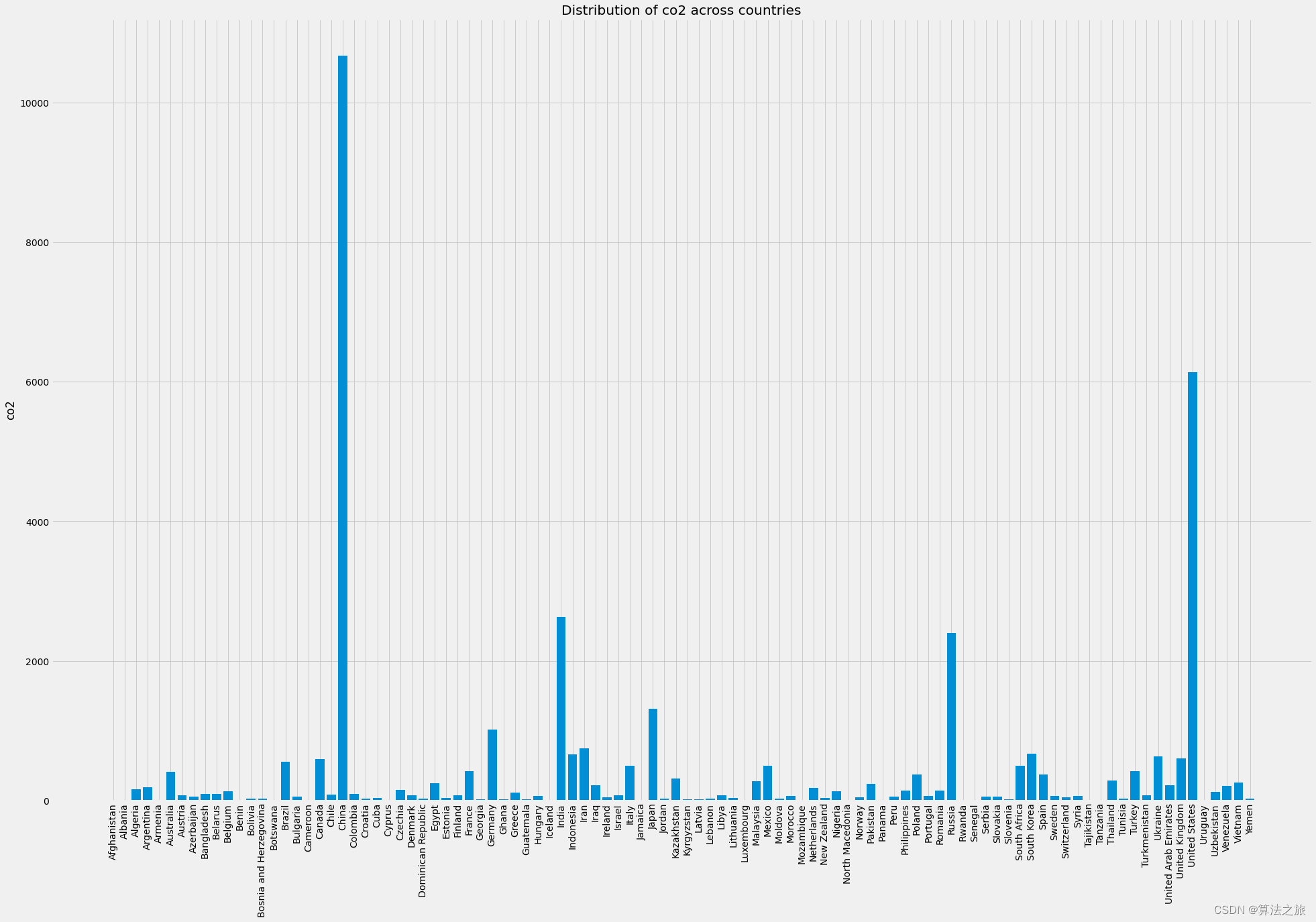
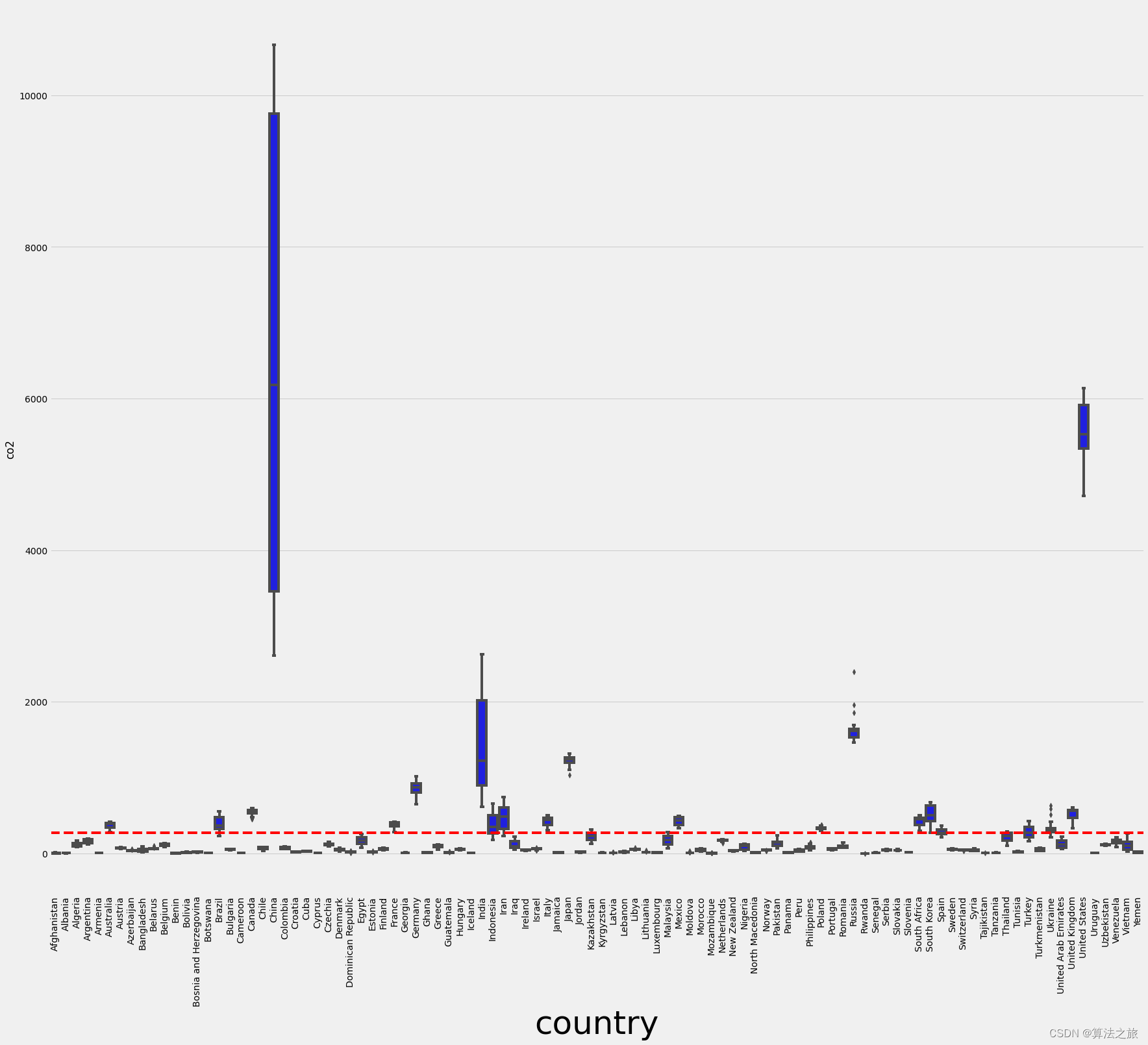
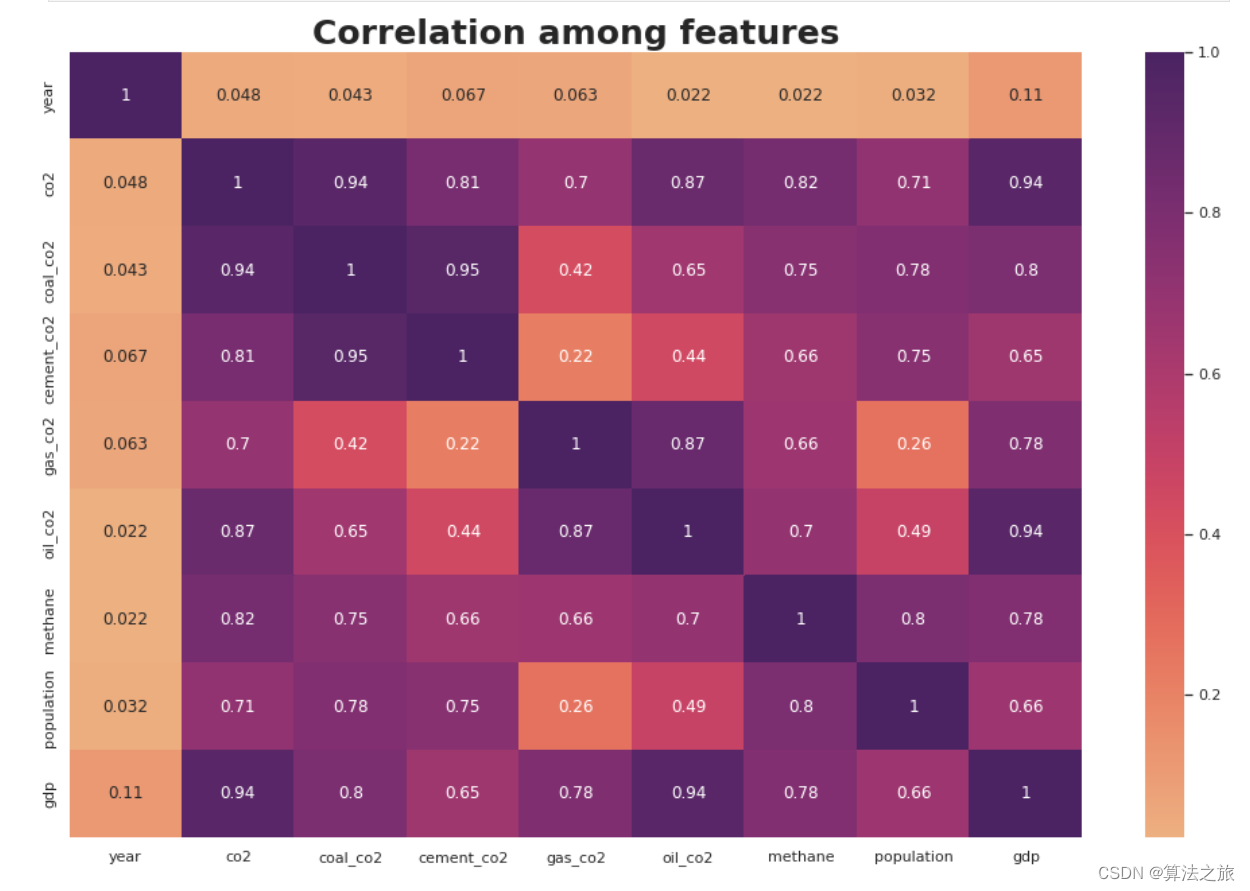
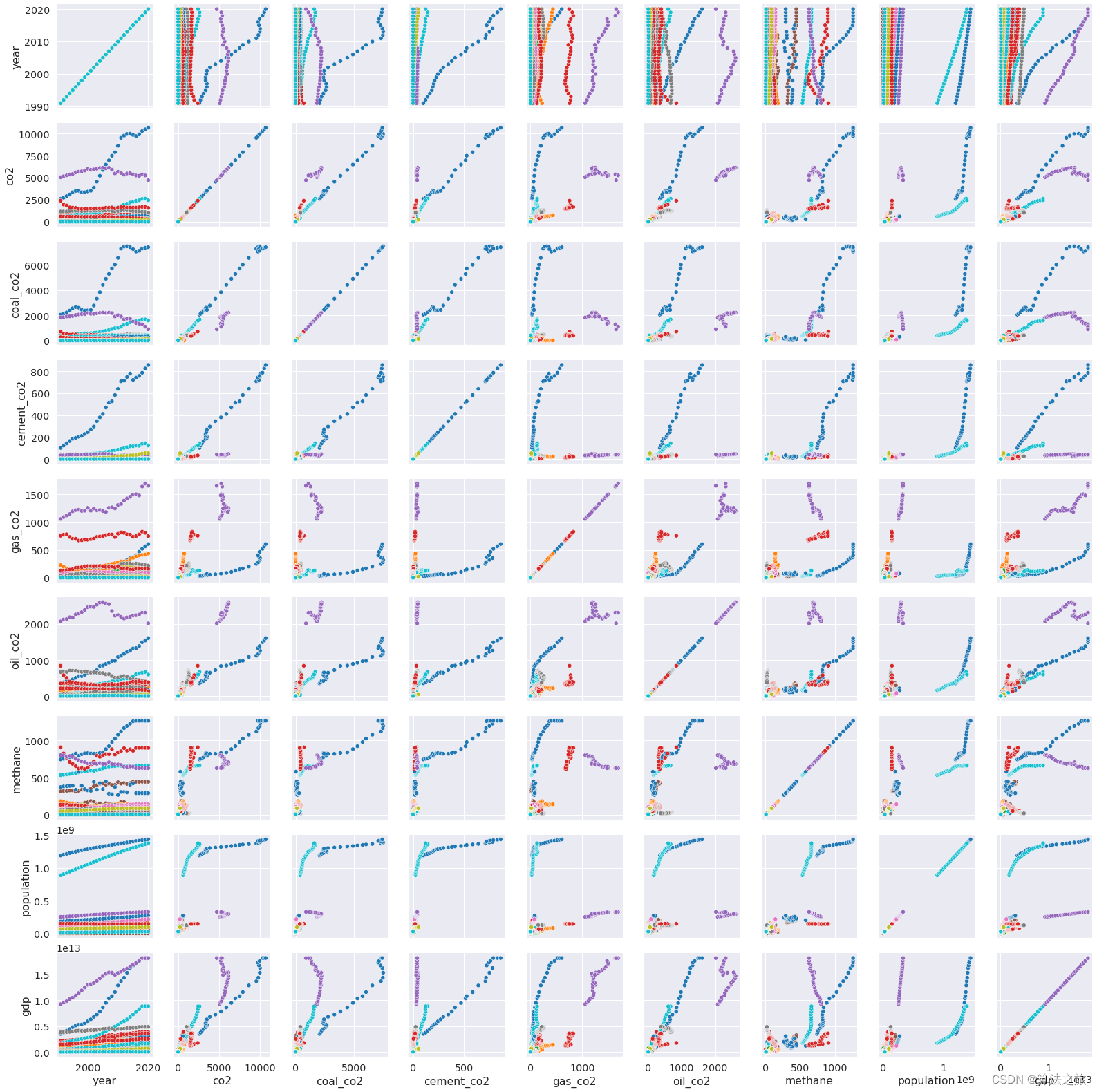
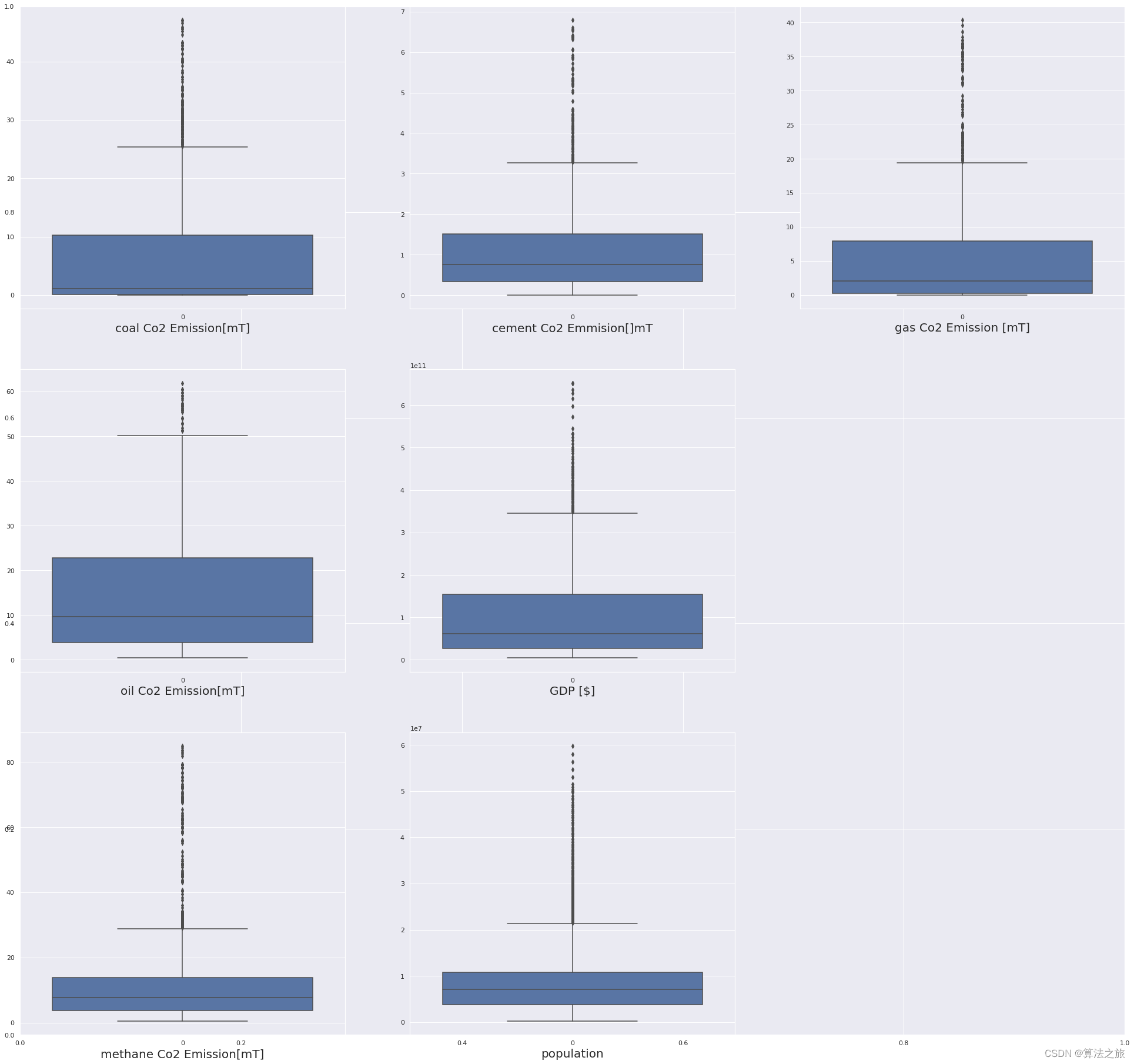
碳排放预测模型 | Python实现基于机器学习回归分析的碳排放预测模型——数据可视化和探索
news2024/11/18 17:47:19
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/633917.html
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！相关文章
Netty实战（十二）
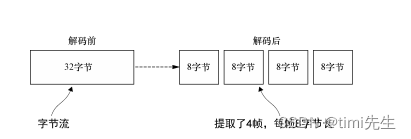
预置的ChannelHandler和编解码器（二）HTTPS、WebSocket的添加使用和大型数据写入以及几种常见的序列化 一、基于Netty的HTTPS程序1.2 使用HTTPS2.3 WebSocket 二、空闲连接和超时三、 解码基于分隔符的协议和基于长度的协议3.1 基于分割符的协议3.2 基于长…
策 略 模 式「指 鼠 为 鸭」
前言
大家好，我是 god23bin，今天我们来介绍下设计模式中的一个重要的设计模式——策略模式。
当涉及到某个行为或算法有多个变体时，策略模式是一种常见的设计模式。它允许在运行时选择使用不同的策略，而无需修改现有代码。
现在…
OneFormer:规则通用图像分割的一个Transformer
文章目录 OneFormer: One Transformer to Rule Universal Image Segmentation摘要本文方法实验结果 OneFormer: One Transformer to Rule Universal Image Segmentation
摘要
通用图像分割并不是一个新概念。过去统一图像分割的尝试包括场景解析、全景分割，以及最…
【工具】SecureCR-8.5下载、安装激活和使用教程（包含常用设置）
目录 一、安装包下载
二、安装教程 三、激活操作
四、使用教程 五、常用设置 一、安装包下载
SecureCRT8.5安装包：
链接：https://pan.baidu.com/s/1yy677I99ln_3evoHc5dMXg 提取码：9tyj
二、安装教程
1. 解压、双击进行安装 2. 安装进…
【LeetCode】136. 只出现一次的数 python
目录 题目描述
第一次刷题
第二次刷题
异或运算的规则 题目描述
给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题，…
![[LeetCode周赛复盘] 第 106 场双周赛20230611](https://img-blog.csdnimg.cn/796d90e5376a490aaaf432e5acd0f166.png)
[LeetCode周赛复盘] 第 106 场双周赛20230611
[LeetCode周赛复盘] 第 106 场双周赛20230611 一、本周周赛总结6461. 判断一个数是否迷人1. 题目描述2. 思路分析3. 代码实现 6425. 找到最长的半重复子字符串1. 题目描述2. 思路分析3. 代码实现 6426. 移动机器人1. 题目描述2. 思路分析3. 代码实现 6463. 找到矩阵中的好子集…
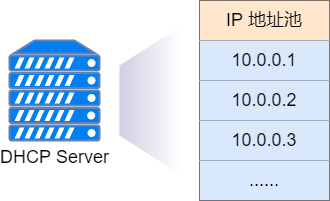
DHCP是什么？它有什么作用？其工作模式？工作原理？
目录 一、DHCP是什么？二、DHCP的作用？1. 在没有DHCP服务的网络中2. 在有DHCP服务的网络中 三、DHCP的工作模式简介四、DHCP的工作原理五、参考资料 一、DHCP是什么？
DHCP是动态主机配置协议（Dynamic Host Configuration Protocol…
![Vue 封装ajax请求[接口]函数](https://img-blog.csdnimg.cn/7614f81d8a20497f806b911e3c450a87.png)
Vue 封装ajax请求[接口]函数
在Vue项目开发当中，当有了后端提供的数据接口之后呢，就需要来为接口定义接口的请求函数，那么在去定义接口函数之前可以先来封装一个ajax请求函数；可能有的初学者在之前的一些篇目当中看到这个vue发起数据请求的不是使用axios的吗&…
3.MySQL表的增删改查（基础）
文章目录 ☕️1. CRUD☕️🍵2. 新增（Create）🍵🍼2.1 单行数据 全列插入🍼🍺2.2 多行数据 指定列插入🍺🍸2.3关于时间的插入格式(homework数据表)：…
串口RS232、RS485最本质区别
由下图可看出不管是RS232还是RS485，其本质都是串口通信，只不过是串口通信电平上的变种而已。所以，我们首先从串口通信讲起。 1、串口通信 任何一种通信都要有物理接口和通信协议。串口通信物理接口如下图： 串口通信协议首先要约…
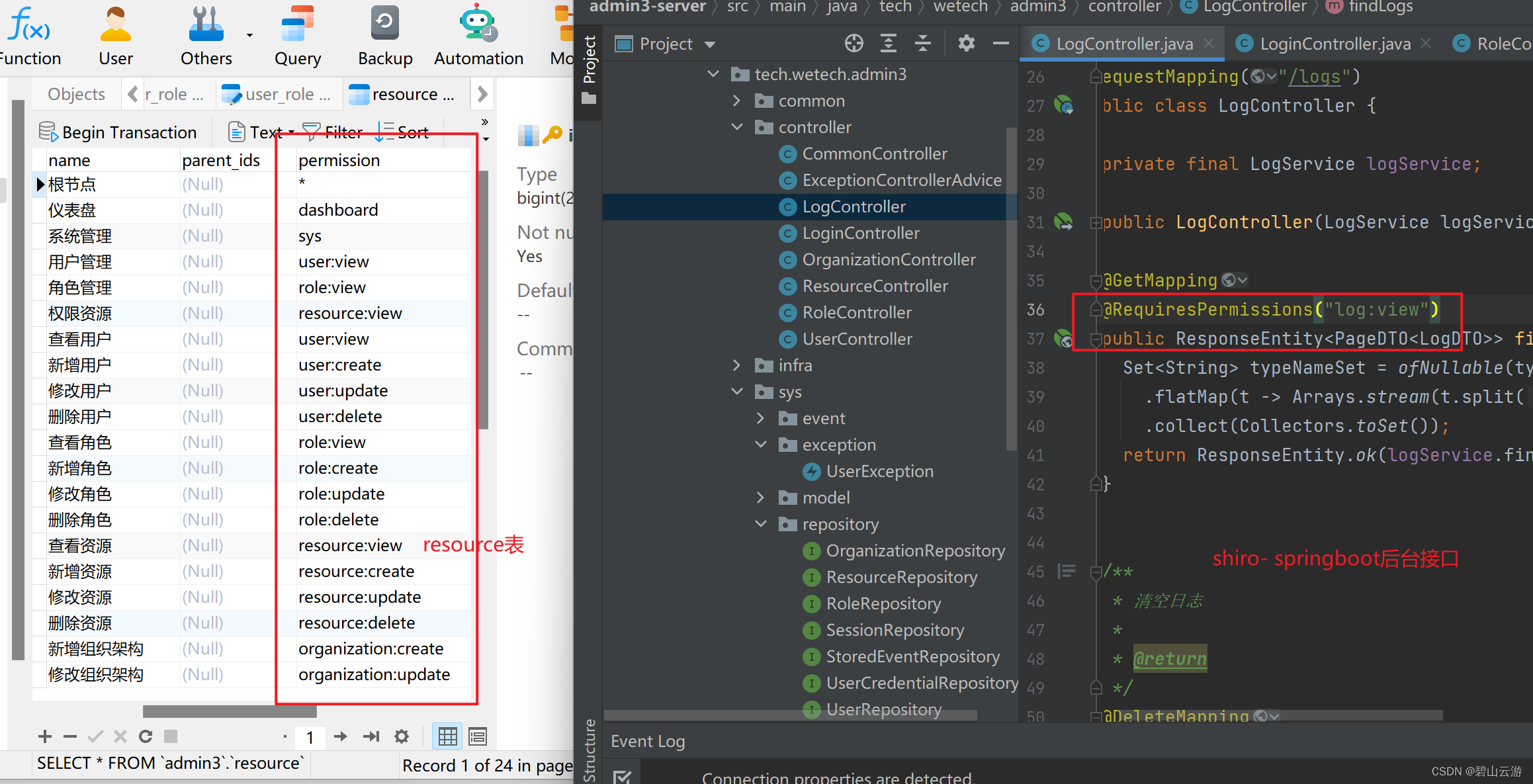
RBAC权限管理，Shiro实践
概念介绍
RBAC是指基于角色的访问控制（Role-Based Access Control），它是一种广泛应用于计算机安全领域的访问控制机制。RBAC通过将用户分配到不同的角色，来控制用户对系统中资源的访问权限。
在RBAC中，每个角色都被…
LVS-DR群集部署
目录
一、LVS-DR数据包流向分析
二、 DR 模式的特点
总结 三、LVS-DR中的ARP问题
1.在局域网中具有相同的IP地址，势必会造成各服务器ARP通信的紊乱
2.路由器根据ARP表项，会将新来的请求报文转发给RealServer，导致Director的VIP失效
3.解…
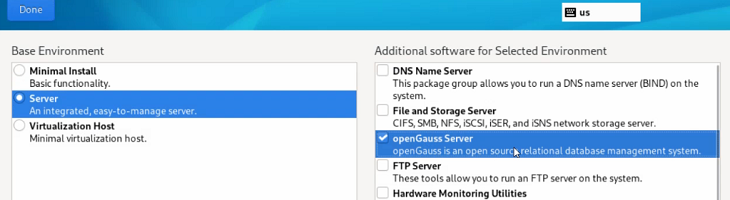
openGauss5 企业版之yum方式安装
文章目录 1. 支持的架构和操作系统版本2. 使用限制3. 安装方式4. 使用说明 本章节主要介绍在openEuler 22.03 LTS操作系统上，通过yum命令一键安装openGauss数据库。 1. 支持的架构和操作系统版本
x86-64 openEuler 22.03 LTSARM64 openEuler 22.03 LTS
仅在openEu…
【博学谷学习记录】超强总结，用心分享 | 架构师 Maven学习总结
文章目录 Maven基本1.什么是Maven2.为什么用Maven?（1）jar 包的规模（2） jar 包的来源（3）jar 包之间的依赖关系 3.Maven目录结构4.maven仓库配置 Pom层次Pom文件简介Super POM 依赖管理1 依赖传递2 传递性依…
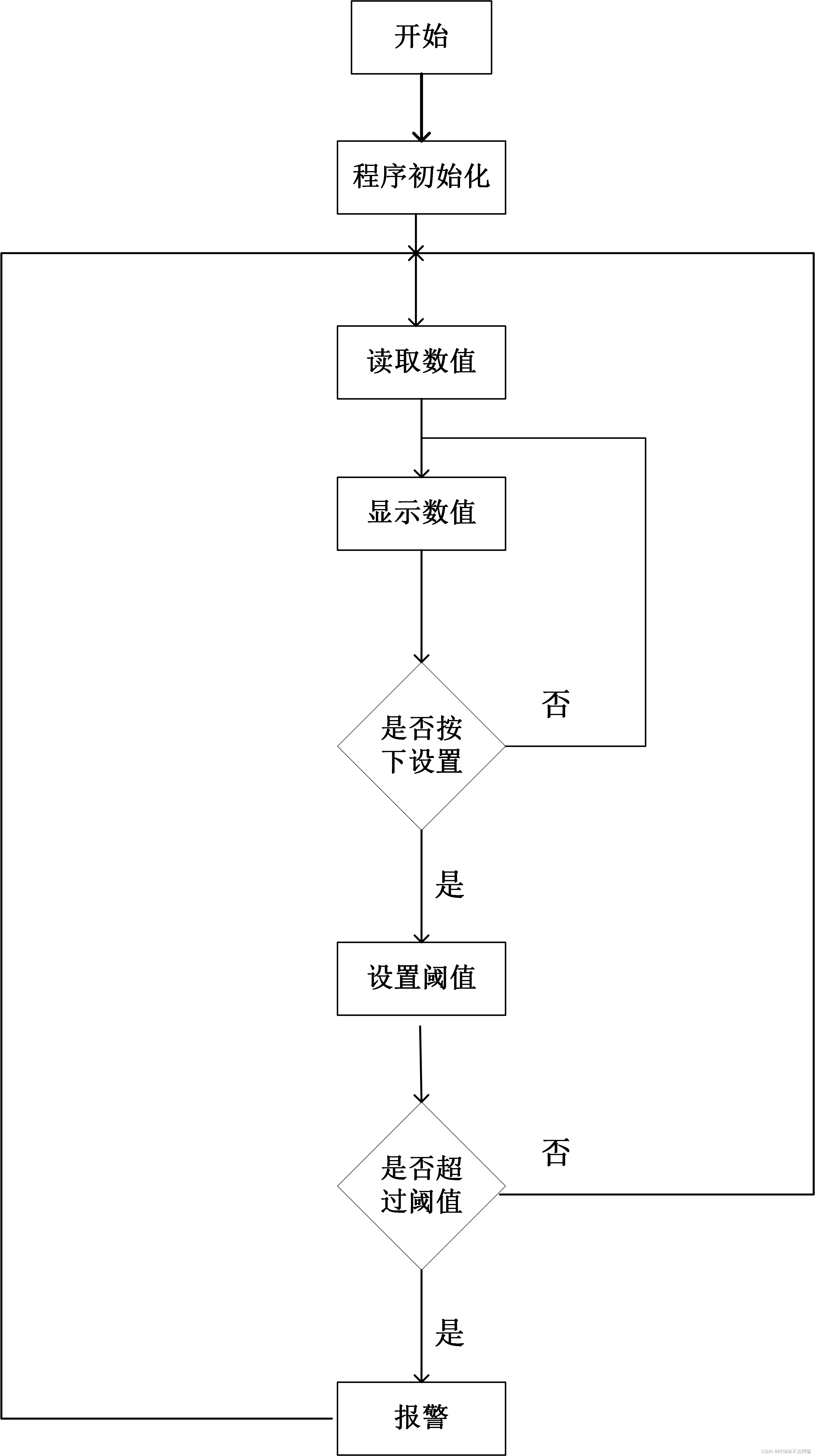
基于51单片机的智能火灾报警系统温度烟雾光
wx供重浩：创享日记 对话框发送：火灾报警 获取完整源码源文件电路图仿真文件论文报告等 功能简介
51单片机MQ-2烟雾传感ADC0832模数转换芯片DS18B20温度传感器数码管显示按键模块声光报警模块
具体功能： 1、实时监测及显示温度值和烟雾浓度…
【Docker】docker部署springboot+vue+mysql+nginx前后端分离项目【部署实战篇】
文章目录 0、安装docker并准备一个springboot-vue前后端分离项目前后端打包放到服务器上1、docker 安装jdk2、docker 安装mysql通过Docker命令进入Mysql容器内部初始化数据sqlDbx连接查看 3、docker build构建后端镜像修改配置数据库JDBC链接IP为虚拟机服务器IPmaven clean pac…
【MySQL】一文带你掌握聚合查询和联合查询
文章目录 1. 聚合函数1.1 COUNT1.2 SUM1.3 AVG1.4 MAX，MIN 2. GROUP BY3. HAVING4. 联合查询4.1 内连接4.2 外连接4.3 自连接4.4 子连接 5.合并查询5.1 UNION5.2 UNION ALL 1. 聚合函数 概念： 聚合函数是一种用于处理数据集合的函数，它将多个…
Fiddler 抓包的八个实用技巧，你学会了吗？
目录 前言
1、双击Session时，使响应页始终显示到”json”tab页；使请求页始终显示到“webform”tab页
2、显示每个Session 的请求IP地址
3、修改响应Header中的Content-Type
4、右键session 直接使用浏览器打开url
5、Session列中，显示每…
电脑拷贝到u盘数据丢失原因分析|3种恢复方法
在电脑操作中，经常需要将数据拷贝到U盘中进行备份或传输。但有时候，我们可能会遇到数据在拷贝或传输过程中丢失的情况。这种情况下，我们该如何找回这些丢失的数据呢？ 下面，为大家介绍一些恢复U盘数据的方法，…
![[ICNN 1993] Optimal brain surgeon and general network pruning](https://img-blog.csdnimg.cn/8002965a019349669a6c4090a342d4ca.png#pic_center)
[ICNN 1993] Optimal brain surgeon and general network pruning
Contents IntroductionMethodOptimal brain surgeon (OBS)Computing the inverse HessianThe ( t − o ) → 0 (\mathbf t-\mathbf o)\rightarrow 0 (t−o)→0 Approximation References Introduction
作者提出 Optimal brain damage (OBD) 的改进 Optimal brain surgeon (OB…