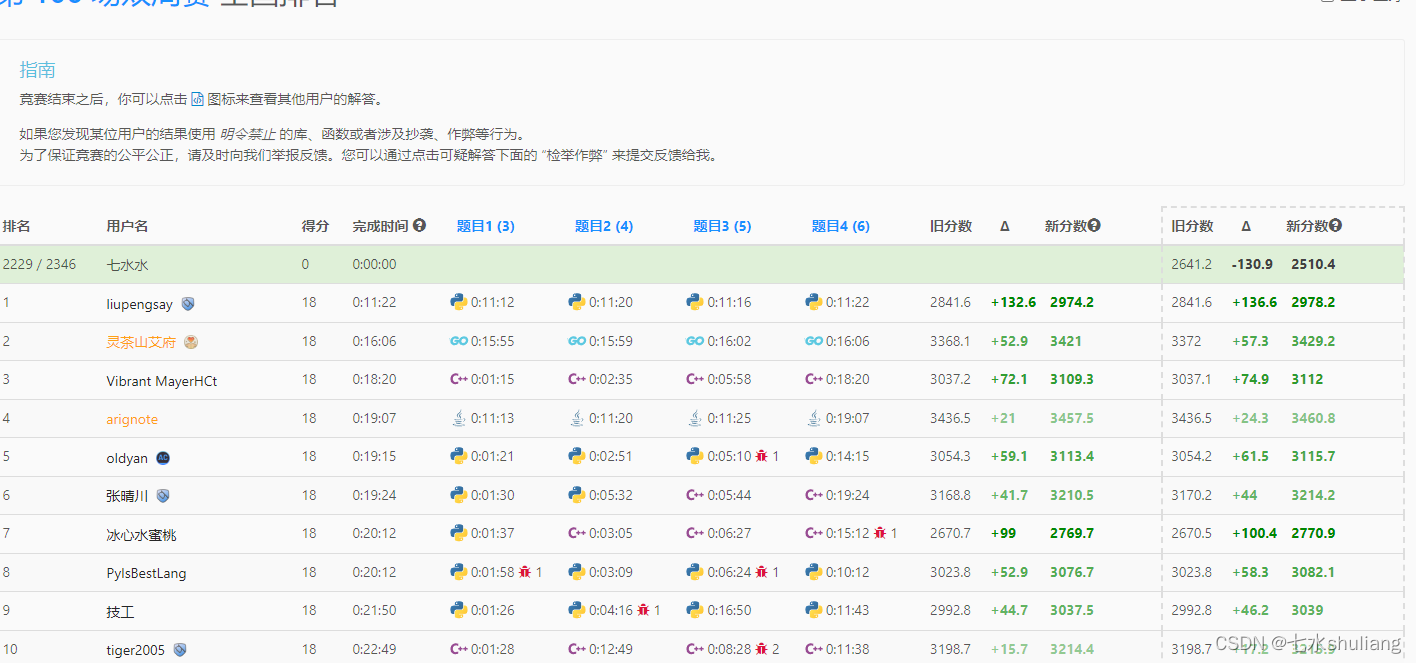
一、本周周赛总结

• T1 模拟。
• T2 滑窗。
• T3 前后缀分解。
• T4 脑筋急转弯+子集型枚举。

6461. 判断一个数是否迷人

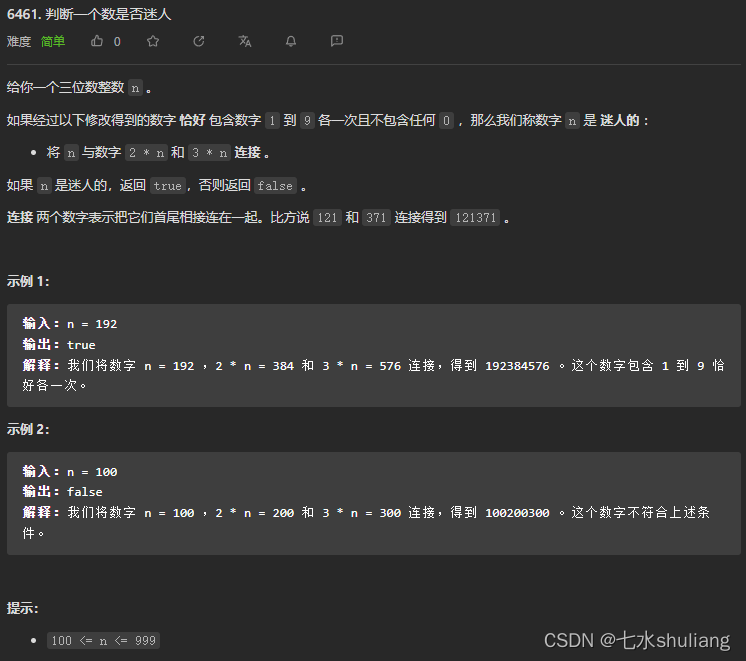
6461. 判断一个数是否迷人

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def isFascinating(self, n: int) -> bool:
        p = str(n) + str(n*2)+str(n*3)
        s = set(p)
        if len(s) == len(p)==9 and '0' not in s:
            return True 
        return False

6425. 找到最长的半重复子字符串

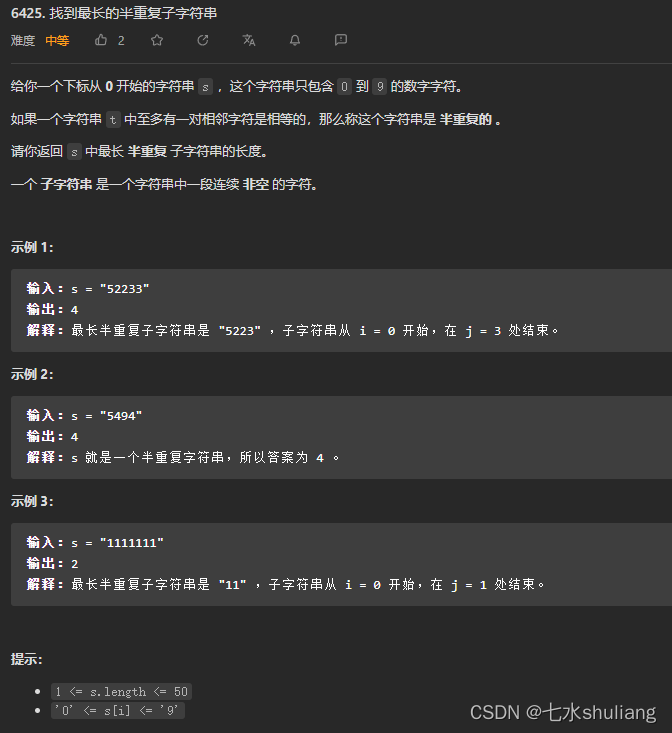
6425. 找到最长的半重复子字符串

1. 题目描述

2. 思路分析

数据量小可以暴力。

• 滑窗，记录窗口内相同邻居的对数，超过1就缩左窗、

3. 代码实现

class Solution:
    def longestSemiRepetitiveSubstring(self, s: str) -> int:
        ans = 1
        q = deque()
        cnt = 0
        for i,v in enumerate(s):
            if q and q[-1]==v:
                cnt += 1
            q.append(v)
            while cnt > 1:
                if q[0] == q[1]:
                    cnt -= 1
                q.popleft()
            ans = max(ans,len(q))
        return ans 

6426. 移动机器人

6426. 移动机器人

1. 题目描述

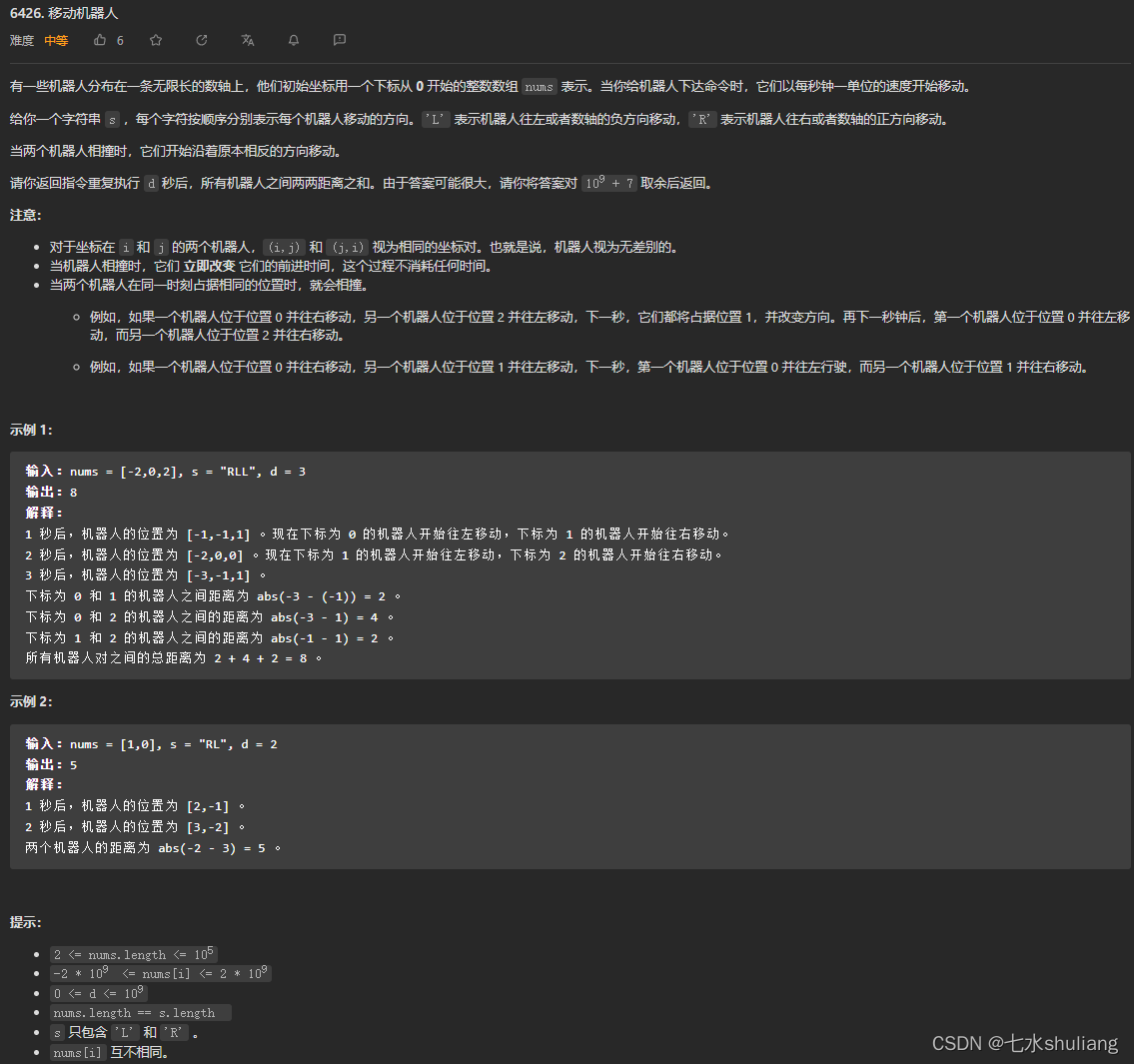
2. 思路分析

• 首先发现机器人是相同不做区分的，那么相撞后反向，和穿过是一样的。注意两个机器人可以在同一位置。
• 那么先暴力计算每个机器人最终位置，然后排序。
• 接下来计算每个机器人到其他所有机器人的位置，前后缀分解即可。
• 最后由于ij和ji不计算两次，答案要除以2。这里取模除以2用费马小定理计算2的逆元。

3. 代码实现

MOD = 10**9+7
class Solution:
    def sumDistance(self, nums: List[int], s: str, d: int) -> int:
        p = []
        for v,c in zip(nums,s):
            if c == 'L':
                p.append(v-d)
            else:
                p.append(v+d)
        p.sort()
        print(p)
        s = sum(p)
        pre = 0
        ans = 0
        n = len(nums)
        for i,v in enumerate(p):
            s -= v 
            ans += v*i-pre + s - v*(n-i-1)
            ans %= MOD
            pre += v             
        
        return ans*pow(2,MOD-2,MOD) % MOD 

6463. 找到矩阵中的好子集

6463. 找到矩阵中的好子集

1. 题目描述

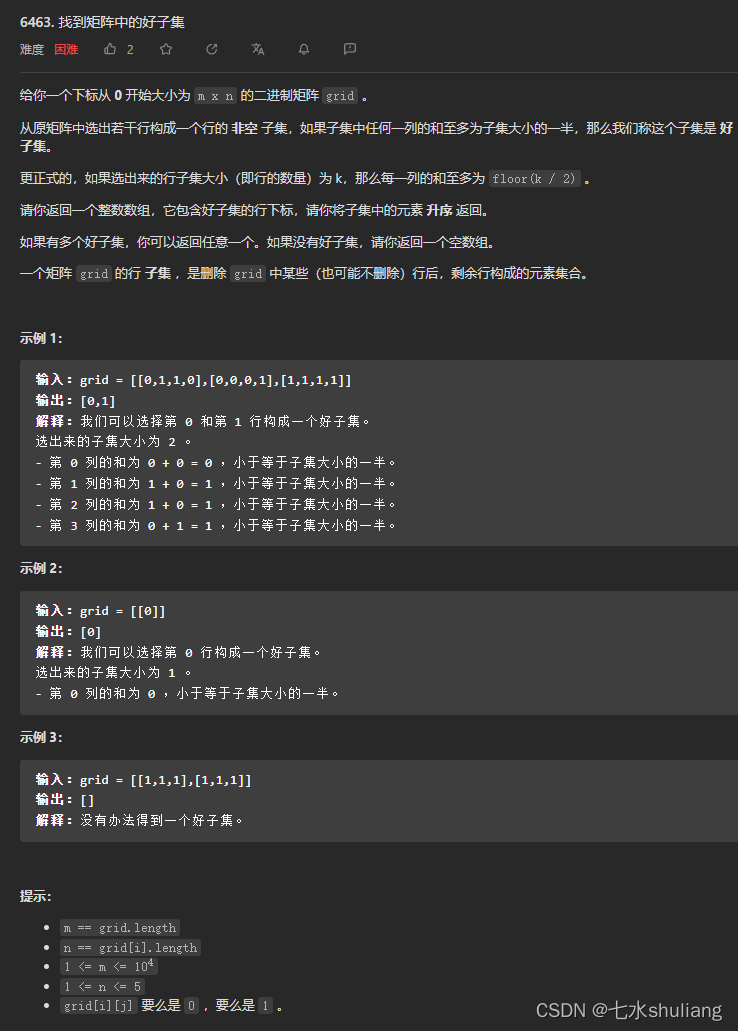
2. 思路分析

• 答案要么1行，要么2行。
• 因此先状压，找全0的行，有就返回它。
• 否则枚举每种状态，找到相反的行，或者相反行的子集，返回他们。
• 找不到就返回空

3. 代码实现

class Solution:
    def goodSubsetofBinaryMatrix(self, grid: List[List[int]]) -> List[int]:
        m, n = len(grid), len(grid[0])
        idx = [[] for _ in range(1 << n)]
        for i, row in enumerate(grid):
            s = 0
            for v in row:
                s = s * 2 + v
            idx[s].append(i)

        if idx[0]:
            return [idx[0][0]]
        mask = (1 << n) - 1
        for i, vs in enumerate(idx):
            if not vs:
                continue
            v = vs[0]
            j = i^mask
            p = j
            while p:
                if idx[p]:
                    return sorted([v,idx[p][0]])
                p = j & (p-1)
        # for i, vs in enumerate(idx):
        #     if not vs:
        #         continue
        #     v = vs[0]
        #     for j in range(i+1,1<<n):
        #         if idx[j] and (i&j) == 0:
        #             return sorted([idx[j][0],v])

        return []      

参考链接