融合黄金正弦和随机游走的哈里斯鹰优化算法(GSHHO)
文章目录
- 融合黄金正弦和随机游走的哈里斯鹰优化算法(GSHHO)
- 1.哈里斯鹰优化算法
- 2.改进哈里斯鹰优化算法
- 2.1 黄金正弦算法
- 2.2 非线性能量指数递减策略
- 2.3 高斯随机游走策略
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.python代码
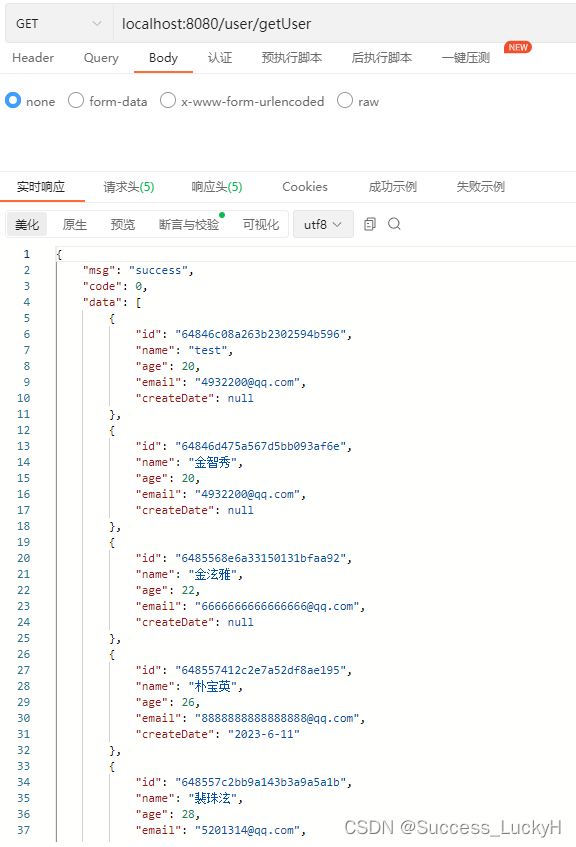
摘要: 针对哈里斯鹰优化算法收敛精度低、易陷入局部最优的问题,本文提出了融合黄金正弦和随机游走的哈里斯鹰优化算法。首先,该算法在哈里斯鹰的探索阶段融合黄金正弦优化算法,增强算法的全局探索能力;其次,使用一种非线性能量指数递减策略,平衡算法的全局探索和局部开发能力;然后,在哈里斯鹰的开发阶段引入高斯随机游走策略对猎物进行随机游走,提升算法的局部开发能力;
1.哈里斯鹰优化算法
基础哈里斯鹰优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/108528147
2.改进哈里斯鹰优化算法
2.1 黄金正弦算法
观察哈里斯鹰优化算法探索阶段的更新公式 (1) 可知原算法在
q
⩾
0.5
q \geqslant 0.5
q⩾0.5 时的搜索过于随机, 也末 能与种群中的其它个体进行交流, 导致算法的全局 搜索能力变差, 难以有效遍历整个解空间。因此, 本 文将黄金正弦优化算法融合到 HHO 的探索阶段, 改进后的探索公式如式(17) 所示:
X
(
t
+
1
)
=
{
X
i
t
∗
∣
sin
(
R
1
)
∣
+
R
2
∗
sin
(
R
1
)
∗
∣
x
1
∗
P
i
t
−
x
2
∗
X
i
t
∣
,
q
⩾
0.5
(
X
rabbii
(
t
)
−
X
m
(
t
)
)
−
r
3
(
L
B
+
r
4
(
U
B
−
L
B
)
)
,
q
<
0.5
(17)
\begin{aligned} & X(t+1)= \\ & \left\{\begin{array}{l} X_i^t *\left|\sin \left(R_1\right)\right|+R_2 * \sin \left(R_1\right) *\left|x_1 * P_i^t-x_2 * X_i^t\right|, q \geqslant 0.5 \\ \left(X_{\text {rabbii }}(t)-X_m(t)\right)-r_3\left(L B+r_4(U B-L B)\right), \quad q<0.5 \end{array}\right. \\ & \end{aligned}\tag{17}
X(t+1)={Xit∗∣sin(R1)∣+R2∗sin(R1)∗∣x1∗Pit−x2∗Xit∣,q⩾0.5(Xrabbii (t)−Xm(t))−r3(LB+r4(UB−LB)),q<0.5(17)
2.2 非线性能量指数递减策略
在 H H O \mathrm{HHO} HHO 算法中, 猎物能量 E E E 的大小起着调节 和过渡全局搜索和局部开采的重要作用, E E E 越小, H H O \mathrm{HHO} HHO 算法越倾向于执行局部开采; E E E 越大, 算法越 倾向于进行全局探索. 但在传统 H H O \mathrm{HHO} HHO 算法的能量 方程中, E E E 由最大值到最小值呈线性递减, 并不能有 效描述自然界中哈里斯噟群体围捕猎物的真实过 程. 数学家模拟捕食者一猎物的相互作用 [ 8 ] { }^{[8]} [8], 得出这 样的结论:随机收缩指数函数更适合于表达猎物逃 跑时的能量变化. 因此, 论文提出修正能量线性递减 调控机制, 将随机收缩指数函数融入猎物能量 E \mathrm{E} E 的 递减过程, 其对应的能量方程为:
在
H
H
O
\mathrm{HHO}
HHO 中,逃逸能量
E
E
E 不仅控制着全局探索 和局部开发的的转换, 而且还决定着哈里斯鹰四种 开发策略的选择。文献 [4]已经指出了原始算法逃 逸能量
E
E
E 后期恒小于 1 , 缺少全局探索,易使算法陷 人局部最优。而文献
[
6
]
[6]
[6] 通过实验指出了指数递减 策略为逃逸能量的最佳策略。因此本文定义了一种 非线性能量指数递减策略, 具体见式( 18)、式(19) :
E
=
2
e
−
(
α
×
t
T
)
+
δ
(18)
\begin{gathered} E=2 e^{-\left(\alpha \times \frac{t}{T}\right)}+\delta \end{gathered}\tag{18}
E=2e−(α×Tt)+δ(18)
δ
=
randn
×
(
sin
β
(
π
2
×
t
T
)
+
cos
(
π
2
×
t
T
)
−
1
)
(19)
\begin{gathered} \delta=\operatorname{randn} \times\left(\sin ^\beta\left(\frac{\pi}{2} \times \frac{t}{T}\right)+\cos \left(\frac{\pi}{2} \times \frac{t}{T}\right)-1\right) \end{gathered}\tag{19}
δ=randn×(sinβ(2π×Tt)+cos(2π×Tt)−1)(19)
其中,
randn
\operatorname{randn}
randn 为
(
0
,
1
)
(0,1)
(0,1) 内的随机数;
α
\alpha
α 的值为
1.3
;
β
1.3 ; \beta
1.3;β 的值为 1.7 。
2.3 高斯随机游走策略
高斯随机游走作为一种经典的随机游走模型, 模型的开发能力比较强。在
H
H
O
\mathrm{HHO}
HHO 的开发阶段引人 高斯随机游走策略, 对种群的最优个体施加扰动, 生 成新的个体, 既利于增强算法的收玫速度, 又可在算 法陷人局部最优时帮助算法跳出局部最优。具体的 高斯随机游走策略见式(20)、式(21):
X
(
t
+
1
)
=
Gussian
(
X
rabbit
t
,
τ
)
(20)
X(t+1)=\operatorname{Gussian}\left(X_{\text {rabbit }}^t, \tau\right) \tag{20}
X(t+1)=Gussian(Xrabbit t,τ)(20)
τ
=
cos
(
(
π
2
∗
t
T
)
2
)
×
(
X
rabbit
t
−
X
rand
(
t
)
)
(21)
\begin{gathered} \tau=\cos \left(\left(\frac{\pi}{2} * \frac{t}{T}\right)^2\right) \times\left(X_{\text {rabbit }}^t-X_{\text {rand }}(t)\right) \end{gathered}\tag{21}
τ=cos((2π∗Tt)2)×(Xrabbit t−Xrand (t))(21)
其中,
X
r
a
b
b
i
t
t
X_{r a b b i t}^t
Xrabbitt 为第
t
t
t 次迭代中猎物的位置, 即最优 个体的位置。
3.实验结果

4.参考文献
[1]聂春芳.融合黄金正弦和随机游走的哈里斯鹰优化算法[J].智能计算机与应用,2021,11(07):113-119+123.