北邮22信通：第六章查找：BST树表（代码超详细逐步图解）

news2024/11/24 4:26:31

北邮22信通一枚~   

跟随课程进度每周更新数据结构与算法的代码和文章 

持续关注作者  解锁更多邮苑信通专属代码~

获取更多文章  请访问专栏：

北邮22信通_青山如墨雨如画的博客-CSDN博客

目录

讲解

1.构造函数

2.析构函数

 3.查询函数

4.删除操作 （重点）

第一种情况：

第二种情况：

第三种情况：

结合实例详解第三种情况

1.删除30：

 2.删除20：

代码部分

效果图：

 代码：

运行结果：

讲解

1.构造函数

BST树表的一大特点，就是任取一个节点，其左子树中任意一个节点的权值都小于这个结点，右子树中任意一个节点的权值都大于这个节点。根据这种特性，要想实现构造函数的书写，我们就必须考虑这样一个问题：每给出一个权值，我们要将这个权值插入到树表的哪个位置上。

所以首先讲解insert_bst函数：

insert函数传入两个参数，一个是访问的初始位置，用指针指示；另一个参数是待插入的节点。

首先，如果这个树表是空的，那么直接将这个待插入的节点作为根节点插入。

其次，如果树表不是空的，那么就会有两种情况：待插入的节点的权值大于或者小于当前访问节点的权值。应用递归思想，如果大于，调用insert_bst，传入当前位置所在节点的右孩子节点和待插入节点；如果小于，调用insert_bst，传入当前位置所在节点的左孩子节点和待插入节点。

代码部分：

template<class temp>
void BST<temp>::insert_bst(binnode<temp>*& r, binnode<temp>* s)
{
	if (r == NULL)
		r = s;
	else if (s->data < r->data)
		insert_bst(r->leftchild, s);
	else
		insert_bst(r->rightchild, s);
}

通过这样的插入方式，就可以让二叉树成为一颗有顺序的BST树。

insert函数实现之后，构造函数的实现显而易见。

每传入一个数据，新建一个节点，开辟一个堆区空间，为新节点赋值，调用insert函数将赋值过后的节点直接插入到BST树中，从而实现了BST树的构造。

2.析构函数

析构函数的实现方法和二叉树析构函数的实现方法相同，核心思路是递归函数，这里不做赘述。

代码部分：

template<class temp>
void BST<temp>::release(binnode<temp>* r)
{
	if (r != NULL)
	{
		release(r->leftchild);
		release(r->rightchild);
		delete r;
	}
}
template<class temp>
BST<temp>::~BST()
{
	release(this->root);
}

 3.查询函数

查询函数也是应用递归思想和BST树的特性。根据BST左子树任一结点小于当前节点右子树任一节点大于当前节点的特性，传入两个参数，一个是开始访问的位置，一个是待查询的数据。

如果当前位置不存在，返回空指针；

如果当前位置的权值正好等于待查询数据，返回指向这个位置的指针；

如果数据小于访问位置的权值，递归调用本函数，查询访问位置的左子树；

如果查询数据大于访问位置的权值，递归调用本函数，查询访问位置的右子树。

代码部分：

template<class temp>
binnode<temp>* BST<temp>::search
(binnode<temp>*& r, temp k)
{
	if (r == NULL)
		return NULL;
	if (k == r->data)
		return r;
	else if (k < r->data)
		return search(r->leftchild, k);
	else
		return search(r->rightchild, k);
}

4.删除操作 （重点）

核心算法是删除关键字所在节点。

在一颗有顺序的二叉树中删除一个结点，确实不容易实现。我们不仅要考虑如何删除节点，还需哟考虑删除节点之后，这个节点的子树怎么重新连接回原来的BST树中。

删除一个节点，无非有3种情况，从易到难依次是：

删除的节点是叶子结点；

删除的节点只有左子树或只有右子树；

删除的节点左右子树都存在。

第一种情况：

直接删除即可；

第二种情况：

删除的节点只有左子树或者只有右子树：

现在设要删除的节点是小明。小明只有左孩子们或只有右孩子们。

如果小明是他爸爸的左孩子，那么小明的孩子们都比小明爸爸的权值小，那么删除小明之后，小明的孩子们都接在小明爸爸的左孩子位置上；如果小明是爸爸的右孩子，那么小明的孩子们都比小明爸爸的权值大，那么删除小明之后，小明的孩子们都接在小明爸爸的右孩子位置上。

第三种情况：

第三种情况也是最复杂的一种情况：如果待删除的节点既有左孩子又有右孩子：

旧帝驾崩需要从王室中选出一个符合条件的世子继承王位。旧帝留下两个分支，左边是等待继位的世子们，右边是朝廷重臣。挑选的世子必须是嫡长子，也就是比所有待继位的世子年龄大，同时要比群臣年龄小。

找到之后，新帝登基，原先所在御殿拆除。

代码部分：

template<class temp>
void BST<temp>::delete_node(binnode<temp>*& r)
{
	binnode<temp>* q, * s;
	if (r->leftchild == NULL)
	{
		q = r;
		r = r->rightchild;
		delete q;
	}
	else if (r->rightchild == NULL)
	{
		q = r;
		r = r->leftchild;
		delete q;
	}
	else
	{
		q = r;
		s = r->leftchild;
		while (s->rightchild != NULL)
		{
			q = s;
			s = s->rightchild;
		}
		r->data = s->data;
		if (q != r)
			q->rightchild = s->leftchild;
		else
			r->leftchild = s->leftchild;
		delete s;
	}
}

结合实例详解第三种情况

BST树：

                                                                                 

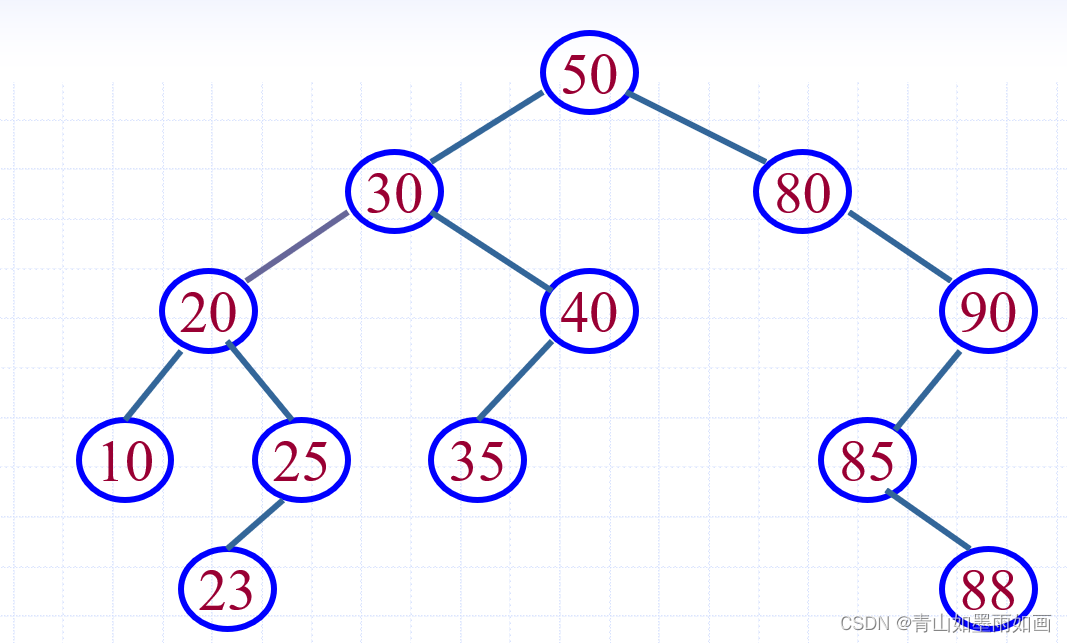
1.删除30：

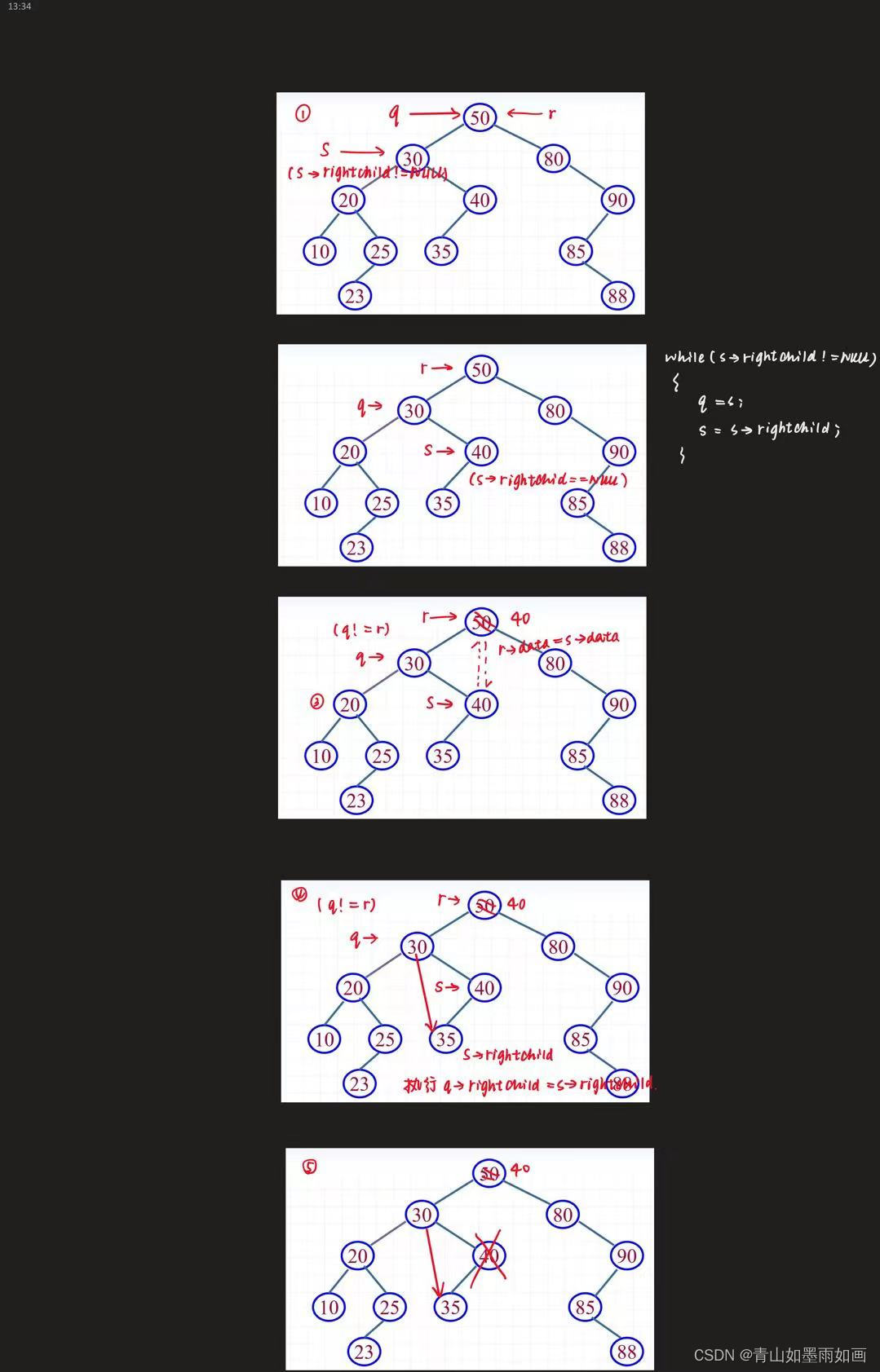
 2.删除20：

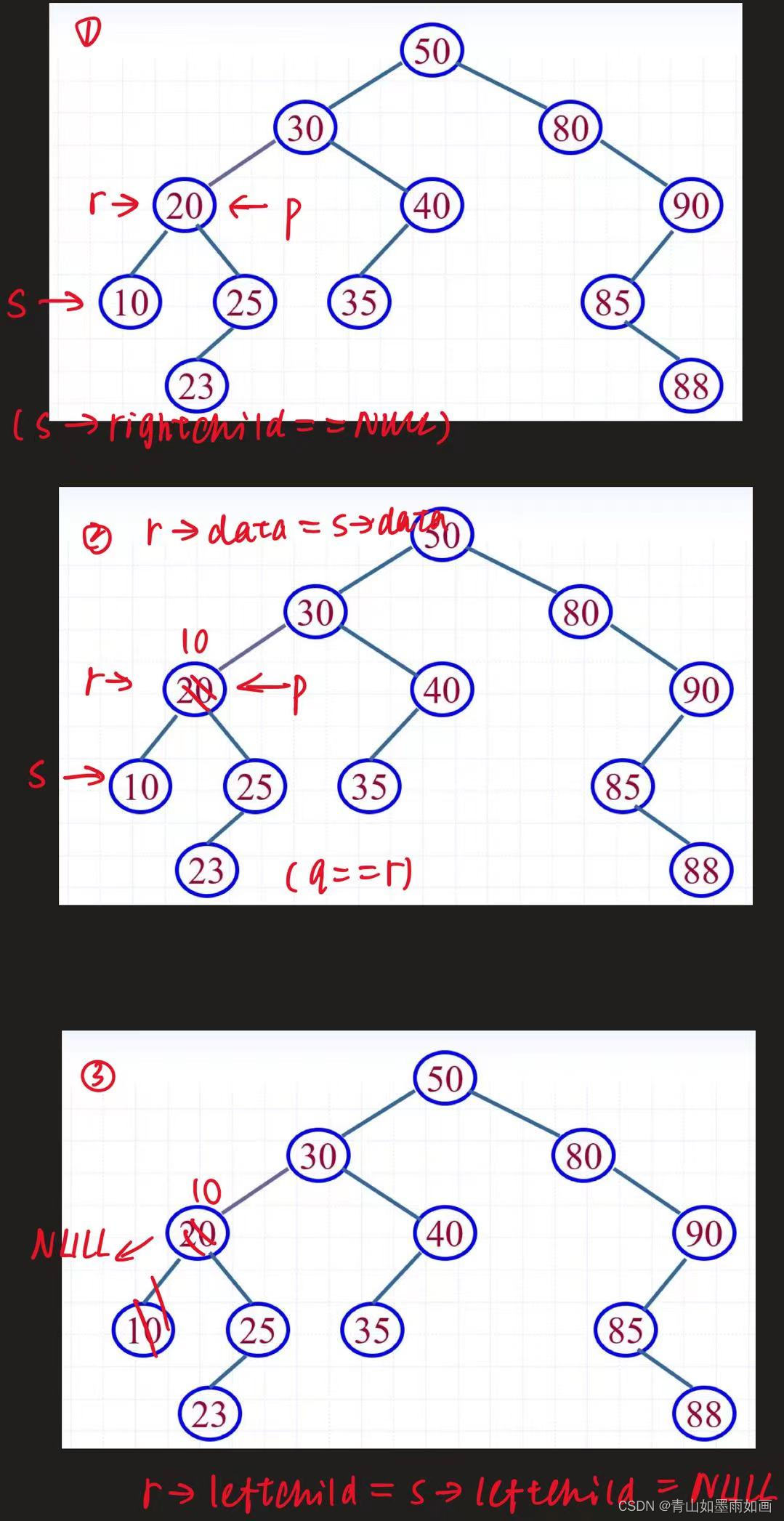
删除操作总体代码：

template<class temp>
bool BST<temp>::delete_key(binnode<temp>*&r,temp k)
{
	if (r == NULL)
		return false;
	else
	{
		if (k == r->data)
		{
			delete_node(r);
			return true;
		}
		else if (k < r->data)
			return delete_key(r->leftchild, k);
		else
			return delete_key(r->rightchild, k);

	}
}
template<class temp>
void BST<temp>::delete_node(binnode<temp>*& r)
{
	binnode<temp>* q, * s;
	if (r->leftchild == NULL)
	{
		q = r;
		r = r->rightchild;
		delete q;
	}
	else if (r->rightchild == NULL)
	{
		q = r;
		r = r->leftchild;
		delete q;
	}
	else
	{
		q = r;
		s = r->leftchild;
		while (s->rightchild != NULL)
		{
			q = s;
			s = s->rightchild;
		}
		r->data = s->data;
		if (q != r)
			q->rightchild = s->leftchild;
		else
			r->leftchild = s->leftchild;
		delete s;
	}
}

代码部分

效果图：

 代码：

#include<iostream>
using namespace std;
class student
{
private:
	int ID;
	string name;
public:
	int existence;
	student()
	{
		this->ID = 0;
		this->name = "unknown name";
		this->existence = 0;
	}
	student(int ID, string name)
	{
		this->ID = ID;
		this->name = name;
		this->existence = 1;
	}
	friend ostream& operator<<(ostream& output, student& s)
	{
		output << s.ID << " " << s.name << endl;
		return output;
	}
	void print()
	{
		cout << this->name << " " << this->ID << endl;
	}
	bool operator <(student& s)
	{
		return (this->ID < s.ID) ? true : false;
	}
	bool operator>(student& s)
	{
		return (this->ID > s.ID) ? true : false;
	}
	bool operator==(student& s)
	{
		return (this->ID == s.ID) 
			&& (this->name == s.name) ? true : false;
	}
	bool operator !=(student& s)
	{
		return (this->ID != s.ID)
			|| (this->name != s.name) ? true : false;
	}
};

template<class temp>
struct binnode
{
	temp data;
	binnode<temp>* leftchild;
	binnode<temp>* rightchild;
};

template<class temp>
class BST
{
public:
	BST(temp r[], int n);
	void insert_bst(binnode<temp>*& r, binnode<temp>* s);
	//调用顺序：构造函数调用insert函数。

	binnode<temp>* search(binnode<temp>*& r, temp key);
	void is_found(binnode<temp>*& r, temp k)
	{
		binnode<temp>* p = search(r, k);
		if (p != NULL)
			cout << "is_found:" << p->data;
		else
			cout << "un_found";
	}

	binnode<temp>* get_root()
	{
		return this->root;
	}

	void release(binnode<temp>* r);
	~BST();
	//调用顺序：析构函数调用release函数。

	void delete_node(binnode<temp>*& r);
	bool delete_key(binnode<temp>*& r, temp key);
	//调用顺序：delete_key函数调用delete_node函数。

	void inorder_print(binnode<temp>*p);
private:
	binnode<temp>* root;
};

template<class temp>
BST<temp>::BST(temp r[], int n)
{
	this->root = NULL;
	for (int i = 0; i < n; i++)
	{
		binnode<temp>* s = new binnode<temp>;
		s->data = r[i];
		s->leftchild = s->rightchild = NULL;
		insert_bst(this->root, s);
	}
}
template<class temp>
void BST<temp>::insert_bst(binnode<temp>*& r, binnode<temp>* s)
{
	if (r == NULL)
		r = s;
	else if (s->data < r->data)
		insert_bst(r->leftchild, s);
	else
		insert_bst(r->rightchild, s);
}

template<class temp>
binnode<temp>* BST<temp>::search
(binnode<temp>*& r, temp k)
{
	if (r == NULL)
		return NULL;
	if (k == r->data)
		return r;
	else if (k < r->data)
		return search(r->leftchild, k);
	else
		return search(r->rightchild, k);
}


template<class temp>
void BST<temp>::release(binnode<temp>* r)
{
	if (r != NULL)
	{
		release(r->leftchild);
		release(r->rightchild);
		delete r;
	}
}
template<class temp>
BST<temp>::~BST()
{
	release(this->root);
}


template<class temp>
bool BST<temp>::delete_key(binnode<temp>*&r,temp k)
{
	if (r == NULL)
		return false;
	else
	{
		if (k == r->data)
		{
			delete_node(r);
			return true;
		}
		else if (k < r->data)
			return delete_key(r->leftchild, k);
		else
			return delete_key(r->rightchild, k);

	}
}
template<class temp>
void BST<temp>::delete_node(binnode<temp>*& r)
{
	binnode<temp>* q, * s;
	if (r->leftchild == NULL)
	{
		q = r;
		r = r->rightchild;
		delete q;
	}
	else if (r->rightchild == NULL)
	{
		q = r;
		r = r->leftchild;
		delete q;
	}
	else
	{
		q = r;
		s = r->leftchild;
		while (s->rightchild != NULL)
		{
			q = s;
			s = s->rightchild;
		}
		r->data = s->data;
		if (q != r)
			q->rightchild = s->leftchild;
		else
			r->leftchild = s->leftchild;
		delete s;
	}
}


template<class temp>
void BST<temp>::inorder_print(binnode<temp>* p)
{
	if(p != NULL)
	{
		inorder_print(p->leftchild);
		cout << p->data;
		inorder_print(p->rightchild);
	}
}

int main()
{
	system("color 0A");
	student stu[5] = { {1,"zhang"},{2,"wang"},{3,"li"},{4,"zhao"},{5,"liu"} };
	BST<student>bst(stu, 5);
	binnode<student>* p = bst.get_root();
	bst.inorder_print(p);

	student s(2, "wang");

	bst.is_found(p, s);

	bst.delete_key(p, s);
	bst.inorder_print(p);

	bst.is_found(p, s);

	return 0;
}

运行结果：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/630742.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

全新出品！阿里 P5 工程师~P8 架构师晋升路线揭秘

全新出品！阿里 P5 工程师~P8 架构师晋升路线揭秘

阿里巴巴终于公开了从初级程序员到架构师的学习路线图&#xff0c;这里相对应的基本上就是从P5到P8的晋升体系&#xff01;今天老师将会带着大家从初级程序员开始一点点分享整个晋升体系&#xff01; 职级&#xff1a;初级程序员 薪资&#xff1a;6-12K 开发年限&#xff1a;0-…
阅读更多...
PureComponent和Component的区别和底层处理机制

PureComponent和Component的区别和底层处理机制

PureComponent和Component都是React中的组件类&#xff0c;但它们在实现细节和使用上有些差别。 Component是React中定义组件的基类&#xff0c;它的shouldComponentUpdate方法默认返回true&#xff0c;也就是说&#xff0c;每次调用setState或forceUpdate方法都会引发组件重新…
阅读更多...
代码随想录第55天

代码随想录第55天

1.判断子序列&#xff1a; 动态规划五部曲分析如下&#xff1a; 确定dp数组&#xff08;dp table&#xff09;以及下标的含义 dp[i][j] 表示以下标i-1为结尾的字符串s&#xff0c;和以下标j-1为结尾的字符串t&#xff0c;相同子序列的长度为dp[i][j]。 注意这里是判断s是否…
阅读更多...
百度新闻源调整：自媒体权重降低，官方媒体优势突显

百度新闻源调整：自媒体权重降低，官方媒体优势突显

我是卢松松&#xff0c;点点上面的头像&#xff0c;欢迎关注我哦&#xff01; 根据黑猫发稿的消息&#xff0c;自6月1日起&#xff0c;百度新闻源取消了大部分自媒体新闻源的收录&#xff0c;包括搜狐自媒体、企鹅号、网易号&#xff0c;甚至百度自己的百家号也受到了影响。 …
阅读更多...
X2000 Linux 低功耗

X2000 Linux 低功耗

一、进入休眠 当系统启动后&#xff0c;在命令终端输入&#xff1a; echo mem> /sys/power/state 即可立即进入休眠&#xff0c;功耗也随之降低。 二、配置中断唤醒GPIO 1、确认kernel默认配置文件 进入到/tools/iconfigtool/IConfigToolApp/路径下&#xff0c;执行./…
阅读更多...
【Pm4py第四讲】关于Conversion

【Pm4py第四讲】关于Conversion

本节用于介绍pm4py中的转换函数&#xff0c;包括日志、事件流、数据块的转换、Petei网、流程树、BPMN的转换、可达图、面向对象日志等。 1.函数概述 本次主要介绍Pm4py中一些常见的转换函数&#xff0c;总览如下表&#xff1a; 函数名说明convert_log_to_networkx&#xff08;…
阅读更多...
Java（30天拿下---第一天）

Java（30天拿下---第一天）

Java开发&#xff08;30天拿下---第一天&#xff09; 一 hello world以及JDK,JRE,JVM二 转义字符三 注释四 代码规范五 DOS命令&#xff08;了解&#xff09;六 变量1.加号的使用2.数据类型整型浮点型字符类型布尔类型自动类型转换强制类型转换String类型 七 API文档 一 hello …
阅读更多...
React | Redux的使用详解

React | Redux的使用详解

✨ 个人主页&#xff1a;CoderHing &#x1f5a5;️ React.js专栏&#xff1a;React.js Redux的使用详解 &#x1f64b;‍♂️ 个人简介&#xff1a;一个不甘平庸的平凡人&#x1f36c; &#x1f4ab; 系列专栏&#xff1a;吊打面试官系列 16天学会Vue 7天学会微信小程序 N…
阅读更多...
亚马逊云科技Serverless数据分析，助力猎豹移动构建更高性价比数据仓库

亚马逊云科技Serverless数据分析，助力猎豹移动构建更高性价比数据仓库

也许你也听过这样一句话&#xff1a;“21世纪什么最贵&#xff1f;人才&#xff01;”当数字经济全面席卷而来&#xff0c;这个问题的答案不可置否地变为了“数据”。通过数据分析获取近乎实时的洞察&#xff0c;以驱动业务的全流程&#xff0c;是企业数字化转型的必经之路。借…
阅读更多...
【文末送书】微服务拆分规范

【文末送书】微服务拆分规范

目录 一. &#x1f981; 什么是微服务&#xff1f;二. &#x1f981; 拆分模型Ⅰ. 压力模型拆分1. 垂直拆分&#xff08;Vertical Decomposition&#xff09;2. 水平拆分&#xff08;Horizontal Decomposition&#xff09;3. 动态拆分&#xff08;Dynamic Decomposition&#x…
阅读更多...
初识网络之http协议

初识网络之http协议

目录 一、http协议含义 二、 认识URL 三、urlencode与urldecode 1. urlencode 2. urldecode 四、http协议响应与请求格式 1. http协议请求格式 2.http协议响应格式 3. http请求实际形式 3.1 程序准备 3.2 浏览器发起请求 3.3 请求行内容 3.4 请求报头内容 4. htt…
阅读更多...
2022年国赛高教杯数学建模E题小批量物料的生产安排解题全过程文档及程序

2022年国赛高教杯数学建模E题小批量物料的生产安排解题全过程文档及程序

2022年国赛高教杯数学建模 E题 小批量物料的生产安排 原题再现 某电子产品制造企业面临以下问题&#xff1a;在多品种小批量的物料生产中&#xff0c;事先无法知道物料的实际需求量。企业希望运用数学方法&#xff0c;分析已有的历史数据&#xff0c;建立数学模型&#xff0c…
阅读更多...
mysql联合索引详解

mysql联合索引详解

比较简单的是单列索引&#xff08;btree&#xff09;。遇到多条件查询时&#xff0c;不可避免会使用到多列索引。联合索引又叫复合索引。 btree结构如下&#xff1a; 每一个磁盘块在mysql中是一个页&#xff0c;页大小是固定的&#xff0c;mysql innodb的默认的页大小是16k&a…
阅读更多...
【工作中遇到的性能优化问题】

【工作中遇到的性能优化问题】

项目场景&#xff1a; 页面左侧有一列表数据&#xff0c;点击列表项会查对应的表格数据和表单信息&#xff08;表单是根据数据配置生成的&#xff09;&#xff0c;并在右侧展示。如果数据量大&#xff0c;则非常卡。 需要对此页面进行优化。 问题描述 问题一、加载左侧数据时…
阅读更多...
systemV的工作原理+原理代码

systemV的工作原理+原理代码

概念 我们知道进程间的通信有管道的方式进程通信管道制作_云的小站的博客-CSDN博客 但是我们的管道通信其实属于一种取巧的方式&#xff0c;利用了打开的文件可读写的特性上&#xff0c;两个进程对此分别进行读写操作就会产生所谓的通信现象&#xff0c;但是外面的管道依旧得…
阅读更多...
【社区图书】快速入门go程序开发——《Go程序开发实战宝典》书评

【社区图书】快速入门go程序开发——《Go程序开发实战宝典》书评

《Go程序开发实战宝典》书评 一、介绍二、简要概述三、内容分析3.1、第一部分&#xff1a;Go语言基础知识3.2、第二部分&#xff1a;介绍服务端开发经常需要处理的问题3.3、第三部分&#xff1a;Go语言开发实践实战案例 四、我的看法和评价4.1、对本书整体评价4.2、我对这本书的…
阅读更多...
Office Visio 2021安装

Office Visio 2021安装

哈喽&#xff0c;大家好。今天一起学习的是Visio 2021的安装&#xff0c;这是一个绘制流程图的软件&#xff0c;用有效的绘图表达信息&#xff0c;比任何文字都更加形象和直观。Office Visio 是office软件系列中负责绘制流程图和示意图的软件&#xff0c;便于IT和商务人员就复杂…
阅读更多...
Vue.js 中的插槽和动态组件

Vue.js 中的插槽和动态组件

Vue.js 中的插槽和动态组件 Vue.js 是一款流行的 JavaScript 框架&#xff0c;它提供了一种简单而灵活的方式来构建交互式 Web 应用程序。在 Vue.js 中&#xff0c;插槽和动态组件是两个常用的概念。它们可以帮助开发者更方便地组织和管理组件的结构和行为。但是这两个概念有什…
阅读更多...
（opencv）图像几何变换——平移

（opencv）图像几何变换——平移

图像的平移操作是将图像的所有像素坐标进行水平或垂直方向移动&#xff0c;也就是将所有像素点按照给定的偏移量在水平方向沿x轴、垂直方向上沿y轴移动。平移变换分为两种类型&#xff1a;图像大小变化与图像大小不变。第一种类型保证图像平移的完整信息&#xff0c;第二种图像…
阅读更多...
Vue.js 中的 $refs 和 $emit 有什么关系？

Vue.js 中的 $refs 和 $emit 有什么关系？

Vue.js 中的 $refs 和 $emit 有什么关系&#xff1f; 在 Vue.js 中&#xff0c;$refs 和 $emit 都是非常常用的 API。$refs 用于访问组件、元素和子组件等&#xff0c;而 $emit 则用于在组件之间进行通信。本文将会从语法、使用方式、适用场景等方面进行介绍&#xff0c;并探讨…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023