一、蒙特卡洛仿真

蒙特卡洛仿真的基本原理是通过生成大量的随机样本，以近似地估计实际事件的概率和预测结果。 它是以蒙特卡洛赌场命名的，因为它使用随机数和概率统计的方法来模拟现实世界中的各种情况和结果，就像在赌场中抛骰子或发牌一样。

缺点：收敛精度 $\epsilon \propto \frac{1}{\sqrt{n}}$, 收敛速度慢!

优点：和问题的维数无关，只要边界可以描述，就都可以求。

###【例1】圆周率计算

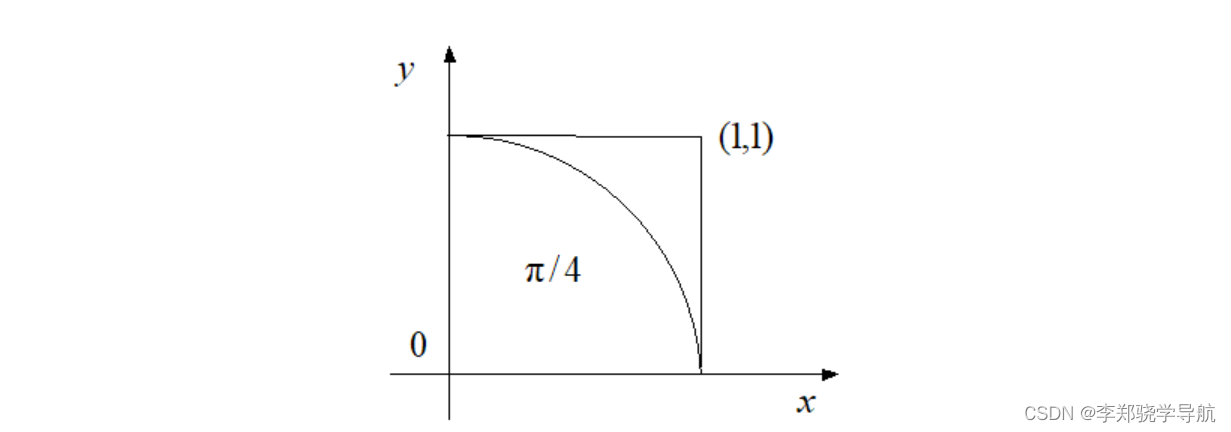
我们都知道, 单位圆围成的面积为 $\pi$, 若以圆心为原点 建立平面直角坐标系, 则它在第一象限内的面积为 $\pi /4$, 即有：
$${\int }_0^1{\int }_0^{\sqrt{1-y^2}}1\mathrm{d}x\mathrm{d}y=\pi /4$$

Matlab仿真：

n = 1000000;				% 十万个点
p = unifrnd(0,1,2,n);		 % 在 0~1 区间均匀随机分布，生成二维点
PI = 4*sum(sum(p.^2)<1)/n     % 求出在四分之一圆内的比例，再乘 4

结果：PI = 3.141092 ，前三个数字是准确的。计算机仿真，可以实现均匀分布，如果是现实仿真，保证不了均匀分布，效果会更差。

【例2】体积计算

在单位球体内偏离中心 0.25 的位置挖去一个半径为 0.25 的柱体 (参见图), 试求该球体剩余部分的体积。

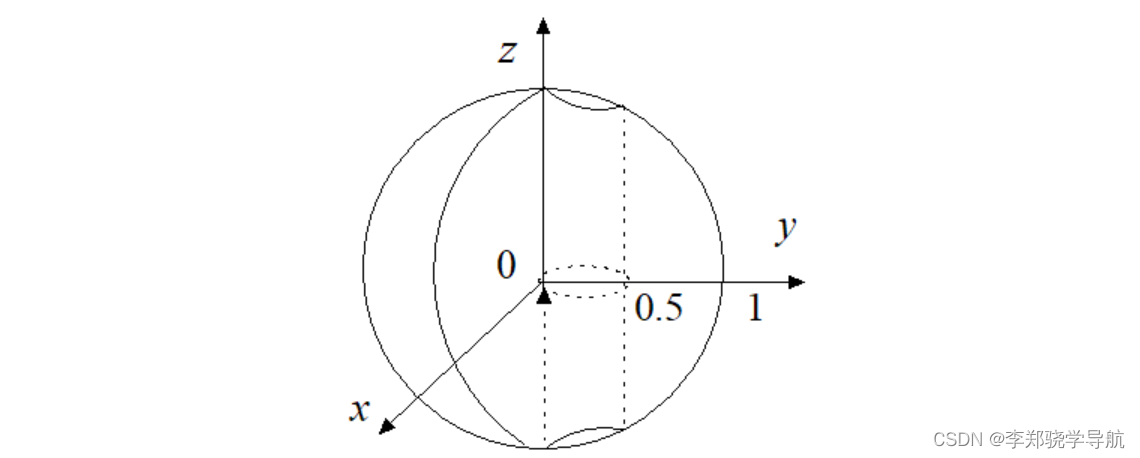
用一个立方体，包住这个球，生成均匀分布的随机点，

Matlab仿真：

n = 100000;
p = unifrnd(-1,1,3,n);
V = 2^3*sum(sum(p.^2)<1&(p(1,:).^2 + (p(2,:)-0.25).^2)>0.25^2)/n

结果：V = 3.812905。

【例3】二维随机向量的非线性变换/概论传播

已知 $x$ 的分布，求 $2x$ 的分布比较简单，因为属于线性变换。如果是求 $x^2+2x+e^x$ 就比较难了。用仿真的方法求结果的分布函数也比较难，但如果只追求对其粗略的了解，比如均值、方差，可以实现。

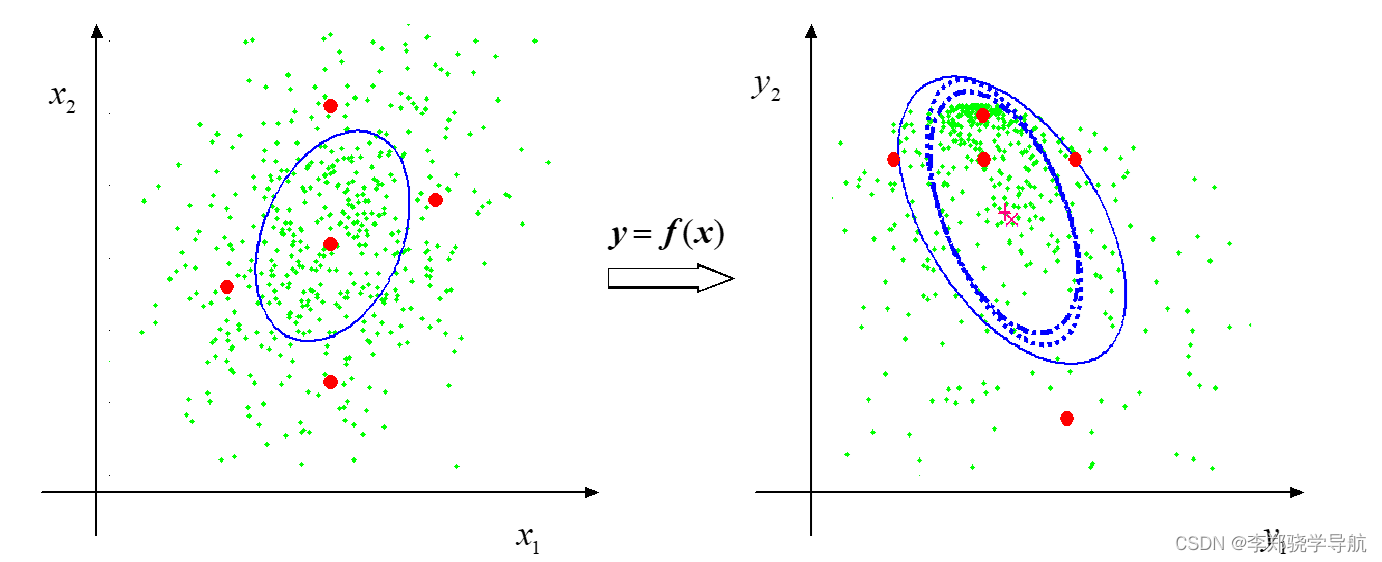
现在有如下的函数，输入 $x_1$、$x_2$ ，转化到 $y_1$、$y_2$ 都是非线性函数， 二维方差是一个对称正定阵，分布是一个椭圆，椭圆就是一个长轴一个短轴，总可以分解得到。
$$\{\begin{array}{l}{y}_1=\left(x_1-1\right)\cdot \left(x_2-0.2\right)\\ y_2=-{\left(x_1-1\right)}^2\end{array}E\left[x{x}^{\mathrm{T}}\right]=\left[\begin{array}{cc}1& 0.42\\ 0.42& 2\end{array}\right]$$
可以画出下面的图。左边每个绿点代表一个向量，共500个点，满足蓝色的方差椭圆分布。经过上面的非线性函数得到右边的点，可由点的分布统计得右边的均值、方差。无穷个点得到的真实的方差椭圆是图中的实线，统计出来的是十字线，统计值和真实值算比较接近的了。

用5个红点也能变换过去，也能统计均值和方差，画出误差椭圆是叉线，与500个绿点得到的十字线几乎重合。

二、UT变换

1、线性系统的UT变换

假设随机向量的线性变换关系 $\mathbf{y}=\mathbf{F}\mathbf{x}$
$$\{\begin{array}{l}\overline{\mathbf{x}}=E[\mathbf{x}]\\ {\mathbf{P}}_x=E[(\mathbf{x}-\overline{\mathbf{x}})(\mathbf{x}-\overline{\mathbf{x}}{)}^{\mathrm{T}}]\end{array}⟹\{\begin{array}{l}\overline{\mathbf{y}}=\mathbf{F}\overline{\mathbf{x}}\\ {\mathbf{P}}_y=\mathbf{F}{\mathbf{P}}_x{\mathbf{F}}^{\mathrm{T}}\\ {\mathbf{P}}_{xy}={\mathbf{P}}_x{\mathbf{F}}^{\mathrm{T}}\end{array}$$

1.方差阵的Cholesky分解

${\mathbf{P}}_x=\mathbf{A}{\mathbf{A}}^{\mathrm{T}}$ 记 $\sqrt{{\mathbf{P}}_x}=\mathbf{A}\left[\begin{array}{cc}1& 2\\ 2& 13\end{array}\right]=\left[\begin{array}{ll}1& 0\\ 2& 3\end{array}\right]$

如此，P 就可以写成：${\mathbf{P}}_x=\sqrt{{\mathbf{P}}_x}{\sqrt{{\mathbf{P}}_x}}^{\mathrm{T}}={\sum }_{i=1}^n{\left(\sqrt{{\mathbf{P}}_x}\right)}_i{\left(\sqrt{{\mathbf{P}}_x}\right)}_i^{\mathrm{T}}$ ，向量累加和的形式。

如 $\begin{array}{l}\left[\begin{array}{cc}1& 2\\ 2& 13\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 2& 3\end{array}\right]\left[\begin{array}{ll}1& 2\\ 0& 3\end{array}\right]=\left[\begin{array}{l}1\\ 2\end{array}\right]\left[\begin{array}{ll}1& 2\end{array}\right]+\left[\begin{array}{l}0\\ 3\end{array}\right]\left[\begin{array}{ll}0& 3\end{array}\right]\end{array}$

向量就是图上的点，$p$ 如果是高维的，$\sqrt{\mathbf{P}}$ 里的每一列就代表其中一个点。

2.输入近似成有限个（n个）Sigma点的估计形式

$$\{\begin{array}{l}\overline{\mathbf{x}}=\underset{k\to \infty }{\lim }\frac{1}{k}{\sum }_{i=1}^k{\chi }_i\approx \frac{1}{n}{\sum }_{i=1}^n{\chi }_i\\ {\mathbf{P}}_x=\underset{k\to \infty }{\lim }\frac{1}{k}{\sum }_{i=1}^k\left({\chi }_i-\bar{x}\right){\left({\chi }_i-\overline{\mathbf{x}}\right)}^{\mathrm{T}}\approx \frac{1}{n}{\sum }_{i=1}^n\left({\chi }_i-\overline{\mathbf{x}}\right){\left({\chi }_i-\overline{\mathbf{x}}\right)}^{\mathrm{T}}\end{array}$$

式中的 $P_x$ 与上面 ${\mathbf{P}}_x={\sum }_{i=1}^n{\left(\sqrt{{\mathbf{P}}_x}\right)}_i{\left(\sqrt{{\mathbf{P}}_x}\right)}_i^{\mathrm{T}}$ 的形式对应，比较, 可得 $\frac{1}{\sqrt{n}}\left({\mathbf{\chi }}_i-\overline{\mathbf{x}}\right)=\pm {\left(\sqrt{{\mathbf{P}}_x}\right)}_i$ ，即 ${\chi }_i=\overline{\mathbf{x}}\pm {\left(\sqrt{n{\mathbf{P}}_x}\right)}_i$ ，sigma点就是在均值的地方加减 ${\left(\sqrt{n{\mathbf{P}}_x}\right)}_i$

3.输入近似成有限个（2n个）Sigma点的估计形式

输入取上一步求得的sigma点，带入线性函数中，得：
$$\{\begin{array}{l}\overline{\mathbf{x}}=\frac{1}{2n}{\sum }_{i=1}^{2n}{\chi }_i\\ {\mathbf{P}}_x=\frac{1}{2n}{\sum }_{i=1}^{2n}\left({\chi }_i-\overline{\mathbf{x}}\right){\left({\chi }_i-\overline{\mathbf{x}}\right)}^{\mathrm{T}}\end{array}$$
记Sigma点组成的输入矩阵：$\chi =\left[[\overline{\mathbf{x}}{]}_n+\sqrt{n{\mathbf{P}}_x}[\overline{\mathbf{x}}{]}_n-\sqrt{n{\mathbf{P}}_x}\right]$ ，n*2n矩阵

得Sigma点组成的输出矩阵：$\mathbf{\eta }=\left[[\mathbf{F}\overline{\mathbf{x}}{]}_n+\mathbf{F}\sqrt{n{\mathbf{P}}_x}[\mathbf{F}\overline{\mathbf{x}}{]}_n-\mathbf{F}\sqrt{n{\mathbf{P}}_x}\right]$

4.由输入输出Sigma点计算传播统计特征

$$\{\begin{array}{l}\overline{\mathbf{y}}=\frac{1}{2n}{\sum }_{i=1}^{2n}{\mathbf{\eta }}_i=\frac{1}{2n}{\sum }_{i=1}^{2n}\mathbf{F}\overline{\mathbf{x}}=\mathbf{F}\overline{\mathbf{x}}\\ {\mathbf{P}}_y=\frac{1}{2n}{\sum }_{i=1}^{2n}\left({\mathbf{\eta }}_i-\overline{\mathbf{y}}\right){\left({\mathbf{\eta }}_i-\overline{\mathbf{y}}\right)}^{\mathrm{T}}=\frac{1}{2n}{\sum }_{i=1}^{2n}\left(\mathbf{F}\sqrt{n{\mathbf{P}}_x}\right){\left(\mathbf{F}\sqrt{n{\mathbf{P}}_x}\right)}^{\mathrm{T}}={\mathbf{F}}_x{\mathbf{F}}^{\mathrm{T}}\\ {\mathbf{P}}_{xy}=\frac{1}{2n}{\sum }_{i=1}^{2n}\left({\mathbf{x}}_i-\overline{\mathbf{x}}\right){\left({\mathbf{\eta }}_i-\overline{\mathbf{y}}\right)}^{\mathrm{T}}=\frac{1}{2n}{\sum }_{i=1}^{2n}\left(\sqrt{n{\mathbf{P}}_x}\right){\left(\mathbf{F}\sqrt{n{\mathbf{P}}_x}\right)}^{\mathrm{T}}={\mathbf{P}}_x{\mathbf{F}}^{\mathrm{T}}\end{array}$$

与理论结果一致，精确地捕获了输出的一、二阶矩。

2、非线性函数的UT变换

将这种操作放到非线性函数 $y=f(x)$ 中：只是输入的Sigma点要带到非线性函数中算，输出的操作和线性的一致，只是符号变为约等于号。
$$\{\begin{array}{l}\mathbf{\chi }=\left[[\overline{\mathbf{x}}{]}_n+\sqrt{n{\mathbf{P}}_x}[\overline{\mathbf{x}}{]}_n-\sqrt{n{\mathbf{P}}_x}\right]\\ {\mathbf{\eta }}_i=\mathbf{f}\left({\chi }_i\right)\\ \overline{\mathbf{y}}\approx 1/(2n)\cdot {\sum }_{i=1}^{2n}{\mathbf{\eta }}_i\\ {\mathbf{P}}_y\approx 1/(2n)\cdot {\sum }_{i=1}^{2n}\left({\mathbf{\eta }}_i-\overline{\mathbf{y}}\right){\left({\mathbf{\eta }}_i-\overline{\mathbf{y}}\right)}^{\mathrm{T}}\\ {\mathbf{P}}_{xy}\approx 1/(2n)\cdot {\sum }_{i=1}^{2n}\left({\chi }_i-\overline{\mathbf{x}}\right){\left({\mathbf{\eta }}_i-\overline{\mathbf{y}}\right)}^{\mathrm{T}}\end{array}$$
可以改成更一般的形式：

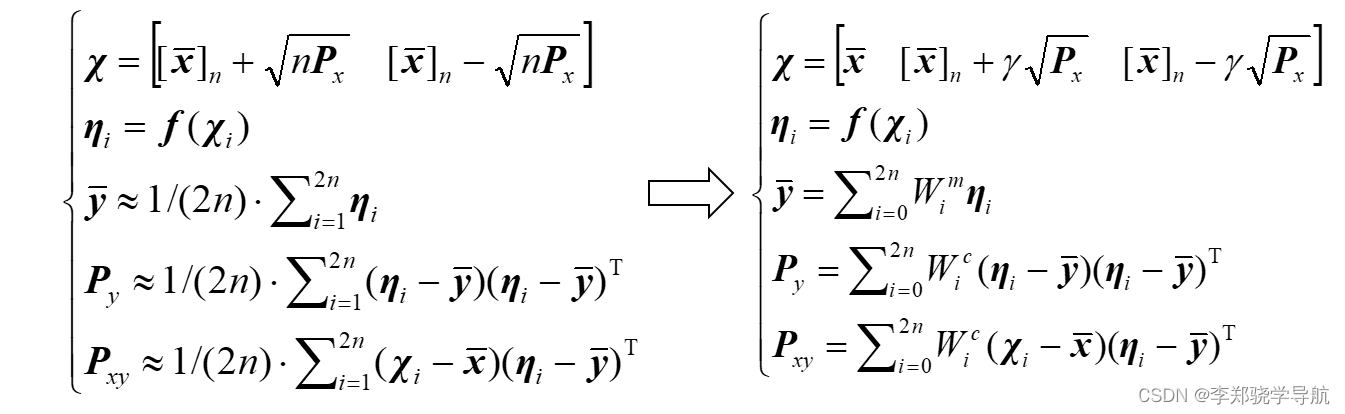
其中：

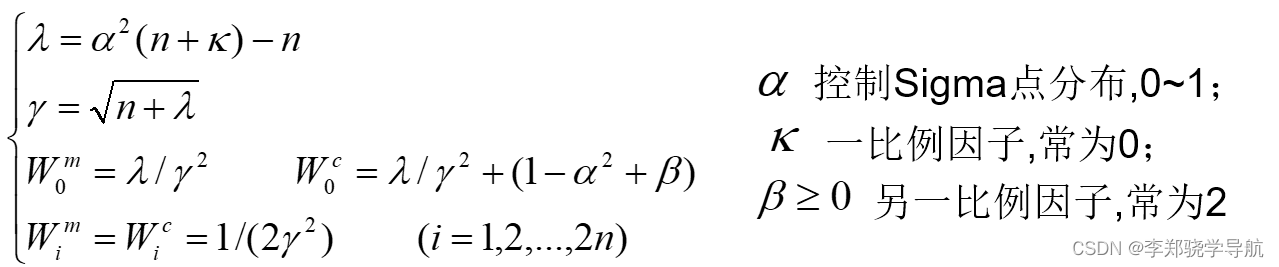
非线性如果比较严重，$\alpha$ 就应该取的比较小，使展开的点集中上次均值的附近。

EKF需要泰勒级数展开；UKF不需要，只要表达式能知道能运算就行了，点总可以运算得到结果，总可以进行统计

3、UT变换图示

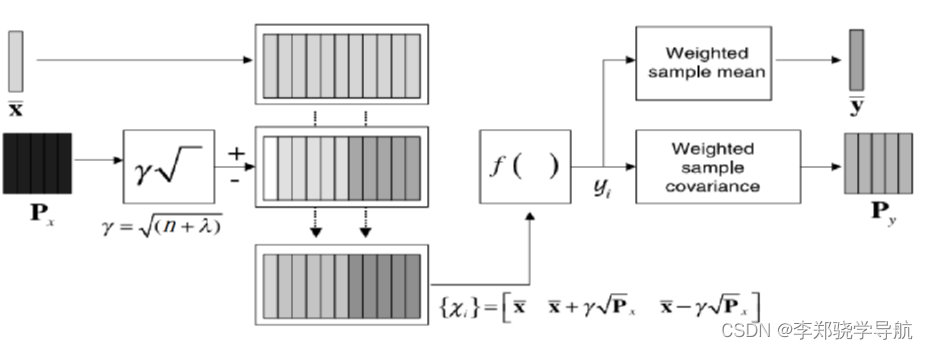
三、UKF滤波

系统模型
$$\{\begin{array}{l}{\mathbf{x}}_k=\mathbf{f}\left({\mathbf{x}}_{k-1}\right)+{\mathbf{B}}_{k-1}{\mathbf{w}}_{k-1}\\ {\mathbf{y}}_k=\mathbf{h}\left({\mathbf{x}}_k\right)+{\mathbf{v}}_k\end{array}$$
滤波框架
$$\{\begin{array}{l}{\mathbf{K}}_k={\mathbf{P}}_{xy,k/k-1}{\mathbf{P}}_{y,k/k-1}^{-1}\\ {\hat{\mathbf{x}}}_k={\hat{\mathbf{x}}}_{k/k-1}+{\mathbf{K}}_k\left({\mathbf{y}}_k-{\hat{\mathbf{y}}}_{k/k-1}\right)\\ {\mathbf{P}}_{x,k}={\mathbf{P}}_{x,k/k-1}-{\mathbf{K}}_k{\mathbf{P}}_{y,k/k-1}{\mathbf{K}}_k^{\mathrm{T}}\end{array}$$
状态预测UT变换
$$\{\begin{array}{l}{\mathbf{\chi }}_{k-1}=\left[\begin{array}{lll}{\hat{\mathbf{x}}}_{k-1}& {\left[{\hat{\mathbf{x}}}_{k-1}\right]}_n+\gamma \sqrt{{\mathbf{P}}_{x,k-1}}& {\left[{\hat{\mathbf{x}}}_{k-1}\right]}_n-\gamma \sqrt{{\mathbf{P}}_{x,k-1}}\end{array}\right]\\ {\chi }_{i,k/k-1}^{\ast }=\mathbf{f}\left({\mathbf{\chi }}_{i,k-1}\right)\\ {\hat{\mathbf{x}}}_{k/k-1}={\sum }_{i=0}^{2n}{W}_i^m{\chi }_{i,k/k-1}^{\ast }\\ {\mathbf{P}}_{x,k/k-1}={\sum }_{i=0}^{2n}{W}_i^c\left({\chi }_{i,k/k-1}^{\ast }-{\hat{\mathbf{x}}}_{k/k-1}\right){\left({\chi }_{i,k/k-1}^{\ast }-{\hat{\mathbf{x}}}_{k/k-1}\right)}^{\mathrm{T}}+{\mathbf{B}}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{B}}_{k-1}^{\mathrm{T}}\end{array}$$
量测预测UT变换
$$\{\begin{array}{l}{\mathbf{\chi }}_{k/k-1}=\left[\begin{array}{lll}{\hat{\mathbf{x}}}_{k/k-1}& {\left[{\hat{\mathbf{x}}}_{k/k-1}\right]}_n+\gamma \sqrt{{\mathbf{P}}_{x,k/k-1}}& {\left[{\hat{\mathbf{x}}}_{k/k-1}\right]}_n-\gamma \sqrt{{\mathbf{P}}_{x,k/k-1}}\end{array}\right]\\ {\mathbf{\eta }}_{i,k/k-1}=\mathbf{h}\left({\chi }_{i,k/k-1}\right)\\ {\hat{\mathbf{y}}}_{k/k-1}={\sum }_{i=0}^{2n}{W}_i^m{\mathbf{\eta }}_{i,k/k-1}\\ {\mathbf{P}}_{y,k/k-1}={\sum }_{i=0}^{2n}{W}_i^c\left({\mathbf{\eta }}_{i,k/k-1}-{\hat{\mathbf{y}}}_{k/k-1}\right){\left({\mathbf{\eta }}_{i,k/k-1}-{\hat{\mathbf{y}}}_{k/k-1}\right)}^{\mathrm{T}}+{\mathbf{R}}_k\\ {\mathbf{P}}_{xy,k/k-1}={\sum }_{i=0}^{2n}{W}_i^c\left({\mathbf{\chi }}_{i,k/k-1}-{\hat{\mathbf{x}}}_{k/k-1}\right){\left({\mathbf{\eta }}_{i,k/k-1}-{\hat{\mathbf{y}}}_{k/k-1}\right)}^{\mathrm{T}}\end{array}$$
每个都实现，带到框架里，完成UKF时间更新、量测更新

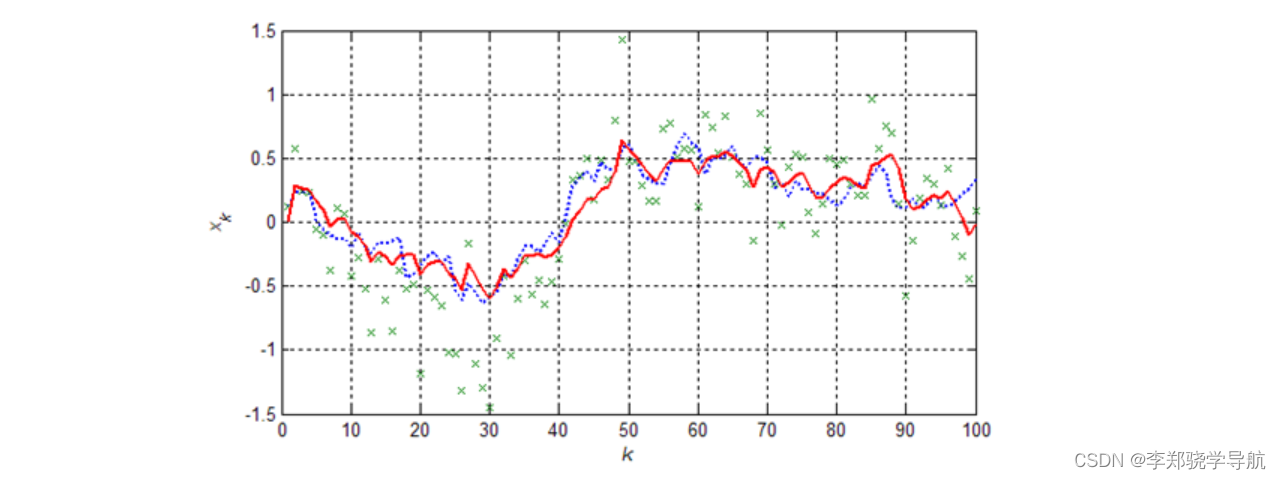
【例1】一维非线性随机系统

$$\{\begin{array}{l}{x}_k=\sin \left(x_{k-1}\right)+w_{k-1}\\ y_k=\{\begin{array}{ll}{x}_k+v_k& x_k>0\\ 2x_k+v_k& x_k\le 0\end{array}{w}_k\sim WN\left(0,0.1^2\right)v_k\sim WN\left(0,0.3^2\right)\end{array}$$

仿真结果：滤波效果与初值的选择关系密切

【例2】针对非常复杂的非线性系统模型

近似非线性概率传播 比近似非线性函数（泰勒展开线性化）更简单，此时UKF滤波比EKF滤波更具优势。

比如惯导大失准角误差模型
$$\{\begin{array}{l}\dot{\mathbf{\alpha }}={\mathbf{C}}_{\omega }^{-1}\left[\left(\mathbf{I}-{\mathbf{C}}_n^{n^{\prime }}\right){\mathbf{\omega }}_{in}^n-{\mathbf{\epsilon }}^{n^{\prime }}\right]\\ \delta {\dot{\mathbf{v}}}^n=\left[\mathbf{I}-{\left({\mathbf{C}}_n^{n^{\prime }}\right)}^{\mathrm{T}}\right]{\tilde{\mathbf{f}}}_{sf}^{n^{\prime }}+{\left({\mathbf{C}}_n^{n^{\prime }}\right)}^{\mathrm{T}}{\nabla }^{n^{\prime }}\end{array}$$
其中：
$${\mathbf{C}}_{\omega }^{-1}=\frac{1}{c{\alpha }_x}\left[\begin{array}{ccc}c{\alpha }_{y}c{\alpha }_x& 0& s{\alpha }_{y}c{\alpha }_x\\ s{\alpha }_{y}s{\alpha }_x& c{\alpha }_x& -c{\alpha }_{y}s{\alpha }_x\\ -s{\alpha }_y& 0& c{\alpha }_y\end{array}\right]$$

$${\mathbf{C}}_n^{n^{\prime }}=\left[\begin{array}{ccc}c{\alpha }_{y}c{\alpha }_z-s{\alpha }_{y}s{\alpha }_{x}s{\alpha }_z& c{\alpha }_{y}s{\alpha }_z+s{\alpha }_{y}s{\alpha }_{x}c{\alpha }_z& -s{\alpha }_{y}c{\alpha }_x\\ -c{\alpha }_{x}s{\alpha }_z& c{\alpha }_{x}c{\alpha }_z& s{\alpha }_x\\ s{\alpha }_{y}c{\alpha }_z+c{\alpha }_{y}s{\alpha }_{x}s{\alpha }_z& s{\alpha }_{y}s{\alpha }_z-c{\alpha }_{y}s{\alpha }_{x}c{\alpha }_z& c{\alpha }_{y}c{\alpha }_x\end{array}\right]$$

方程如此复杂，想进行泰勒级数展开很困难，可以用UKF。