求解线性方程组




右乘向量/矩阵
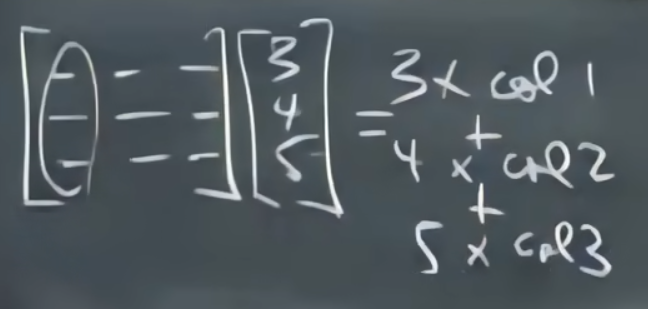
把左边的矩阵拆成一个个列向量,右边的向量表示对左边列向量组的线性组合。
[ c o l 1 c o l 2 c o l 3 ] [ 3 4 5 ] = [ 3 c o l 1 + 4 c o l 2 + 5 c o l 3 ] \left[\begin{array}{c} col_{1} & col_{2} & col_{3} \end{array}\right] \left[\begin{array}{c} 3 \\ 4 \\ 5 \end{array}\right]= \left[\begin{array}{c} 3col_1+4col_2+5col_3 \end{array}\right] [col1col2col3] 345 =[3col1+4col2+5col3]
右边的矩阵:把左边的矩阵看作一个个列向量
第n行的第m列的数字k 表示结果的第n列采用左边矩阵的第m列乘以k
左乘向量/矩阵
[
1
2
7
]
[
r
o
w
1
r
o
w
2
r
o
w
3
]
=
[
1
r
o
w
1
+
2
r
o
w
2
+
7
r
o
w
3
]
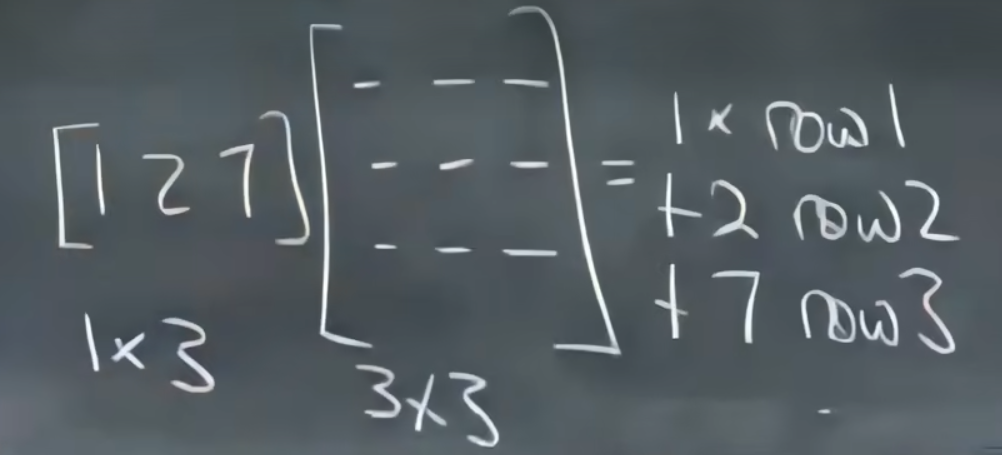
\left[\begin{array}{c} 1 & 2 & 7 \end{array}\right] \left[\begin{array}{c} row_1 \\ row_2 \\ row_3 \end{array}\right]= \left[\begin{array}{c} 1row_1+2row_2+7row_3 \end{array}\right]
[127]
row1row2row3
=[1row1+2row2+7row3]
左边的矩阵:把右边的矩阵看作一个个行向量
第n行的第m列的数字k 表示结果的第n行采用右边矩阵的第m行向量乘以k










![[230604] 听力TPO66汇总·上篇| C1 L1 C2|10:20~12:00](https://img-blog.csdnimg.cn/acaa6eb1359e4dd2b54dfbe295160d0e.jpeg)