242.有效的字母异位词

1.题目描述

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

示例：
输入: s = “anagram”, t = “nagaram”
输出: true

输入: s = “rat”, t = “car”
输出: false

详情leetcode链接

2.题解

先看思路哦！

class Solution {
    /**
     * 思路：需要一个额外的数组记录两个字符串每个字母出现的次数，一个次数增加，
     *       一个次数减少；若最后每个数组上每个数字都中和为0则为字母异位词。
     *     1.因为都是小写字母，所以需要定义一个数组record来记录每个字母出现的次数；
     *     2.因为字符a到字符z的ASCII也是26个连续的数，所以数组大小为 26，初始化为0；
     *     3.需要把字符映射到数组也就是哈希表的索引下标上：因为字符a到字符z的ASCII是
     *  26个连续的数值，所以字符a映射为下标0，相应的字符z映射为下标25。
     *     4.再遍历 字符串s的时候，只需要将 s[i] - ‘a’、‘b’等所在的元素做+1 操，同
     *  样在遍历字符串t的时候，对t中出现的字符映射哈希表索引上的数值再做-1的操作。 
     *     5.最后record数组如果有的元素不为零0，即字符串s和t一定是谁多了字符或者谁少
     *  了字符，return false。若record数组所有元素都为零0，说明字符串s和t是字母异位
     *  词，return true。
     * 时间复杂度：O(m+n),分别遍历了字符串s和t，长度设为 m 和 n（补充：因为数组长度与输入参数无关且为常量可看作O(1)可忽略不计,这里的m和n是和输入字符串长度有关，所以为m+n）
     * 空间复杂度：O(1)
     *     
     *
     */
    public boolean isAnagram(String s, String t) {
        int[] record = new int[26];
		//例如字符串s="aee"，字符串t="eae"
		//s.charAt(a)-'a'=0,即recored数组的第一个位置，刚好与a~z相映射
        for (int i = 0; i < s.length(); i++){
            record[s.charAt(i)-'a']++; //charAt()即返回指定索引处的字符，举例字符a返回97。并不需要记住字符a的ASCII，只要求出一个相对数值就可以了
        }

        for (int i = 0; i < t.length(); i++){
            record[t.charAt(i)-'a']--;
        }

        for (int count : record){
            if (count != 0){  // record数组如果有的元素不为零0，说明字符串s和t 一定是谁多了字符或者谁少了字符。
                return false;
            }
        }

        return true; // record数组所有元素都为零0，说明字符串s和t是字母异位词
    }
}

349.两个数组的交集

1.题目描述

给定两个数组 nums1 和 nums2 ，返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

示例 ：
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

详情leetcode链接

2.题解

先看思路哦！

class Solution {

    /**
     * 思路：哈希set
     *      题目中提到输出结果中的每个元素一定是唯一的，即输出的结果的去重的， 同时可以不考虑输出结果的顺序，所以用哈希set做比较合适
     *      首先遍历数组nums1，将nums1映射到set1中。
     *      接着遍历数组2的过程中判断哈希表set1中是否存在该元素，若存在则放到reSet(用于返回的set)中，最后将结果集转为数组返回。
     * 注意：此题也可以使用数组来做哈希的题目，是因为题目都限制了数值的大小。如果本题没有限制数值的大小，就无法使用数组来做哈希表了。
     * 时间复杂度：O(m + n)：假设数组nums1长度为m，nums长度为n。分别遍历
     * 空间复杂度：O(m): 定义了两个set，其大小取决于nums的大小
     *
     */
    public int[] intersection(int[] nums1, int[] nums2) {
        if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) {
            return new int[0];
        }
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> reSet = new HashSet<>();
        //遍历nums1映射到set1
        for (int i: nums1) {
            set1.add(i);
        }

        //遍历nums2过程中判断set1中是否存在该元素，存在放到reSetzh
        for (int i : nums2){
            if (set1.contains(i)){
                reSet.add(i);
            }
        }

        //将结果集转为数组返回
        return reSet.stream().mapToInt(x->x).toArray();

        // //方法2：将结果集转为数组返回
        // int[] array = new int[reSet.size()];
        // int j = 0;
        // for (int i : reSet){
        //     array[j++] = i;
        // }
        // return array;

    }
}

202.快乐数

1.题目描述

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：
输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：
输入：n = 2
输出：false

详情leetcode链接

2.题解

思路(官方题解啊！看了好几遍真难)

• 根据题意确定边界：（1）最终会得到1；（2）最终会进入循环

• 举例1，例如7——>7²=49——>4²+9²=97…（不断循环此过程），如图直到1
  

• 举例2，从 116开始。通过反复通过平方和计算下一个数字，我们最终得到 58，再继续计算之后，我们又回到 58。由于我们回到了一个已经计算过的数字，可以知道有一个循环，因此不可能达到 1。
  

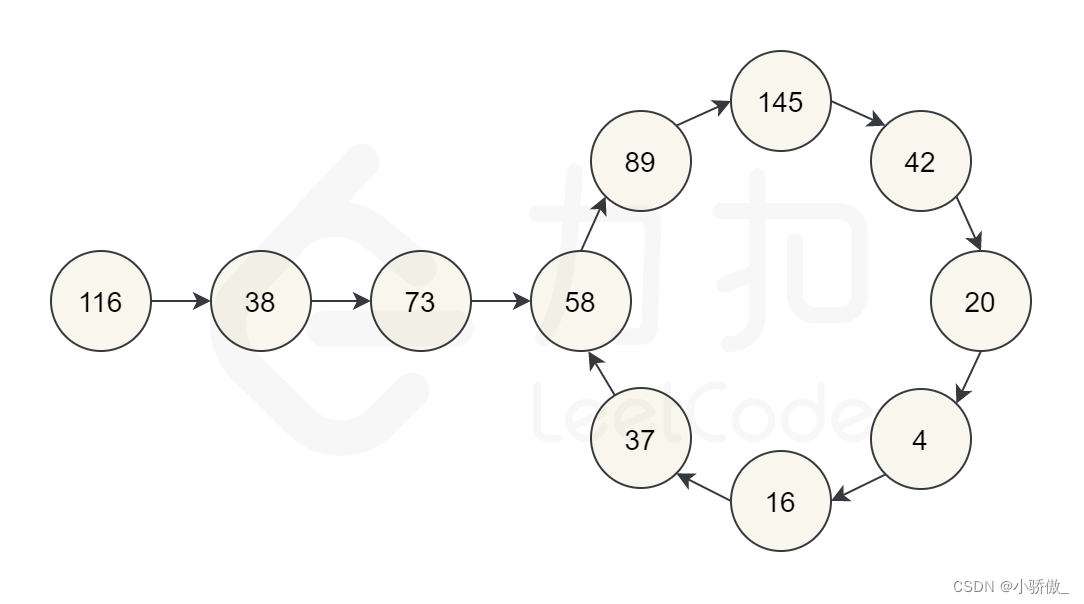
• 所以根据穷举，猜测会有以下三种可能。
  最终会得到 11。
  最终会进入循环。
  值会越来越大，最后接近无穷大。

• 对于第三种情况的思考：我们怎么知道它会继续变大，而不是最终得到 1 呢？可以仔细想一想，每一位数的最大数字的下一位数是多少。
  

• 对于 3位数的数字，它不可能大于 243。这意味着它要么被困在 243以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道 最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种选择。

3.算法

算法分为两部分，我们需要设计和编写代码。

1. 给一个数字 n，它的下一个数字是什么？
2. 按照一系列的数字来判断我们是否进入了一个循环。

第 1 部分我们按照题目的要求做数位分离，求平方和。

第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时，我们都会检查它是否已经在哈希集合中。
如果它不在哈希集合中，我们应该添加它。
如果它在哈希集合中，这意味着我们处于一个循环中，因此应该返回 false。

注意： 我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字。检查数字是否在哈希集合中需要 O(1)的时间，而对于其他数据结构，则需要 O(n)的时间。

4.代码实现

/**
 * 202.快乐数
 * 1）给定一个数n，获取下一个数是什么？
 * 2）按照一系列的数字来判断我们是否进入了一个循环
 * 时间复杂度：O(logn)
 * 空间复杂度：O(logn)
 */
class Solution {

    public static int getNext(int n){
        int totalSum = 0;
        while (n>0){
            int d = n % 10;//取余数获得个位上的数字
            n = n / 10;//取商获得十位上的数字
            totalSum += d*d;
        }
        return totalSum;
    }

    public static boolean isHappy(int n){
        Set<Integer> seen = new HashSet<>();//利用set判断重复
        while (n != 1 &&  !seen.contains(n)){
            seen.add(n);
            n = getNext(n);
        }
        return n==1;
    }
}

5.复杂度分析

时间复杂度： O(243 *3 + log n + loglog n + logloglog n+…) = O(log n)

假设最坏情况，假设小于243的数把每一个数都取到了，那也就是243次判断，每次判断小于3次（因为是三位数以下），所以计算小于243的数的时间复杂度大O是：O（243∗3）

而对于大于243的数，计算下一个数的时间复杂度是：O(log₁₀n)
因为我们正在处理数字中的每位数字，而数字中的位数由 logn 给定。

要计算出总的时间复杂度，我们需要仔细考虑循环中有多少个数字，它们有多大。

我们在上面确定，一旦一个数字低于 243，它就不可能回到 243以上。因此，我们就可以用 243 以下最长循环的长度来代替 243，不过，因为常数无论如何都无关紧要，所以我们不会担心它。

对于高于 243的 n，我们需要考虑循环中每个数高于 243 的成本。通过数学运算，我们可以证明在最坏的情况下，这些成本将是 O(log n) + O(loglog n) + O(logloglog n)…。幸运的是，O(logn) 是占主导地位的部分，而其他部分相比之下都很小（总的来说，它们的总和小于logn），所以我们可以忽略它们。

空间复杂度： O(logn)。

与时间复杂度密切相关的是衡量我们放入哈希集合中的数字以及它们有多大的指标。对于足够大的 n，大部分空间将由 n本身占用。我们可以很容易地优化到 O(243 * 3) = O(1)，方法是只保存集合中小于 243 的数字，因为对于较高的数字，无论如何都不可能返回到它们。

1.两数之和

1.题目描述

详情leetcode链接

2.哈希表法

本题看似简单，实则不简单！思考时主要有以下几个重点：

• 为什么会想到用哈希表？
• 哈希表为什么用map
• 本题map是用来存什么的
• map中的key和value用来存什么的

回忆什么时候使用哈希法： 当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

本题呢，我就需要一个集合来存放我们遍历过的元素，然后在遍历数组的时候去询问这个集合，某元素是否遍历过，也就是 是否出现在这个集合。

此时我们就应该想到使用哈希法了。

根据题意，我们不仅要知道元素有没有遍历过，还要知道这个元素对应的下标，需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适。

再来看一下使用数组和set来做哈希法的局限。

• 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
• set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。

此时就要选择另一种数据结构：map ，map是一种key value的存储结构，可以用key保存数值，用value在保存数值所在的下标。

map目的用来存放我们访问过的元素，因为遍历数组的时候，需要记录我们之前遍历过哪些元素和对应的下标，这样才能找到与当前元素相匹配的（也就是相加等于target）

这道题 我们需要 给出一个元素，判断这个元素是否出现过，如果出现过，返回这个元素的下标。

那么判断元素是否出现，这个元素就要作为key，所以数组中的元素作为key，有key对应的就是value，value用来存下标。

在遍历数组的时候，只需要向map去查询是否有和目前遍历元素匹配的数值，如果有，就找到的匹配对，如果没有，就把目前遍历的元素放进map中，因为map存放的就是我们访问过的元素。

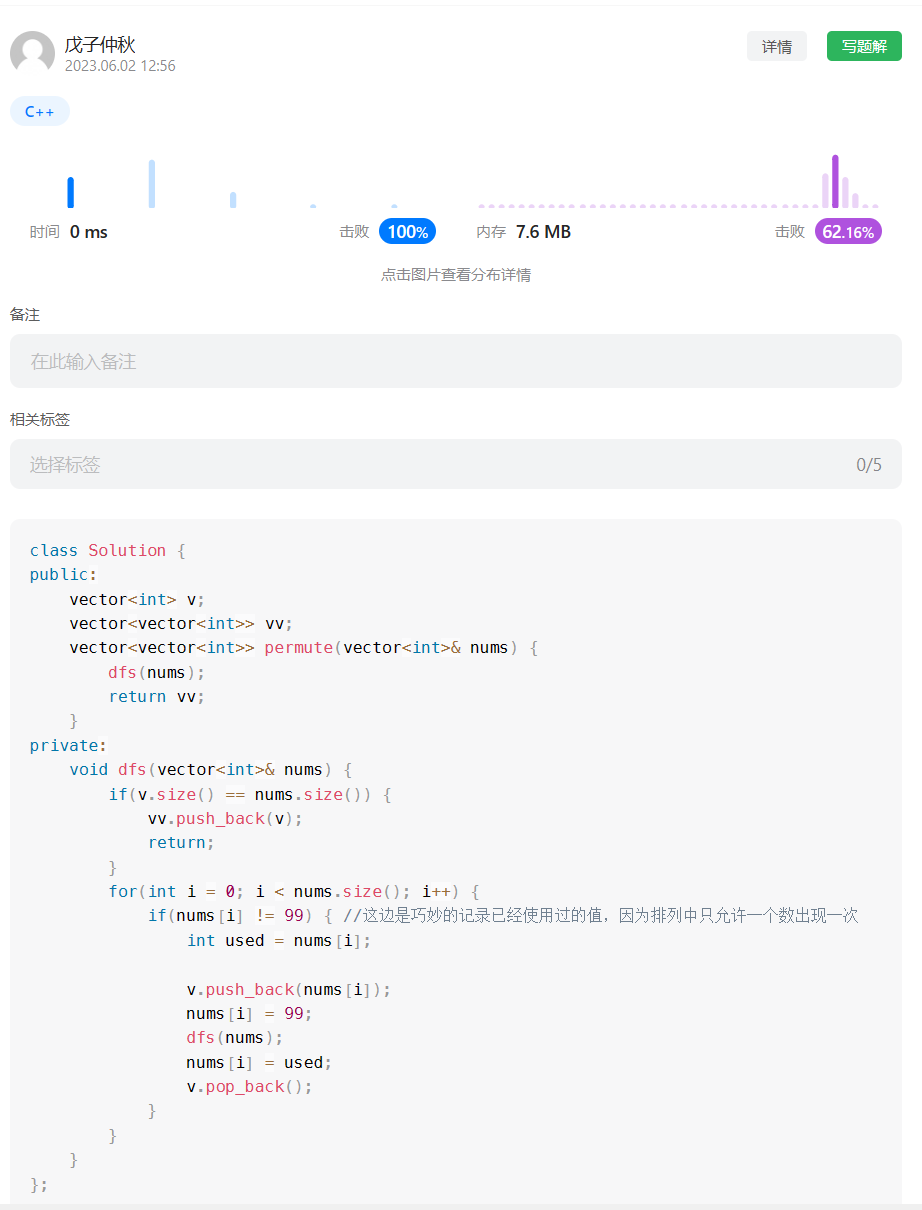
3.代码实现

class Solution {
    /**
     *哈希表法
     *时间复杂度：O(n)
     *空间复杂度：O(n)
     */
    public int[] twoSum(int[] nums, int target) {
        int[] result = new int[2];
        if(nums == null || nums.length == 0){
           return result;
        }
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0;i<nums.length;i++){
            //遍历当前元素，并在map中寻找是否有匹配的key
            int temp = target - nums[i];
            if (map.containsKey(temp)){
                result[1] = i;
                result[0] = map.get(temp);
                break;
            }else {
                map.put(nums[i],i);
            }
        }
        return result;
    }
}