一、过拟合和欠拟合

1，欠拟合
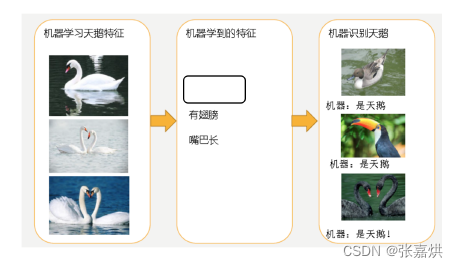
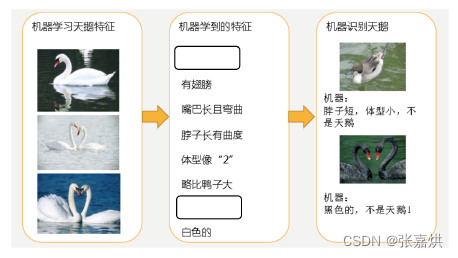
如下所示，机器学习到的天鹅特征太少了，导致区分标准太粗糙，不能准确识别出天鹅。

2，过拟合
已有的天鹅图片全是白天鹅的，机器学习认为天鹅的羽毛都是白的，在识别羽毛是黑的天鹅就会认为那不是天鹅。

总结：

• 欠拟合是因为学习数据的特征过少，解决办法是增加数据的特征数量。
• 过拟合的原因是原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点。解决方法是在机器学习的时候尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化。

二、正则化类别

• L2正则化
  作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
  优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象

• L1正则化
  作用：可以使得其中一些W的值直接为0，删除这个特征的影响

三、岭回归

岭回归，其实是一种带有 L2 正则化的线性回归。在算法建立回归方程的时候，加上正则化的限制，从而达到解决过拟合的效果

# 具有l2正则化的线性回归 API
# alpha：正则化力度λ，λ取值：0~1 1~10
# solver：会根据数据自动选择优化方法
# sag：如果数据集、特征都比较大，选择该随机梯度下降优化
# normalize：数据是否进行标准化，normalize = False 时可以在fit之前调用 StandardScaler 标准化数据
# Ridge.coef_：回归权重
# Ridge.intercept_：回归偏置
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)

四、实操：波士顿房价预测

import sklearn.datasets
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

# 获取数据
lb = sklearn.datasets.load_boston()

# 对数据集进行划分
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.3, random_state=24)

rd = Ridge(alpha=1.0)

# 模型训练
rd.fit(x_train, y_train)

# 模型预测
y_rd_predict = rd.predict(x_test)

print("岭回归的权重参数为：", rd.coef_)
print("岭回归的预测的结果为：", y_rd_predict)
print("岭回归的均方误差为：", mean_squared_error(y_test, y_rd_predict))