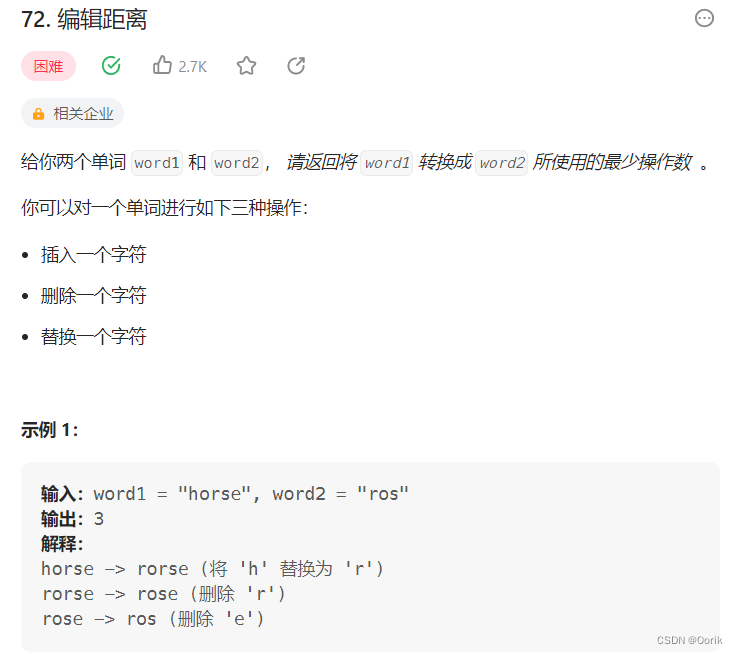
最近在写dp问题的时候，写到这个经典题，对于里面三个转换方程没太懂，偶然在评论区找到一个非常非常清楚的解释，顺便就把这道题记录一下，加上自己的理解，方便日后查看!

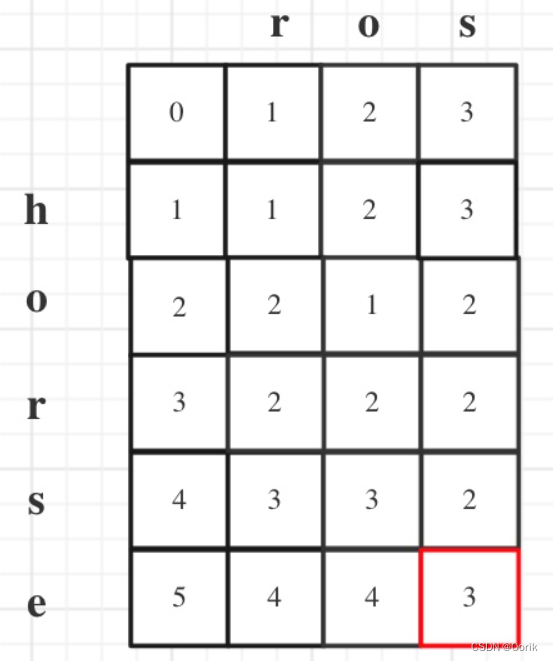
 对于这一类的dp习惯性的都初始化dp的大小为要求size的+1，因为这样方便处理0位置，去进行初始化，后面遍历的时候从1开始遍历就行。

下面写写自己的理解和总结

• dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
• 确定递推公式，有两种情况，当两个字符一样时和不一样时
• 一样时就说明不需要进行操作改变，沿用前一组的结果就行dp[i][j]=dp[i-1][j-1]
• 不一样的时候，需要进行 增 删 改三种操作

下面copy一下大佬的解释

对“dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。”的补充理解：

以 word1 为 "horse"，word2 为 "ros"，且 dp[5][3] 为例，即要将 word1的前 5 个字符转换为 word2的前 3 个字符，也就是将 horse 转换为 ros，因此有：

(1) dp[i-1][j-1]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 2 个字符 ro，然后将第五个字符 word1[4]（因为下标基数以 0 开始） 由 e 替换为 s（即替换为 word2 的第三个字符，word2[2]）

(2) dp[i][j-1]，即先将 word1 的前 5 个字符 horse 转换为 word2 的前 2 个字符 ro，然后在末尾补充一个 s，即插入操作

(3) dp[i-1][j]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 3 个字符 ros，然后删除 word1 的第 5 个字符

照着图看一下三种操作

三种操作get到了之后取最小的一个，编辑次数+1就行

• 还有初始化问题，多初始化一位就相当于前面多了个空串，也是方便写代码
• 如果 word1不空，word2空，那么1变2就要根据1有多少个去变多少次
• 同理 1空，2不空，1变2需要根据2有多少个，去变多少次

代码示例：

 int minDistance(string word1, string word2) 
{
    vector<vector<int>>dp(word1.size()+1,vector<int>(word2.size()+1));
    for(int i=0;i<=word1.size();++i)//word2是空串
    {
        dp[i][0]=i;
    }
    for(int j=0;j<=word2.size();++j)//word1是空窜
    {
        dp[0][j]=j;
    }
    for(int i=1;i<=word1.size();++i)
    {
        for(int j=1;j<=word2.size();++j)
        {
            if(word1[i-1]==word2[j-1])//相等的话，就用变了
            {
                dp[i][j]=dp[i-1][j-1];
            }
            else//不相等了 三种转变，增删改，最小的一个
            {
                dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;//加一操作统一提出放最后了
            }
        }
    }
    return dp[word1.size()][word2.size()];

  }

好忙好忙好忙·