微积分是高等数学的核心，包含微分和积分。前面几篇我们介绍了微分及其逆运算——不定积分（严格来说，不定积分属于微分模块）。

传送门：微分与导数  不定积分

今天开始，我们进入积分模块。还是老样子，先从例子开始。

1

利用初等数学可以求出一般规则图形的面积，比如圆，正多边形等。如果要求曲线围成的面积，就需要用到高等数学的思想。比如下面一个例子：要求抛物线与x轴围成的面积(0<x<1)，用初等数学显然无解。

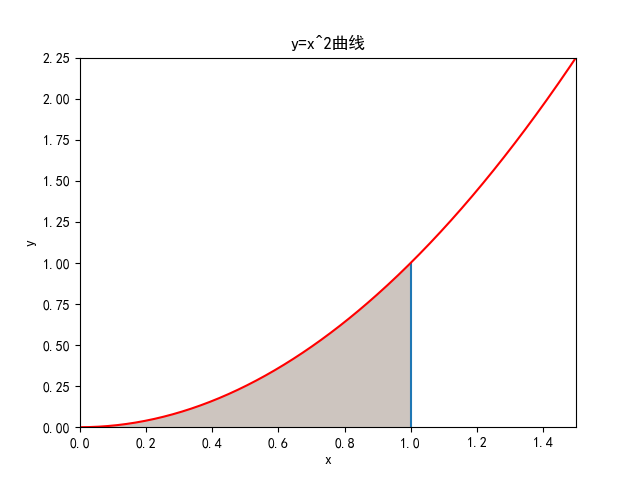
我们要利用“穷竭法”思想来解决这个问题。在区间[0,1]上等分n个点，每相邻两点的距离为h:

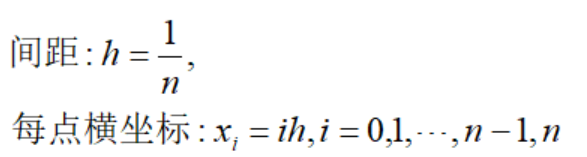
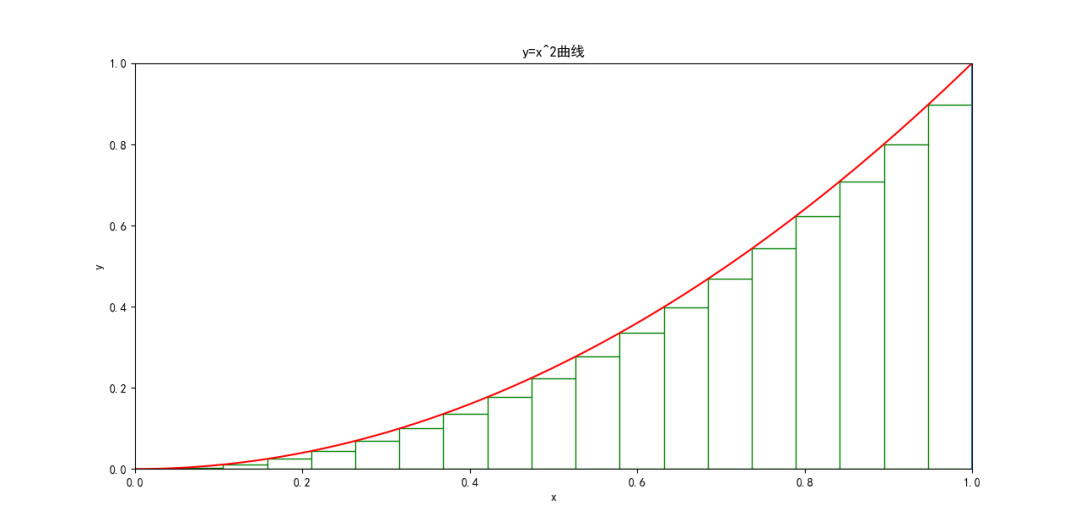
对于两两相邻的划分点，我们可以得到两个矩形——绿色部分和黄色部分（如下图的一个示例）：

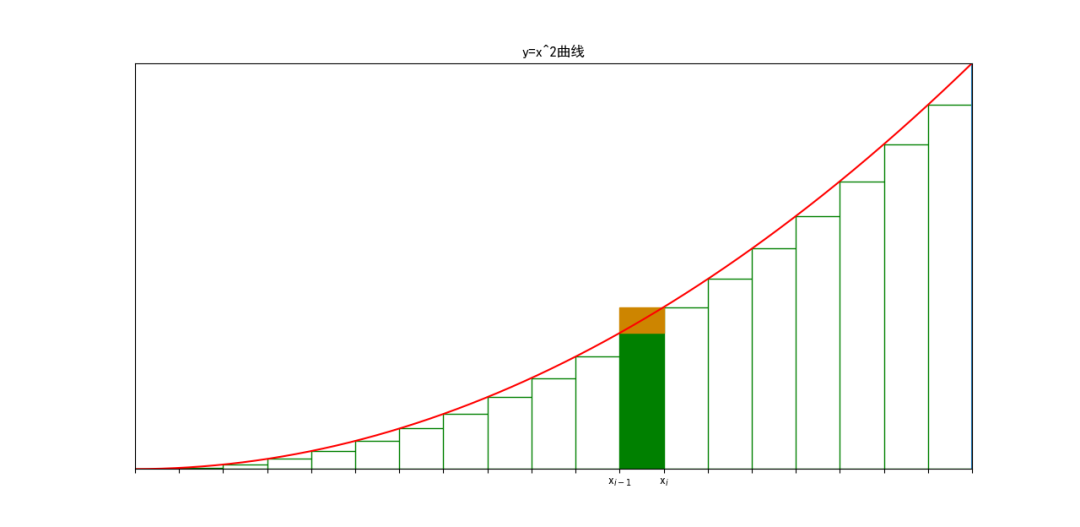
则所求面积有如下关系：

由数学归纳法，我们有：

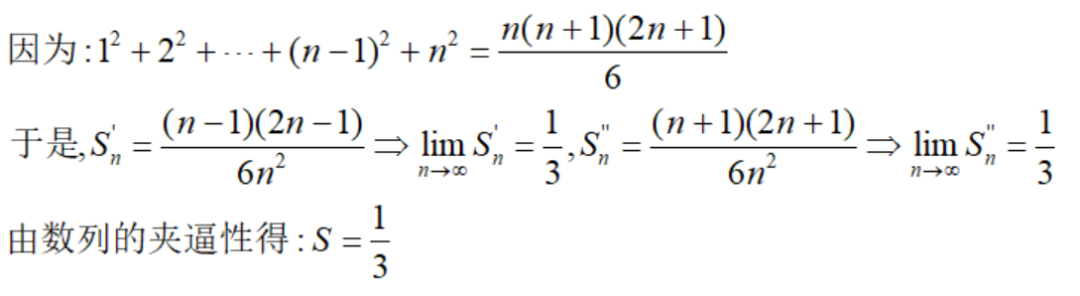
这样我们就求得了所求图形的面积。注意到，我们在两个相邻划分点中间任取一点ξ，则可以构成蓝色+绿色部分面积：

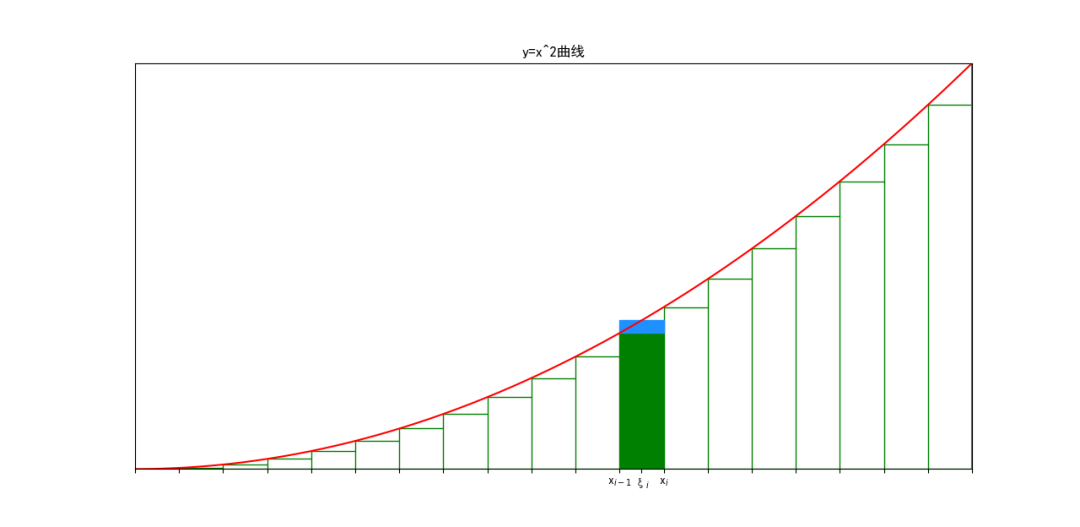
同样的我们有：

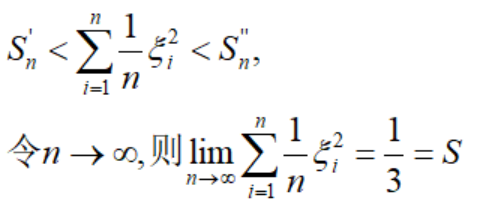
根据此，我们可以推广到另一种思路求面积：区间的分段不再是等分，只要我们将相邻两个划分点的最大间距趋于0，也可以保证其极限与图形面积相等。因此：

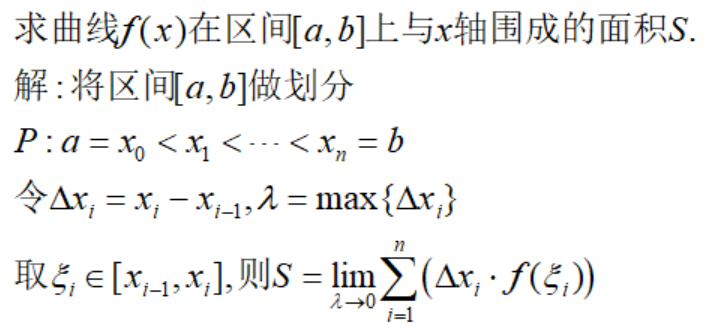
这种思想不仅可以用于求不规则图形的面积，还可以应用到别的领域，比如求变速运动的路程：

2

由此我们引出定积分的定义：

根据定义，我们立马有结论：

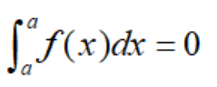
定积分是一种函数极限，因此也有“ε-δ”语言：

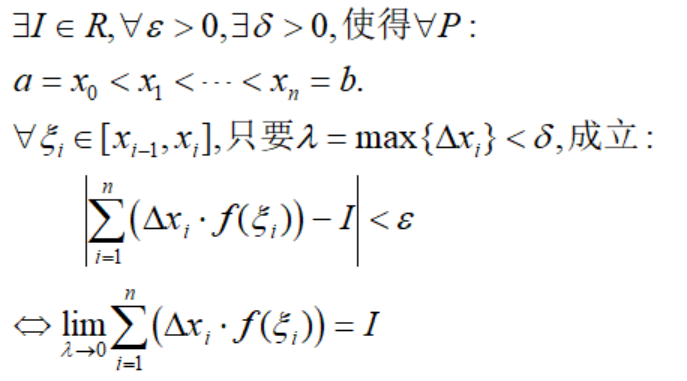
下面举个例子，证明狄利克雷函数不可积。

3

接下来我们探讨黎曼可积的充分必要条件，为此，要介绍达布定理，而在此之前，得先引入达布和概念以及相关的两个引理。

下面介绍Darboux和（达布和）概念：

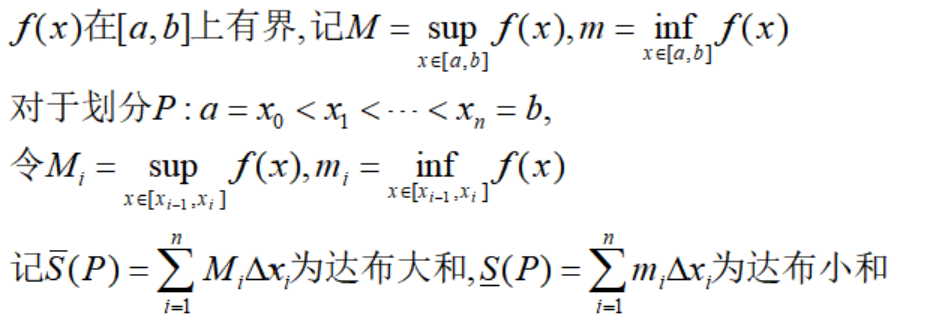
根据确界的定义，显然有下面不等式成立：

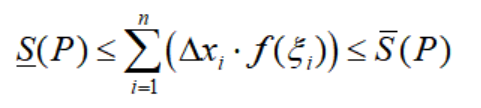
引入两个引理。

引理1：若在原划分中增加一个分点，则大和不增，小和不减

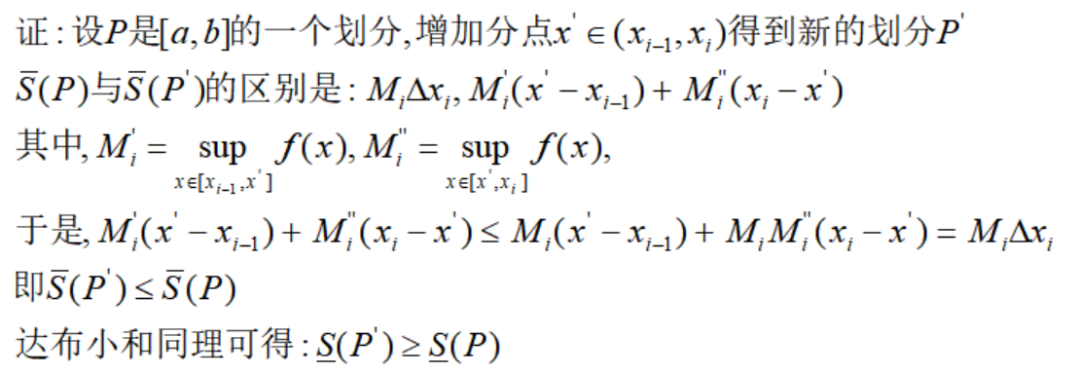
引理2：对任意的两个划分，一个划分的达布大和必定大于等于另一个划分的达布小和

根据引理2，把任意划分的达布大和作为一个集合，任意划分的达布小和作为另一个集合，它们都是有界的，所以确界存在，可以推出下面的关系：

下面我们可以来证明达布定理：

这里要说明三点，第一点是倒数第二行的不等式。一共三部分，蓝色部分根据证明的第一行显然是小于ε/2；黄色部分根据引理1可知其差值必小于等于0，绿色部分可以这样理解：

最后一个不等式小编再展开做了详细推导，只需要看一个小区间的就行：

关于达布定理要说明的第二点是证明的红色部分，它正是满足函数“ε-δ”语言，因此极限被证明。

第三点是最重要的一点，从达布定理证明的过程，我们可以知道，最终能够证明结论的逻辑是：

4

有了达布定理，我们可以来看黎曼可积的充要条件了，有定理：

用文字描述就是：黎曼可积的充要条件是任意划分P下的达布大和与达布小和极限相等

函数在某一区间的最大值与最小值的差值表示了振幅，那么黎曼可积的充要条件可以有第二种表达形式：

根据这个定理我们再来看狄利克雷函数不可积是非常简单的：

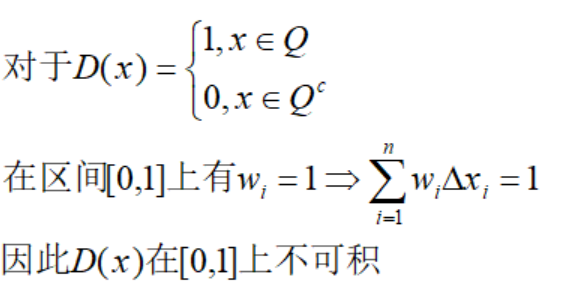
推论1：闭区间上的连续函数一定可积

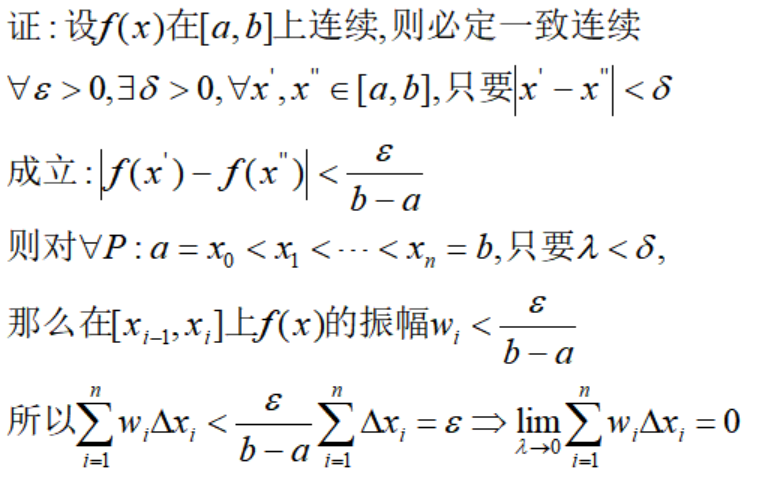
推论2：闭区间上的单调函数必定可积

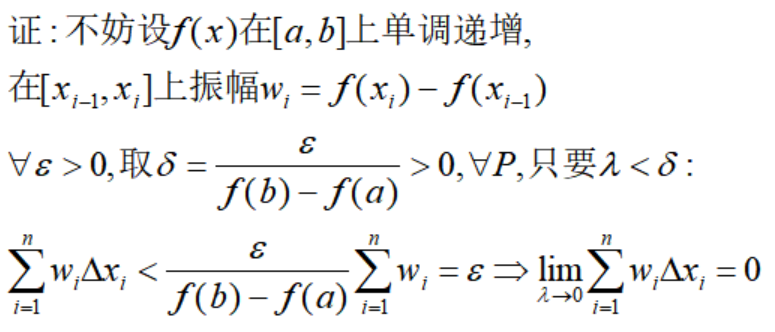
回忆达布定理证明的第三点，我们还能给出黎曼可积充要条件的第三种表达形式：

利用达布定理要注意的第三点可以完成证明，这里不再展开。而从这个等价条件我们可以得到第三条推论。

推论3：闭区间上只有有限个不连续点的有界函数一定可积

如果有多个但有限不连续点，按照上面方法不断划分即可证明.

现在我们可以证明黎曼函数可积。回顾一下黎曼函数，它是以1为周期的函数：

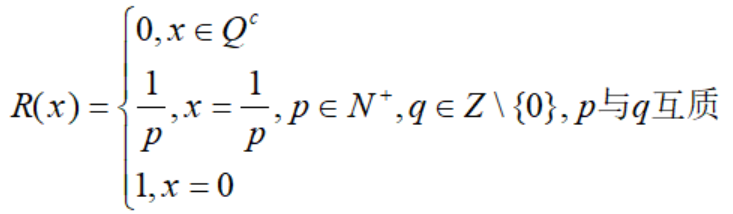
传送门:连续函数

附录：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


x = np.linspace(0,1,500)
y = x**2
x_bar = np.linspace(0,1,20)
y_bar = x_bar**2


color = ['white' if i != 11 else 'green' for i in range(20)]
x_label = []
for i in range(20):
    if i == 11:
        x_label.append('x$_{i-1}$')
    elif i == 12:
        x_label.append('x$_{i}$')
        # x_label.append('ξ$_{i}$')
    else:
        x_label.append('')


fig,ax = plt.subplots()
plt.vlines(1,0,1)
plt.plot(x, y, c='r',label='x**2')
plt.bar(x_bar, y_bar, color=color, edgecolor='green',width=0.5,align='edge')  # 绘制y刻度标签
ax.add_patch(patches.Rectangle((x_bar[11], y_bar[11]),x_bar[12]-x_bar[11],y_bar[12]-y_bar[11],edgecolor='#CD8500',facecolor='#CD8500',fill=True))
# ax.add_patch(patches.Rectangle((x_bar[11], y_bar[11]),x_bar[12]-x_bar[11],(y_bar[12]-y_bar[11])/2,edgecolor='#1E90FF',facecolor='#1E90FF',fill=True))
plt.xlim(0, 1)
plt.ylim(0, 1)
# x_bar = list(x_bar)
# x_bar.insert(11,(x_bar[11]+x_bar[12])/2)
# x_label.insert(11,'ξ$_{i}$')
plt.xticks(x_bar, x_label)  # 绘制x刻度标签
plt.yticks([])
plt.title("y=x^2曲线")
plt.show()