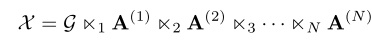1.蒙特卡洛
基本流程
蒙特卡洛模拟法基于随机抽样原理,通过生成大量的随机样本,从而对目标变量进行估计和分析。具体来说,蒙特卡洛模拟法的基本流程如下:
1.确定问题:首先需要明确要解决的问题是什么,以及需要估计或求解的目标是什么。
2.建立模型:需要建立一个适当的数学模型来描述问题。
3.生成随机样本:根据问题的模型,使用合适的随机抽样方法生成随机样本。
4.计算目标函数:对于每个生成的随机样本,根据问题的定义计算目标函数的值。
5.统计分析:对计算得到的目标函数值进行统计分析,可能包括计算均值、方差、置信
区间、概率分布等。通过统计分析可以获得对问题的估计值或近似解。
6.收敛性检验:在得到一定数量的随机样本后,需要进行收敛性检验,以确定结果的稳
定性和准确性。
7.结果解释和应用:根据具体问题,解释和应用蒙特卡洛方法得到的结果。
优点
适用性广泛:蒙特卡洛方法可以应用于各种不同的问题领域,包括数值计算、概率统计、优化问题等。它的灵活性使其可以解决那些难以用传统解析方法求解的复杂问题。
相对简单:蒙特卡洛方法的实现相对简单,特别是与其他数值方法相比。它通常只需要生成随机样本,并进行简单的统计分析,而不需要推导复杂的数学公式或求解高阶方程。
可并行化处理:由于蒙特卡洛方法的计算步骤相互独立,可以将问题分解成多个子问题并进行并行计算。这使得蒙特卡洛方法在并行计算环境中具有较好的可扩展性和高效性。
提供不确定性量化:蒙特卡洛方法能够量化问题中的不确定性,并提供关于结果的概率分布或置信区间。这使得决策者可以更好地了解风险和不确定性,并做出相应的决策。
缺点
高计算成本:蒙特卡洛方法通常需要生成大量的随机样本来获得准确的结果。随着问题的复杂性和维度的增加,计算成本呈指数级增长。这可能需要大量的计算资源和时间。
收敛速度慢:蒙特卡洛方法的收敛速度通常较慢。尤其是对于问题空间中的高维度问题,需要生成的随机样本数量很大才能获得满意的结果。这可能导致计算时间较长。
随机误差:蒙特卡洛方法的结果受到随机抽样的影响,因此存在随机误差。即使使用大量的样本,结果也可能存在一定的偏差。这需要通过收敛性检验和统计分析来评估结果的可靠性。
不适用于某些问题:蒙特卡洛方法并不适用于所有类型的问题。对于某些问题,特别是具有高度结构化和规则性的问题,可能存在更有效的解析方法或数值方法。
举例
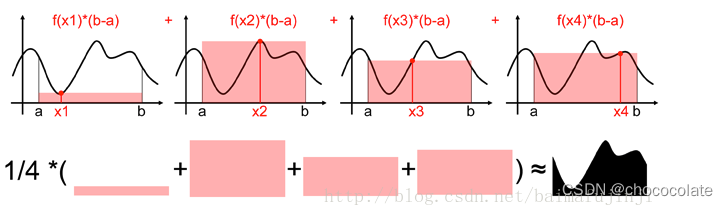
计算[a,b]的积分。
我们在[a,b]之间随机取一系列点xi,然后把估算出来的面积取平均来作为积分估计的近似值。采样点越多,对这个积分的估计也就越来越接近。
2.广义多项式
正交多项式是一类特殊的多项式函数,它们在某种权重函数的内积下是正交的。这些多项式函数与许多概率分布密切相关,并且在概率统计中起着重要的作用。
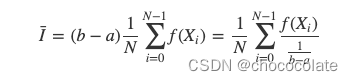




![[Daimayuan] 模拟输出受限制的双端队列(C++,模拟)](https://img-blog.csdnimg.cn/img_convert/c579fddf4fe58f965959dc262fc69109.png)