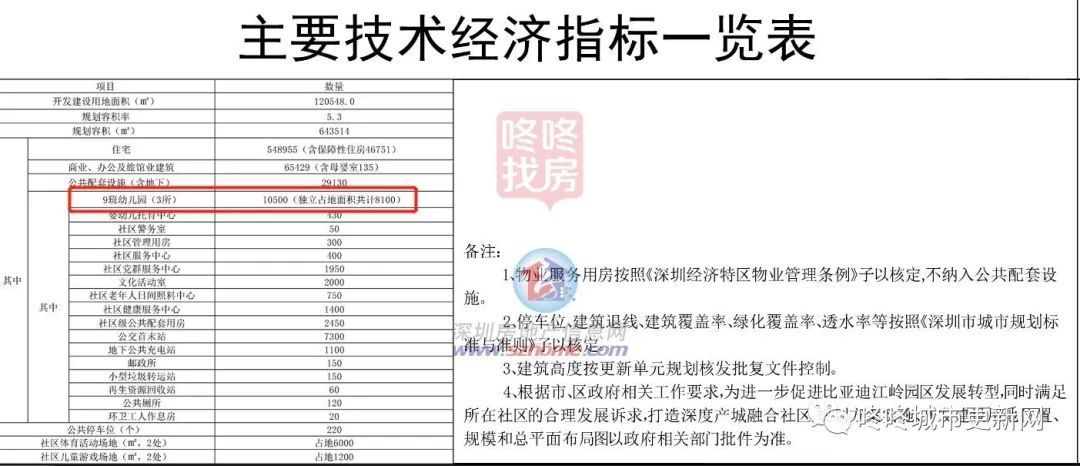
文章目录
- 卷积编码
- 维特比译码
卷积编码
卷积码是一种非分组码,通常适用于前向纠错。在分组码中,编码器产生的 n 个码元的一个码组,完全决定于这段时间中 k 比特输入信息。这个码组中的监督位仅监督本码组中 k 个信息位。卷积码在编码时虽然也是把 k 比特的信息段编成 n 个比特的码组,但是监督码元不仅和当前的 k 比特信息段有关,而且还同前面 m = (N -1) 个信息段有关,所以一个码组中的监督码元监督着N个信息段。通常将 N 称为编码约束度,并将 nN 称为编码约束长度。
一般说来,对于卷积码,k 和 n 的值是比较小的整数,且 n 大于 k,将卷积码记作 (n,k,N),码率定义为
k
n
\frac{k}{n}
nk。
编码器由三种主要的元件构成,包括 Nk 级移存器,n 个模2加法器和一个旋转开关。每个模2加法器的输入端数目可以不同,它连接到一些移存器的输出端,模2加法器的输出端接到旋转开关上,旋转开关每时隙旋转一周,输出 n 比特。将时间分成等间隔的时隙,在每个时隙中有 k 比特从左端进入移存器,并且移存器各级暂存的信息向右移 k 位。
卷积编码器一般原理方框图如下图所示。

一种 (3,1,3) 卷积编码器的方框图如下图所示。

根据上面方框图有:
c
i
=
b
i
{c_i}={b_i}
ci=bi
d
i
=
b
i
⊕
b
i
−
2
{d_i}={b_i}⊕{b_{i-2}}
di=bi⊕bi−2
e
i
=
b
i
⊕
b
i
−
1
⊕
b
i
−
2
{e_i}={b_i}⊕{b_{i-1}}⊕{b_{i-2}}
ei=bi⊕bi−1⊕bi−2
其中,
b
i
{b_i}
bi为当前输入的信息位,
b
i
−
1
{b_{i-1}}
bi−1和
b
i
−
2
{b_{i-2}}
bi−2为移存器存储的前两位信息。
根据
M
3
M
2
{M_3M_2}
M3M2的不同,定义的状态表如下。
| M 3 M 2 {M_3M_2} M3M2 | 对应的状态 |
|---|---|
| 00 | a |
| 01 | b |
| 10 | c |
| 11 | d |
移存器状态和输入输出码元的关系如下表所示。
| 移存器前一状态 M 3 M 2 {M_3M_2} M3M2 | 输入 b i {b_i} bi | M 3 M 2 M 1 {M_3M_2M_1} M3M2M1 | c i d i e i {c_id_ie_i} cidiei | 移存器下一状态 M 3 M 2 {M_3M_2} M3M2 |
|---|---|---|---|---|
| a(00) | b 1 = 0 {b_1}=0 b1=0 | 000 | 000 | a(00) |
| a(00) | b 1 = 1 {b_1}=1 b1=1 | 001 | 111 | b(01) |
| b(01) | b 2 = 0 {b_2}=0 b2=0 | 010 | 001 | c(10) |
| b(01) | b 2 = 1 {b_2}=1 b2=1 | 011 | 110 | d(11) |
| c(10) | b 3 = 0 {b_3}=0 b3=0 | 100 | 011 | a(00) |
| c(10) | b 3 = 1 {b_3}=1 b3=1 | 101 | 100 | b(01) |
| d(11) | b 4 = 0 {b_4}=0 b4=0 | 110 | 010 | c(10) |
| d(11) | b 4 = 1 {b_4}=1 b4=1 | 111 | 101 | d(11) |
可以看到,状态a的下一状态只能是a或b,状态b的下一状态只能是c或d,状态c的下一状态只能是a或b,状态d的下一状态只能是c或d。
卷积码的几何表述可以分为码树图、状态图和网格图。
上面 (3,1,3) 卷积编码器对应的码树图如下图所示。

在码树图中,输入信息位为0,则状态向上移动,输入信息位为1,则状态向下移动。
可以看到,从第四级支路开始,码树的上半部和下半部相同,这意味着从第四个输入信息位开始,输出码元已经与第一位输入信息无关,即此编码器的约束度 N=3。而且在码树图上,通过输入信息位很容易读出编码之后的输出序列,比如输入序列为:1101,则输出序列为:111 110 010 100。读的时候,输入信息位为1则读下面支路,输入信息位为0则读上面的支路。
上面 (3,1,3) 卷积编码器对应的状态图如下图所示。

在状态图中,虚线表示输入信息位为1时状态转变的路线,实线表示输入信息位为0时状态转变的路线。
线条旁边的3位数字是编码输出比特,利用状态图也可以很容易的根据输入序列得到输出序列。读取的时候从a状态开始,输入为1读虚线上的3位作为输出,输入为0读实线上的3位作为输出,然后跳到下一状态接着读取。
上面 (3,1,3) 卷积编码器对应的网格图如下图所示。

在网格图中,虚线表示输入信息位为1,实线表示输入信息位为0。
可以看到,在第4时隙以后的网格图形完全是重复第3时隙的图形,这也反映了该卷积码的约束长度为 3。
维特比译码
维特比译码算法是维特比在1967年提出的,这种方法比较简单,计算快,故得到了广泛的应用。基本原理是:将接收到的信号序列和所有可能的发送信号序列比较,选择其中汉明距离最小的序列认为是当前发送信号序列。
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。如0000和1111的汉明距离是4,0000和0101的汉明距离是2。
下面通过这个例子来说明维特比译码过程,假设发送的序列为 1101,编码之后的序列为 111 110 010 100。
由于这是一个 (n,k,N) = (3,1,3) 卷积码,发送序列的约束度 N = 3,所以首先要考察前 nN = 9 位,即 111 110 010,沿路径每一级有4种状态,每种状态只有两条路径可以到达,故4种状态共有8条到达路径,现在比较这8条路径的对应序列和接收序列 111 110 010 之间的汉明距离,列表如下。
| 路径 | 对应序列 | 汉明距离 | 幸存与否 |
|---|---|---|---|
| aaaa | 000 000 000 | 6 | 否 |
| abca | 111 001 011 | 4 | 是 |
| aaab | 000 000 111 | 7 | 否 |
| abcb | 111 001 100 | 5 | 是 |
| aabc | 000 111 001 | 6 | 否 |
| abdc | 111 110 010 | 0 | 是 |
| aabd | 000 111 110 | 5 | 否 |
| abdd | 111 110 101 | 3 | 是 |
将到达每个状态的两条路径的汉明距离作比较,将距离小的一条路径保留,称为幸存路径(surviving path)。若两条路径的汉明距离相同,则可以保留任意一条,这样就只剩下4条路径。
接下来继续考察后继三位100,计算上述四条幸存路径增加一级后的8条可能路径的汉明距离,如下表所示。
| 路径 | 原幸存路径的汉明距离 | 新增路径 | 新增距离 | 总距离 | 幸存与否 |
|---|---|---|---|---|---|
| abca+a | 4 | aa(000) | 1 | 5 | 否 |
| abdc+a | 0 | ca(011) | 3 | 3 | 是 |
| abca+b | 4 | ab(111) | 2 | 6 | 否 |
| abdc+b | 0 | cb(100) | 0 | 0 | 是 |
| abcb+c | 5 | bc(001) | 2 | 7 | 否 |
| abdd+c | 3 | dc(010) | 2 | 5 | 是 |
| abcb+d | 5 | bd(110) | 1 | 6 | 否 |
| abdd+d | 3 | dd(101) | 1 | 4 | 是 |
表中最小的汉明距离是0,对应的路径是abdcb,其对应的序列是 111 110 010 100,与输入的编码序列一致,故其对应的发送序列就是 1101,至此完成了译码。
如果序列中有少量的比特错误,也是可以完成译码的。
还是上面的这个例子,发送的序列为 1101,编码之后的序列为 111 110 010 100,假设接收到的序列中第4位和第11位发生了错误,即收到的序列为 111 010 010 110。
同样的方法列表分析,先考察前 nN = 9 位 111 010 010,比较8条路径的对应序列和接收序列 111 010 010 之间的汉明距离,列表如下。
| 路径 | 对应序列 | 汉明距离 | 幸存与否 |
|---|---|---|---|
| aaaa | 000 000 000 | 5 | 否 |
| abca | 111 001 011 | 3 | 是 |
| aaab | 000 000 111 | 6 | 否 |
| abcb | 111 001 100 | 4 | 是 |
| aabc | 000 111 001 | 7 | 否 |
| abdc | 111 110 010 | 1 | 是 |
| aabd | 000 111 110 | 6 | 否 |
| abdd | 111 110 101 | 4 | 是 |
接下来继续考察后继三位110,计算上述四条幸存路径增加一级后的8条可能路径的汉明距离,如下表所示。
| 路径 | 原幸存路径的汉明距离 | 新增路径 | 新增距离 | 总距离 | 幸存与否 |
|---|---|---|---|---|---|
| abca+a | 3 | aa(000) | 2 | 5 | 否 |
| abdc+a | 1 | ca(011) | 2 | 3 | 是 |
| abca+b | 3 | ab(111) | 1 | 4 | 否 |
| abdc+b | 1 | cb(100) | 1 | 2 | 是 |
| abcb+c | 4 | bc(001) | 3 | 7 | 否 |
| abdd+c | 4 | dc(010) | 1 | 5 | 是 |
| abcb+d | 4 | bd(110) | 0 | 4 | 是 |
| abdd+d | 4 | dd(101) | 2 | 6 | 否 |
表中最小的汉明距离是2,对应的路径仍然是abdcb,其对应的序列是 111 110 010 100,与输入的编码序列一致,故其对应的发送序列就是 1101,至此也完成了正确的译码。
以上就是卷积编码和维特比译码的所有内容了!
本文参考资料:
通信原理 / 樊昌信,曹丽娜编著