说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

Day61 决策树

结合老师的文章去理解决策树中的一种决策算法：ID3算法

1.什么是决策树

决策树是一种基于树型结构的机器学习算法，叶子结点表示一个类别（即预测值），非叶结点表示特征。这篇文章构建决策树采用的是ID3算法，主要是根据信息增益（或条件信息熵）来划分特征。

2.什么是熵

在决策树中，熵是一种衡量数据集纯度或混乱度的指标。熵的值越高，表示数据集的混乱程度越高; 熵的值越低，表示数据集的纯度越高。（具体知识可网上查阅）

熵计算公式：
$H(X)=-\sum_{i}^{n}p(x_{i})logp(x_{i})$
条件熵的计算公式
$H(Y|X)=-\sum_{i}^{n}p(x)H(Y|X=x)$

3.什么是信息增益

熵是衡量数据集的不确定性的度量，而条件熵是在已知某个属性的条件下，数据集的不确定性。信息增益表示使用某个特征进行划分后，整个数据集的熵减少的程度，即通过划分所获得的信息量。信息增益越大，表示使用特征 $A$ 进行划分后，数据集的确定性更高，特征A对训练数据集D的信息增益g(D, A) （具体知识可网上查阅）
$g (D, A) = H (D) - H (D ∣ A)$

4.详细例子

这个例子计算主要是结合了文章中的代码思路来的。

1. weather样本

在这里插入图片描述

2.第一次决策

计算每个特征值的条件熵,筛选最优的特征作为根结点。
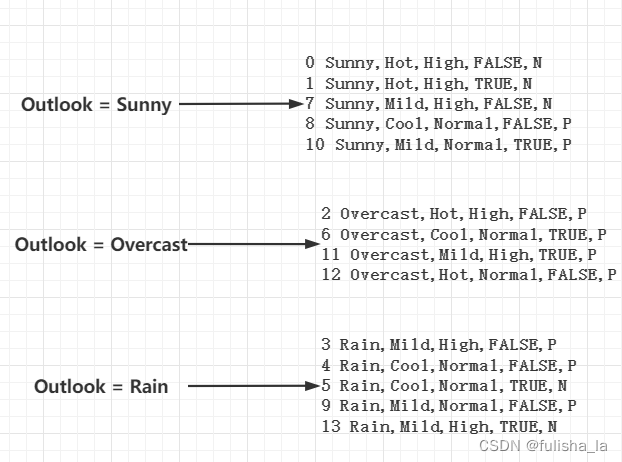
在这里插入图片描述
计算Outlook 他每个属性的熵：
$Sunny)=-\frac{3}{5}\log \frac{3}{5}-\frac{2}{5}\log \frac{2}{5}=0.6730$
$Overcast)=-0\log 0-1\log1=0.0$
$Rain)=-\frac{2}{5}\log \frac{2}{5}-\frac{3}{5}\log \frac{3}{5}=0.6730$
计算Outlook 的条件熵：
$H(play|Outlook)=-\frac{5}{14}*0.6730 -\frac{4}{14}*0.0-\frac{5}{14}*0.6730 = 0.4807$

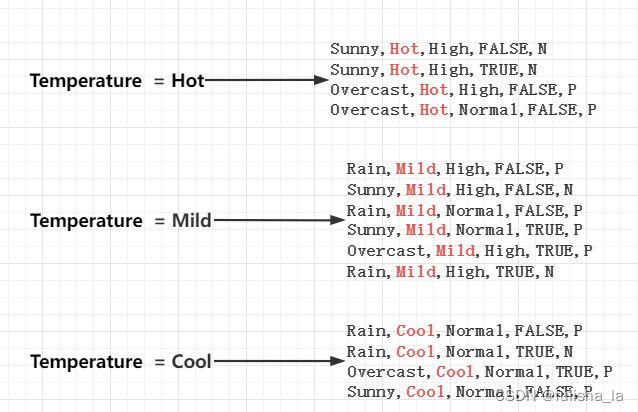
在这里插入图片描述
计算Temperature他每个属性的熵：
$Hot)=-\frac{2}{4}\log \frac{2}{4}-\frac{2}{4}\log \frac{2}{4}=0.6931$
$Mild)=-\frac{2}{6}\log \frac{2}{6}-\frac{4}{6}\log \frac{4}{6}=0.6365$
$Cool)=-\frac{1}{4}\log \frac{1}{4}-\frac{3}{4}\log \frac{3}{4}=0.5623$
计算Temperature的条件熵：
$H(play|Temperature)=-\frac{4}{14}*0.6730 -\frac{6}{14}*0.0-\frac{4}{14}*0.6730 = 0.6315$
同理可得Humidity和Windy的条件熵：
$H (pl a y ∣ H u mi d i t y) = 0.5465$
$H (pl a y ∣ Win d y) = 0.6183$
所以在第一轮的决策中，我们根据最大化信息增益, 与最小化条件信息熵，选择条件熵最小的Outlook作为决策的根结点进行分裂。
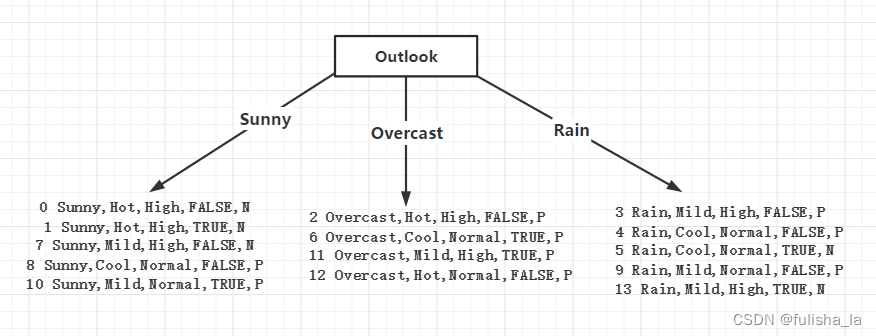
在这里插入图片描述

3.第二次决策

我们在第一次决策后，分了三个分支，他的子问题和原问题一样的，又进行递归建树。

Outlook-Sunny结点
- Temperature
  $Hot)=-0\log 0-1\log 1=0.0$
  $Mild)=-\frac{1}{2}\log \frac{1}{2}-\frac{1}{2}\log \frac{1}{2}=0.6931$
  $Cool)=-0\log 0-1\log 1=0.0$
  $H(play|Temperature)=-\frac{2}{5}*0.0 -\frac{2}{5}*0.6931-\frac{1}{5}*0.0 = 0.2772$
- Humidity
  $H (pl a y ∣ H u mi d i t y) = 0.0$
- Windy
  $H (pl a y ∣ Win d y) = 0.6591$
  选择条件熵最小的Humidity作为决策进行分裂，然后再往里面递归
Outlook-Overcast结点
在Overcast结点熵所有的play都是P,说明他的数据很纯，不用分裂了。
Outlook-Rain结点同理可得。
至于进一步的递归如上面一样

4.最终决策树

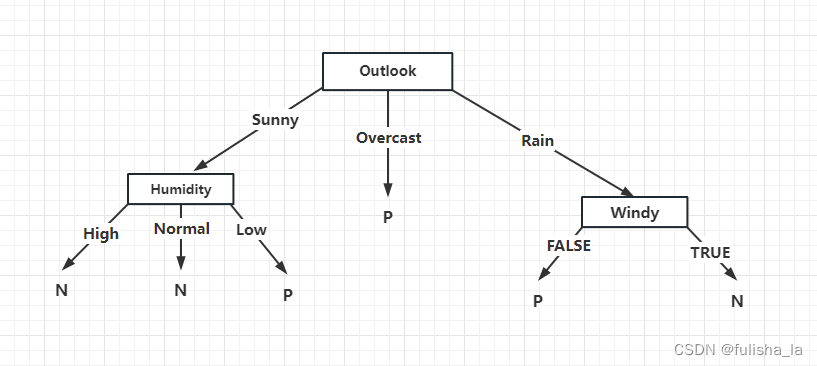
在这里插入图片描述

4. 代码理解

4.1 变量理解

在代码的实现中，很多存储都是利用的数据存储的索引，而不是存具体的数据，这样不仅减少空间开销，还减小了逻辑的复杂度。

numClasses； availableInstances； availableAttributes
通过这张图就基本可以理解这三个变量主要存储的值是那些

在这里插入图片描述

splitAttribute，ID3[] children
即每次建树时，选择那个特征值作为来进行划分子集。例如splitAttribute=0，代表选择Outlook来划分子集

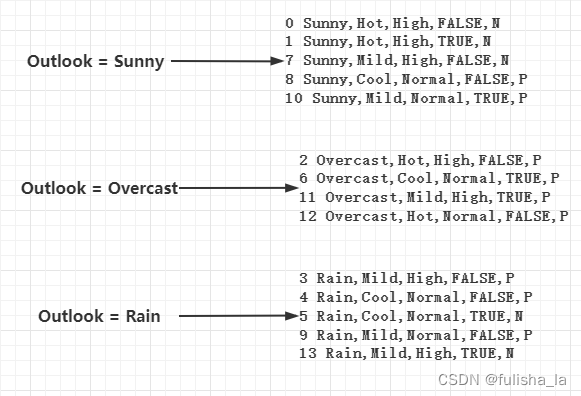
在这里插入图片描述

label
基于规定的数据集，判断数据集中出现类别最多的值赋值给lable。
如下规定的5个数据集中，N出现最多则label赋值为N的索引值。

在这里插入图片描述

4.2 代码中主要方法理解

如果能自己去手动模拟一次，代码就很好理解。如果去计算过一遍在ID3算法中，buildTree()方法是算法核心。

 public void buildTree() {
        //判断实例索引
        if (pureJudge(availableInstances)) {
            return;
        }
        if (availableInstances.length <= smallBlockThreshold) {
            return;
        }

        //划分孩子
        selectBestAttribute();
        int[][] tempSubBlocks = splitData(splitAttribute);
        children = new ID3[tempSubBlocks.length];

        // Construct the remaining attribute set.
        int[] tempRemainingAttributes = new int[availableAttributes.length - 1];
        for (int i = 0; i < availableAttributes.length; i++) {
            if (availableAttributes[i] < splitAttribute) {
                tempRemainingAttributes[i] = availableAttributes[i];
            } else if (availableAttributes[i] > splitAttribute) {
                tempRemainingAttributes[i - 1] = availableAttributes[i];
            }
        }

        // Construct children.
        for (int i = 0; i < children.length; i++) {
            if ((tempSubBlocks[i] == null) || (tempSubBlocks[i].length == 0)) {
                children[i] = null;
                continue;
            } else {
                // System.out.println("Building children #" + i + " with
                // instances " + Arrays.toString(tempSubBlocks[i]));
                children[i] = new ID3(dataset, tempSubBlocks[i], tempRemainingAttributes);

                // Important code: do this recursively
                children[i].buildTree();
            }
        }
    }

调用pureJudge方法判断他们的类别是否够纯，若类别都是一样的，则直接返回；反之跳过。
例如availableInstances目前传入的是weather样本中14个实例，很明显play有N,有P,直接跳过。

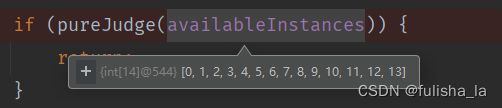
在这里插入图片描述

判断我们在建树的实例是否小于smallBlockThreshold，若小于这个树，划分出来的结果不一定好，反而会适得其反。（避免过拟合）
调用selectBestAttribute方法。这个方法就是在每次建树时选择（可选的特征值中熵最小的）。conditionalEntropy方法就是计算每个特征值的条件信息熵，具体的算法就是上面的公式。（我觉得这个方法是核心）
调用splitData方法。根据选择最小的特征值作为根结点划分子集。
buildTree方法中第一个for循环是去掉已经被选择的特征值
buildTree方法中第二个for循环是开始递归建树啦，在递归时构建ID3对象时，我们可以当作是要重新构建一颗新(子)树，传参方式有变化，是因为paraAvailableInstances， paraAvailableAttributes我们设置为成员变量，他的作用域是整个类都可用，如不更新则会导致数据出错。

 /**
     * Select the best attribute.
     * @return The best attribute index.
     */
    public int selectBestAttribute() {
        splitAttribute = -1;
        double tempMinimalEntropy = 10000;
        double tempEntropy;
        //循环遍历每个特征值，计算其条件熵
        for (int i = 0; i < availableAttributes.length; i++) {
            tempEntropy = conditionalEntropy(availableAttributes[i]);
            if (tempMinimalEntropy > tempEntropy) {
                tempMinimalEntropy = tempEntropy;
                splitAttribute = availableAttributes[i];
            }
        }
        return splitAttribute;
    }

    /**
     * Compute the conditional entropy of an attribute.
     * @param paraAttribute The given attribute
     * @return The entropy.
     */
    public double conditionalEntropy(int paraAttribute) {
        // Step 1. Statistics.
        int tempNumClasses = dataset.numClasses();
        int tempNumValues = dataset.attribute(paraAttribute).numValues();
        int tempNumInstances = availableInstances.length;
        double[] tempValueCounts = new double[tempNumValues];
        double[][] tempCountMatrix = new double[tempNumValues][tempNumClasses];

        int tempClass, tempValue;
        for (int i = 0; i < tempNumInstances; i++) {
            tempClass = (int) dataset.instance(availableInstances[i]).classValue();
            tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
            tempValueCounts[tempValue]++;
            tempCountMatrix[tempValue][tempClass]++;
        }

        // Step 2.
        double resultEntropy = 0;
        double tempEntropy, tempFraction;
        for (int i = 0; i < tempNumValues; i++) {
            if (tempValueCounts[i] == 0) {
                continue;
            }
            tempEntropy = 0;
            for (int j = 0; j < tempNumClasses; j++) {
                tempFraction = tempCountMatrix[i][j] / tempValueCounts[i];
                if (tempFraction == 0) {
                    continue;
                }
                double entropy  = -tempFraction * Math.log(tempFraction);
                tempEntropy += entropy;
            }
            double  resultEntropyTest =  tempValueCounts[i] / tempNumInstances * tempEntropy;
            resultEntropy += resultEntropyTest;
        }

        return resultEntropy;
    }

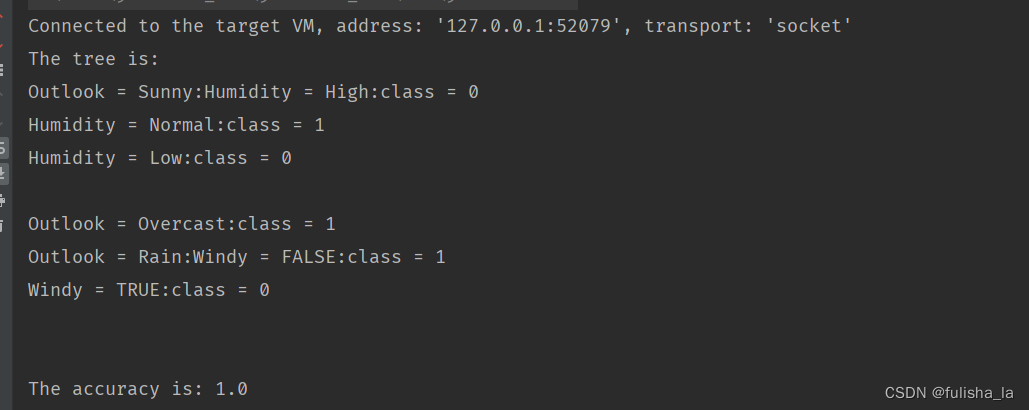
运行结果：
在这里插入图片描述