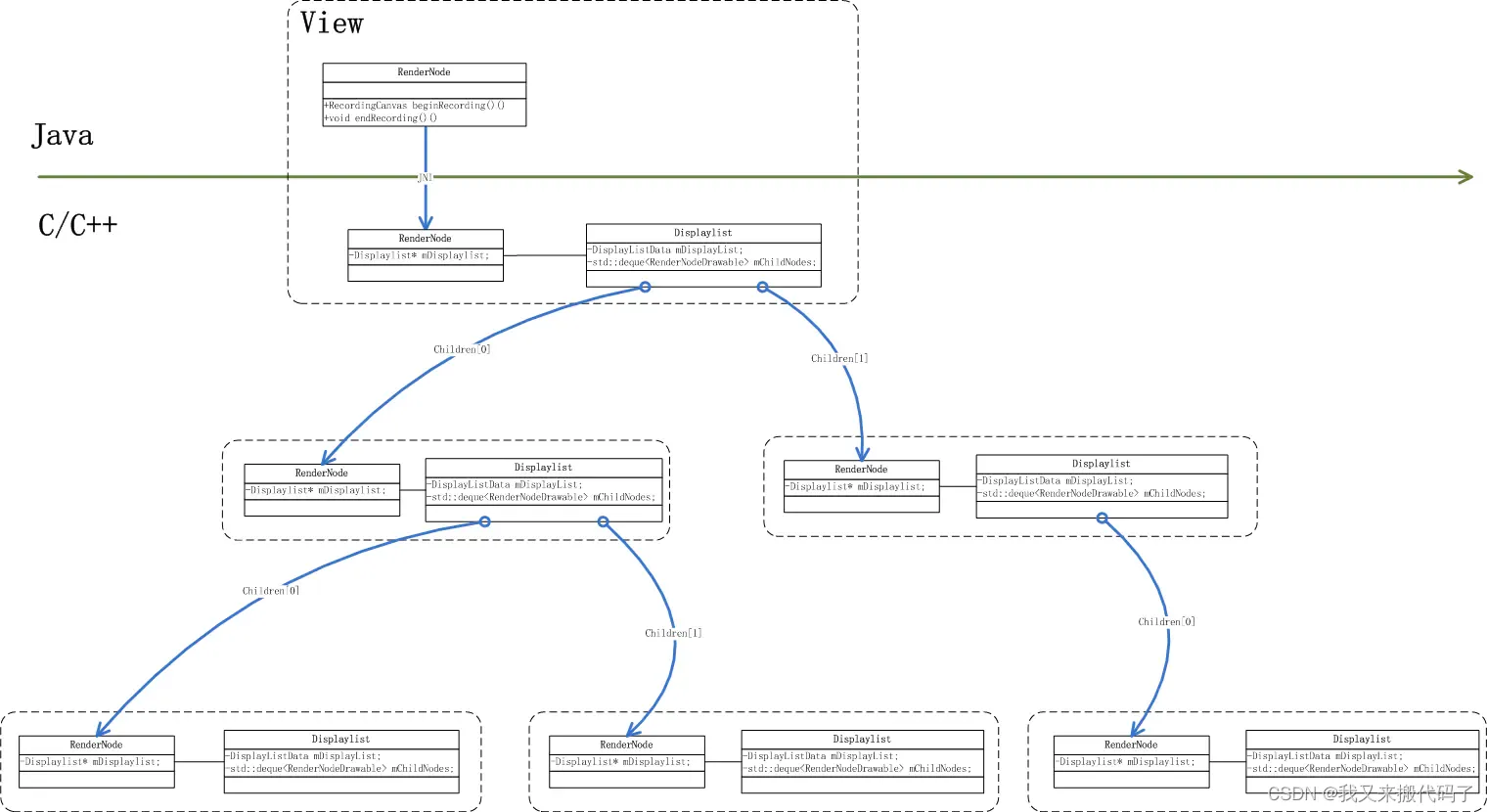
一个 恋爱关系图
胡图图love:98于小美
胡图图love:48何壮壮
胡图图love:99小怪
于小美love:10张帅子
何壮壮love:45张帅子
小怪love:100张帅子
胡图图到张帅子的最短路径
确定不是恋爱路径?
算法实现
先看猛料再看是否实现思路
// 定义深度优先搜索状态
struct DepthFirstSearchFLag {
int index; // 当前索引
bool visited[MaxSize]; // 顶点访问状态
};
// 定义最短路径状态
struct ShortPathFLag {
DepthFirstSearchFLag Flag; // 深度优先搜索状态
int end; // 结束顶点索引
int stepNum; // 步数
int m_Weight; // 当前路径权重
int ArgsWeight; // 参数路径权重
int SevePath[MaxSize]; // 保存路径
int ShortPathValue[MaxSize];// 最短路径值
};
// 寻找图中任意两顶点间的最短路径。
void ShortPath(const Graph& graph, ShortPathFLag& ShortPathFLag) {
// 获取当前顶点索引和终点索引
int& index = ShortPathFLag.Flag.index;
int& end = ShortPathFLag.end;
// 获取搜索状态
auto& visited = ShortPathFLag.Flag.visited; // 记录已访问顶点
auto& SevePath = ShortPathFLag.SevePath; // 记录路径
auto& ShortPaths = ShortPathFLag.ShortPathValue; // 记录最短路径值
int& stepNum = ShortPathFLag.stepNum; // 记录当前步数
int& ArgsWeight = ShortPathFLag.ArgsWeight; // 记录当前路径长度
int& Weight = ShortPathFLag.m_Weight; // 记录最短路径长度
// 如果到达终点,更新最短路径并输出
if (index == end) {
// 输出当前路径
for (size_t i = 0; i < stepNum; i++) {
cout << graph.List[SevePath[i]]->value << " ->";
}
// 输出当前路径长度
cout << "\t该路径对应的恋爱值 (Love)是:" << ArgsWeight << endl;
// 如果当前路径更短,更新最短路径
if (Weight > ArgsWeight) {
Weight = ArgsWeight;
// 更新最短路径值
int conut = stepNum * sizeof(conut);
memcpy(ShortPaths, SevePath, conut);
}
}
// 获取当前顶点的相邻未访问顶点
int currentIndex = index;
Edge* current = graph.List[index]->First;
while (current) {
currentIndex = current->AdjVertex;
if (!visited[currentIndex]) {
// 标记顶点为已访问,更新路径和权重,继续搜索
visited[currentIndex] = true;
SevePath[stepNum++] = currentIndex;
ArgsWeight = ArgsWeight + current->Weight;
index = currentIndex;
ShortPath(graph, ShortPathFLag);
// 搜索返回后重置状态,继续搜索其他相邻顶点
visited[currentIndex] = false;
SevePath[--stepNum] = 0;
}
current = current->next;
}
}
// 寻找图中任意两顶点VertexValueFirst和VertexValueSecond间的最短路径。
void ShortPath(const Graph& graph, VertexValue VertexValueFirst, VertexValue VertexValueSecond){
// 初始化搜索状态
ShortPathFLag Flag{}; // 搜索状态
Flag.m_Weight = INT_MAX; // 初始化最短路径长度为最大值
const int VertexSize = graph.VertexSize; // 顶点数
// 获取起点和终点索引
Flag.Flag.index = Location(graph, VertexValueFirst); // 起点索引
Flag.end = Location(graph, VertexValueSecond); // 终点索引
// 如果起点和终点存在,执行搜索
if (Flag.Flag.index != VertexSize && Flag.end!= VertexSize) {
// 输出搜索信息
cout << VertexValueFirst << "到" << VertexValueSecond << "最短路径:" << endl;
// 执行深度优先搜索
ShortPath(graph, Flag);
// 输出搜索结果
cout << endl;
cout << "最小路径长度为:" << Flag.m_Weight << endl; // 输出最短路径长度
cout << "路径:";
// 输出最短路径
auto& Path = Flag.ShortPathValue; // 最短路径值
int i = 0;
while (i < MaxSize && Path[i]>0) {
cout << graph.List[Path[i]]->value << " ";
i++;
}
cout << endl;
}
}
算法思想
- 获取状态信息,包括当前索引、终点索引、步数等。
int& index = ShortPathFLag.Flag.index;
int& end = ShortPathFLag.end;
auto& visited = ShortPathFLag.Flag.visited;
auto& SevePath = ShortPathFLag.SevePath;
auto& ShortPaths = ShortPathFLag.ShortPathValue;
int& stepNum = ShortPathFLag.stepNum;
int& ArgsWeight = ShortPathFLag.ArgsWeight;
int& Weight = ShortPathFLag.m_Weight;- 如果到达终点,更新最短路径并输出。
if (index==end){
//输出路径
//更新最短路径
}- 获取当前顶点的相邻未访问顶点。
int currentIndex = index;
Edge* current = graph.List[index]->First;
while (current) {
currentIndex = current->AdjVertex;
if (!visited[currentIndex]){
//找到相邻未访问顶点
}
current = current->next;
}- 标记顶点为已访问,更新路径和权重,继续搜索。
visited[currentIndex] = true;
SevePath[stepNum++] = currentIndex;
ArgsWeight = ArgsWeight + current->Weight;
index = currentIndex;
ShortPath(graph, ShortPathFLag);
- 搜索返回后重置状态,继续遍历其他相邻顶点。
visited[currentIndex] = false;
SevePath[–stepNum] = 0;