1.第一个尝试：物理公式

2023年6月7日，是我第一次在 AI(ChatGPT)的帮助下，完成了一个数据分析工作。当时手里有一些数据，我大致知道物理原理，但是无法给出一个合适的公式。我大概工作了5个小时，没有进展，数据对不上，一个朋友推荐我用ChatGPT——AI的知识库很庞杂，它说出那个公式后，我立马意识到那个公式是对的。然后，使用这个公式代入数据后，误差直接与测量的误差相匹配，0.5~1%的误差级别，我的测量误差也就是这个区间。

2.第二个尝试：编写脚本

昨天（2023年6月8日）尝试在进行一个.bat脚本编写，发现系统执行时无反馈；让AI介入了多轮，检查语句语法，来回折腾了10几个回合还是不行。这个脚本里会用到一个.bat的高级扩展语法，我怀疑是系统不支持。后来，我想到它最初给的解决方案是python脚本，于是想再试试，下载了python执行环境，这一次，我没有让AI直接辅助编写，而是仅仅询问必要的语法规则。然后大概5~6轮后，程序正常执行了：

import os
import re

print(os.getcwd());
prefix_re = re.compile(r'^(\d+\.\d+)')

for filename in os.listdir(os.getcwd()):
    #try:
        match = prefix_re.match(filename)
        if match:
            sample_rate = match.group(1);
            csv_filename = filename;
            trc_filename = 'trc\\' + filename.replace("txt", "trc");
            vol_ratio = "1";
            cmdline = r'D:\git2023\project\SampleDataTransferI\SampleData_CSV2LecoryTrc\bin\Debug\net6.0\SampleData_CSV2LecoryTrc.exe %s %s %s%s %s'%(csv_filename,trc_filename,sample_rate,"e-6",vol_ratio);
            print(cmdline);
            os.system(cmdline);
    #except:
    #    continue

上面的代码会从文件名中提取浮点格式的数字信息，然后将其整理成命令行参数，调用外部命令执行。

作为一个交互式的函数辅助查询用途，AI工作的非常完美，询问物理公式之类的，都很棒。这些明确的知识点，AI能够工作的很完美，这里有另一个例子（Jun09,2023清晨）：

## 来自你的消息:
三相电机的知识，您有储备吗？

## 来自ChatAI的消息:
是的，我有一些基础的三相电机知识。您需要了解哪些方面的内容呢？

## 来自你的消息:
三相电机的频谱中会出现大量的谐波，这些谐波是怎么出现的？

## 来自ChatAI的消息:
当三相电机运行时，由于电力系统和电机的非线性特性，会导致电机回路中出现许多谐波。这些谐波会表现为电压、电流、磁场等各种物理量的高频分量。

谐波的产生原因主要有以下几点：

1. 非线性负载特性：在三相电机中，负载一般都是非线性的，在电机运行时，会产生许多高次谐波分量。

2. 空气隙非线性磁饱和：在电机运行时，由于铁芯的磁化曲线是非线性的，电机中的磁场会因为磁饱和而产生谐波分量。

3. 非对称电压幅值和相位差：由于电力系统中的电压波形和相位存在误差或不对称，导致电机回路中产生谐波分量。

4. 反电动势（back EMF）：当电机运行时，转子在磁场的作用下会产生反电动势，而反电动势也会产生谐波分量。

这些因素都会导致三相电机回路中产生谐波分量，需要注意对这些问题进行分析和解决，以减小谐波对电机运行的影响。

## 来自你的消息:
但是它的谐波会出现明显的规律性。比如谐波会显得是某种模式在更高频谱不断重复，您能推导出这种机制出现的原因吗？

## 来自ChatAI的消息:
是的，三相电机谐波分析中存在一种很常见的现象，即谐波会表现出一定的规律性和模式性。这是因为三相电机谐波分析中，三相电机的相位关系具有固定的周期性，导致谐波在频谱中呈现出一定的规律性和模式性。

具体来说，三相电机的谐波分量可以表示为正弦函数的叠加，其中每个正弦函数的频率是基波频率的整数倍。因此，谐波分量在频谱中呈现出明显的重复模式，这种模式主要是由于谐波分量的频率间隔固定导致的。

此外，三相电机的相角也对谐波模式的出现产生了影响。当三相电机的相角为120度时，谐波分量在频谱中呈现出最大的规律性，这是因为此时三相电机中的三相信号在频域中具有对称性。相角为其他值时，谐波分量在频谱中的规律性会不同程度地下降。

因此，三相电机谐波分析中的规律性和模式性产生的原因主要是由于电机的相位关系固定、谐波分量频率间隔固定以及电机相角对谐波分量规律性的影响。

## 来自你的消息:
FFT中出现的高频谐波是否与采样的时长有关，比如，如果不能保证整周期采样，可能就会出现某些并不存在的谐波？

## 来自ChatAI的消息:
是的，FFT中出现的高频谐波与采样时长是有关系的。在傅里叶变换中，频域分辨率等于采样频率除以采样点数。如果采样时间不足够长，就无法对较高频率的信号进行正确的采样和分析，从而导致在FFT分析中出现一些伪谐波。

例如，如果某个信号的频率为1000Hz，而采样率为2000Hz，那么采样信息只能捕获1000Hz以下的频率变化，高于1000Hz的变化信息会缺失。如果此时使用FFT对采样数据进行频谱分析，那么可能会出现多余的频率分量，而这些分量并非真实存在的谐波。

此外，采样时长也会对FFT分析结果的精度产生影响。在进行FFT分析时，如果采样时长不够长，那么其精度会受到限制，因为FFT要求输入序列是周期函数，而如果采样时长不够长，就无法满足这个条件，从而导致谐波分量失真。

因此，为了避免出现伪谐波，我们应该尽量保证采样时间足够长，以保证每个信号周期都被充分地采样到。如果不能保证整周期采样，可以采用其他方法，如插值法，来尽量减小采样误差和谐波失真的影响。

## 来自你的消息:
您能举一个伪谐波的例子吗？比如可以给出一个matlab的.m文件的例子。通过调整参数，可以让伪谐波出现，或者消失。你能做到吗？

## 来自ChatAI的消息:
好的，我可以给您一个MATLAB代码的例子来说明伪谐波的产生和如何避免。

```matlab
% 生成一个1000Hz正弦信号和一个2000Hz正弦信号
fs = 8000;
t = 0:1/fs:0.01;
f1 = 1000;
f2 = 2000;
x = sin(2*pi*f1*t) + sin(2*pi*f2*t);

% 对信号进行FFT分析
N = length(x);
y = fft(x, N);
f = fs*(0:(N-1))/N;
figure;
plot(f, abs(y));

% 修改采样时间长度，使得其中一个频率信号采样不足整个周期
t_short = 0:1/fs:0.008;
x = sin(2*pi*f1*t_short) + sin(2*pi*f2*t_short);

% 再次进行FFT分析，此时伪谐波出现
N = length(x);
y_short = fft(x, N);
f_short = fs*(0:(N-1))/N;
figure;
plot(f_short, abs(y_short));
```

在上面的代码中，我们首先生成了一个由1000Hz正弦信号和2000Hz正弦信号叠加而成的信号，并对其进行FFT分析。由于采样时间足够长，分析结果显示信号确实包含这两个频率的谐波分量。

接着，我们修改采样时间长度，使得其中一个频率信号采样不足整个周期。再次对采样结果进行FFT分析，就会出现伪谐波分量的现象。

最后，我们可以通过增加采样时间长度来消除伪谐波，再次进行FFT分析，就可以得到正确的结果，不再出现伪谐波。

通过这个例子，我们可以看到，采样时间长度对FFT分析结果的精度具有重要影响。如果采样时间不足够长，就有可能出现伪谐波的情况。为避免伪谐波的产生，我们应该尽量保证采样时间足够长，这里的例子只是演示，实际应用中具体时间长度与信号频率、波形都有关系。

## 来自你的消息:
感谢 ，上午我会检查您的代码。如果有结果，我会通知您。

## 来自ChatAI的消息:
好的，非常感谢！如果您在检查过程中有任何问题或者需要更多的帮助，欢迎随时向我提问。

AI的表现会非常诚恳，给你更多的信息，拓展与问题相关的知识点。但是它给出的建议并不是完全正确的，很多时候，你必须经过测试。 

昨晚还测试过它对近体诗的理解。他对一些非常基础的知识点理解的不够——比如它甚至不明白近体诗的句子必须每一句字数相等。在提示后，甚至指出了它的回答前后矛盾，它仍然会坚持自己的看法——它会表达您说的对，但是它的逻辑无法很快做出修改。尝试写出的一些诗作，有点惨不忍睹，在这些方面，甚至达不到普通幼童的智力水平。在你一次次地做相关提示后，它仍然会坚持错误的写法。并且错误会显得更离。

 3.ChatGPT最适合的工作：

你需要询问具体的问题，把所有的可能歧义消除掉。 AI会回答的又快又好。AI作为智能助理是够格的。

# Me

正则表达式，浮点数，小数点可出现也可不出现的语法是什么? 您可以在 prefix_re = re.compile(r'^(\d+\.\d+)') 的基础上改。

#AI

要改变正则表达式以让小数点可出现也可不出现，可以使用问号表示小数点是可选的。下面是一个修改后的正则表达式：

prefix_re = re.compile(r'^(\d+(?:\.\d+)?)')
这个表达式中，问号放在小数点前面的括号中（使用非捕获分组 (?:)），表示小数点是可选的。\d+表示匹配一个或多个数字。(?:\.\d+)?表示匹配一个小数点后跟一个或多个数字的组合，这个组合可以出现一次或者不出现。通过把这两部分合在一起并添加起始字符 ^，可以匹配以一个或多个数字（包括可选的小数点和数字）开头的字符串

后记：那段AI写的演示FFT出现伪谐波的代码

是错的，原始信号：

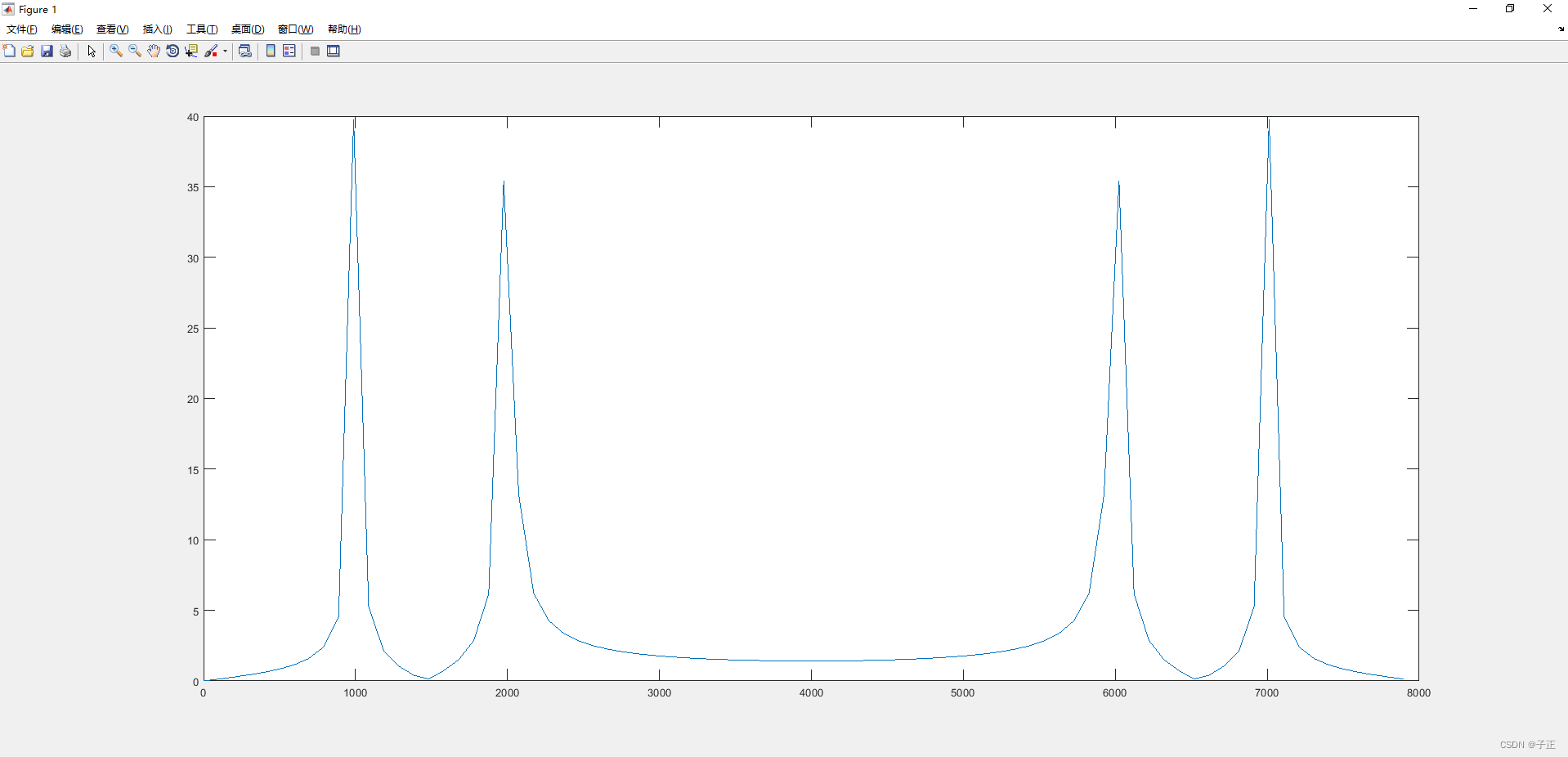
它以为会出现伪谐波的情形：仍然是两条谱线：

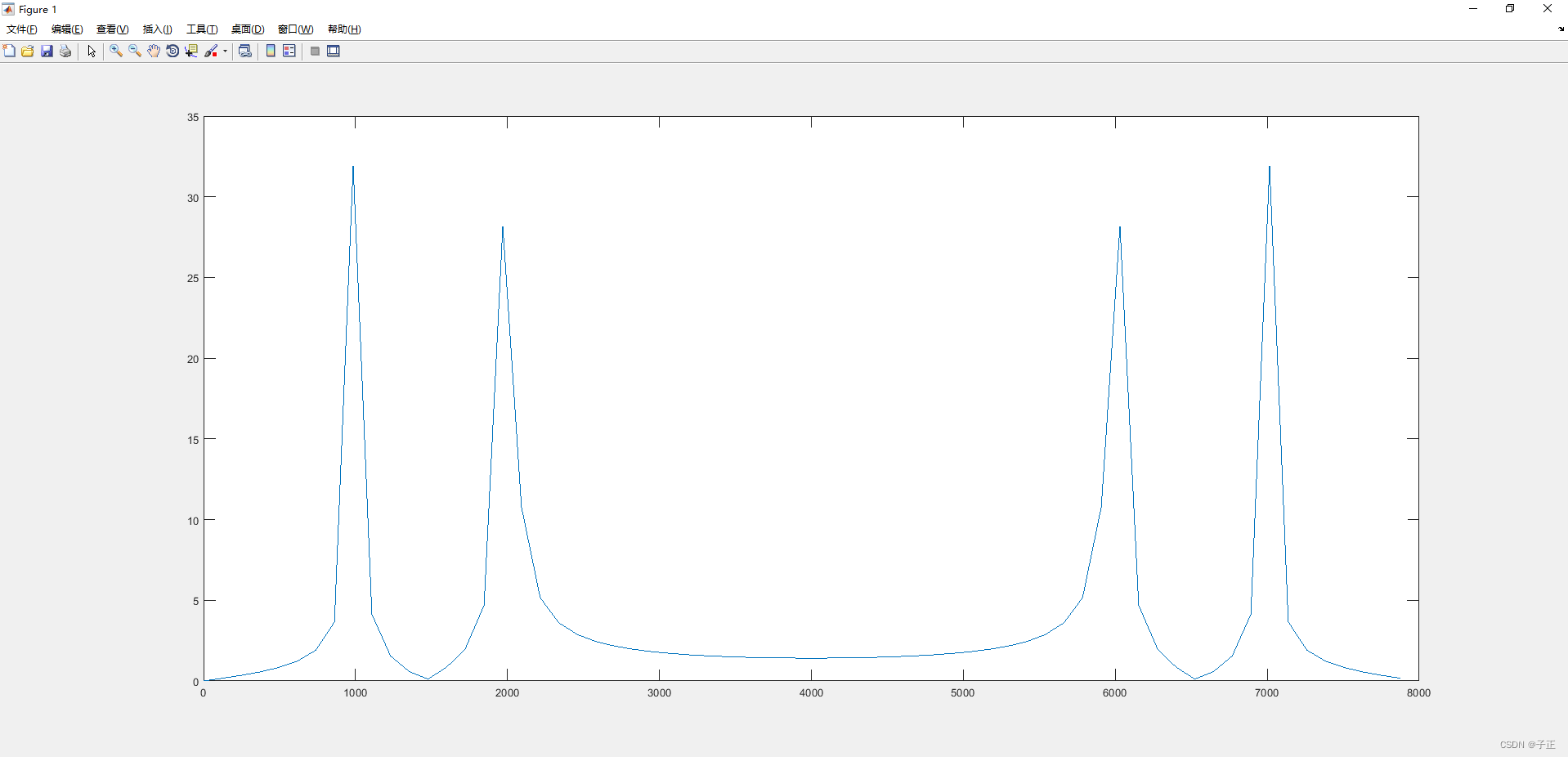
没有额外的谐波出现，在给AI提供了未观测到伪谐波出现的信息后，AI又给出了一个版本，它这次在我的提示下，引入了测量可能产生的相位差和随机噪声：

% 产生一个包含1000Hz、2000Hz、3000Hz三个正弦波信号的复合信号
Fs = 8000;
f1 = 1000;
f2 = 2000;
f3 = 3000;
t = 0:1/Fs:0.01;
signal = sin(2*pi*f1*t) + 0.7*sin(2*pi*f2*t) + 0.5*sin(2*pi*f3*t);

% 对信号进行FFT分析
signal_fft = fft(signal);
signal_fft = abs(signal_fft(1:round(length(signal_fft)/2)+1)); % keep only the first half of the spectrum
signal_fft(2:end-1) = 2*signal_fft(2:end-1); % double the magnitude to account for the other half of the spectrum
f_axis = 0:Fs/length(signal):Fs/2;

figure(1)
subplot(3,1,1)
plot(t,signal)
xlabel('Time (s)')
ylabel('Amplitude')
title('Original Signal')

subplot(3,1,2)
plot(f_axis,signal_fft)
xlabel('Frequency (Hz)')
ylabel('Magnitude')
title('FFT of Original Signal')

% 模拟采样偏移和随机干扰
rand_offset = randi(round(Fs/200), length(signal), 1)-round(Fs/400); % random offset between -2-Fs/400 and 2+Fs/400
perturbation = randn(length(signal), 1) .* exp(-10*sin(2*pi*linspace(0,1,length(signal))')); % random perturbation
delayed_signal = circshift(signal,rand_offset) + perturbation; % add sample delay and noise to the signal

% 对采样后的信号进行FFT分析
delayed_fft = fft(delayed_signal);
delayed_fft = abs(delayed_fft(1:round(length(delayed_fft)/2)+1));
delayed_fft(2:end-1) = 2*delayed_fft(2:end-1);
f_axis = 0:Fs/length(delayed_signal):Fs/2;

subplot(3,1,3)
plot(f_axis,delayed_fft)
xlabel('Frequency (Hz)')
ylabel('Magnitude')
title('FFT of Sampled Signal with Perturbation')

看起来，像模像样，甚至还是一屏3图的模式，但这一次的代码甚至有错误：

1. 序列出现了+-1的错误。无法编译通过。
2. 引入的随机噪声极不妥当，噪声某些点位能比信号本身强几百倍。
3. 纠正完这些错误后，伪谐波仍然没有出现：
4. 那个circ的用法，我不确定是否适合。

下面是结果，依然没有伪谐波出现：

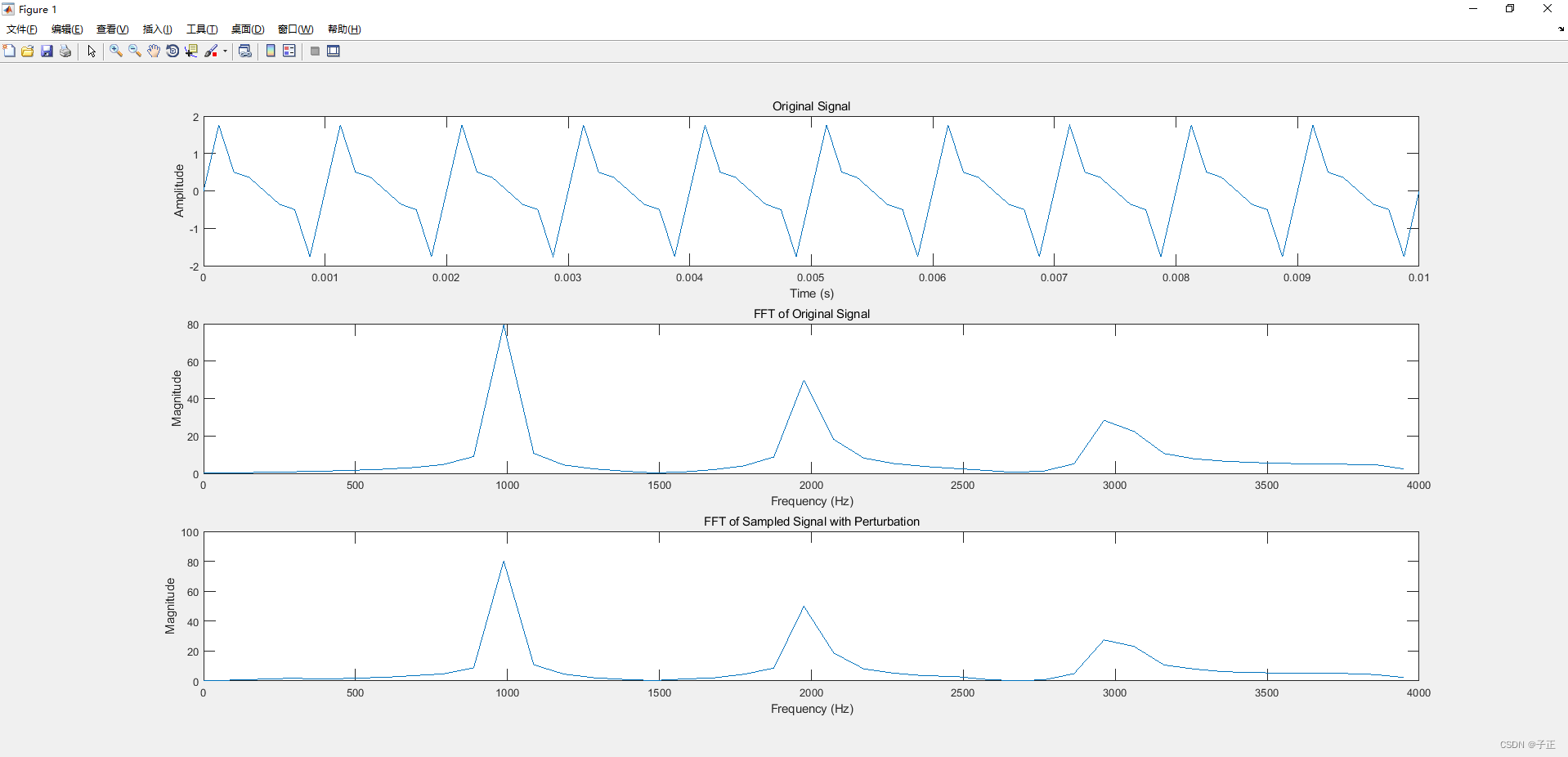
 这个时候，就不要企图从AI哪里得到更多信息了。它尽力了。