你好,我是郭震(zhenguo)
今天介绍强化学习第九篇:Q-learning算法
前面我们介绍强化学习基本概念,马尔科夫决策过程,策略迭代和值迭代,这些组成强化学习的基础。
从今天开始逐步介绍常用强化学习算法,从最简单的Q-learning算法开始。简单并不代表不常用,有的简单会是经典,Q-learning算法就是这样的例子。
1 迷宫游戏
假设我们有一个迷宫地图,其中包含多个状态(格子),每个格子可以采取上、下、左、右四个动作进行移动。目标是从起始位置找到迷宫的出口,即到达终点位置。
首先,我们需要定义迷宫地图的状态和动作。状态可以表示为迷宫中的每个格子,动作可以表示为上、下、左、右四个方向。
如下图所示,对于图示白色格子,假定智能体走到这里,它只能向上、下运动,因为左右两侧是障碍物:
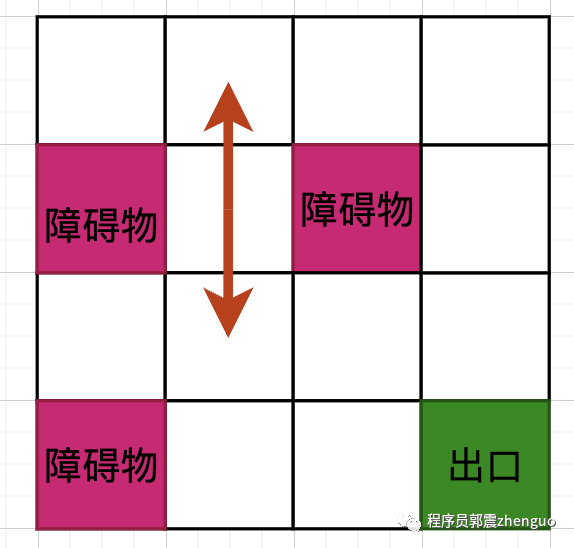
由此引出Q表,Q表用于存储每个状态动作对的Q值估计。
在图示迷宫中,Q表是一个二维表格,用于存储每个状态动作对的Q值估计。迷宫地图有4行4列,共有16个格子,且每个格子可以采取上、下、左、右四个动作,那么Q表的大小:[16,4] 二维表格。每一行对应着一个状态,每一列对应着一个动作。
Q表样子:
上 下 左 右
0 Q(0,0) Q(0,1) Q(0,2) Q(0,3)
1 Q(1,0) Q(1,1) Q(1,2) Q(1,3)
2 Q(2,0) Q(2,1) Q(2,2) Q(2,3)
3 Q(3,0) Q(3,1) Q(3,2) Q(3,3)
4 Q(4,0) Q(4,1) Q(4,2) Q(4,3)
5 Q(5,0) Q(5,1) Q(5,2) Q(5,3)
6 Q(6,0) Q(6,1) Q(6,2) Q(6,3)
7 Q(7,0) Q(7,1) Q(7,2) Q(7,3)
8 Q(8,0) Q(8,1) Q(8,2) Q(8,3)
9 Q(9,0) Q(9,1) Q(9,2) Q(9,3)
10 Q(10,0) Q(10,1) Q(10,2) Q(10,3)
11 Q(11,0) Q(11,1) Q(11,2) Q(11,3)
12 Q(12,0) Q(12,1) Q(12,2) Q(12,3)
13 Q(13,0) Q(13,1) Q(13,2) Q(13,3)
14 Q(14,0) Q(14,1) Q(14,2) Q(14,3)
15 Q(15,0) Q(15,1) Q(15,2) Q(15,3)下面图是给每个状态编号后的示意图,更好帮助你理解Q表:

Q表里的每个值代表什么意义?
Q值表示在该状态下采取该动作所获得的长期回报估计。比如Q(11,2)表示在状态11下,采取动作编号2后的长期回报值。
2 归纳
借助上面迷宫游戏,我们归纳出Q-learning算法相关的抽象解释。
Q值定义:
Q值是一个表格,用于存储每个状态动作对的估计价值。对于给定的状态
s和动作a,Q值表示在状态s执行动作a所获得的长期回报估计。
Q-learning算法核心之更新规则:
Q-learning使用迭代的方式更新Q值,通过不断更新Q值来逐步逼近最优策略。更新规则如下:
其中,表示在状态s执行动作a的值, 是学习率(0 < α <= 1), 是执行动作a后获得的即时奖励, 是折扣因子(0 <= <= 1), 是执行动作a后转移到的下一个状态,是在下一个状态下选择的动作,表示在下一个状态下所有可能动作中选择值最大的动作。
更新规则的含义是,通过将当前Q值与新估计的Q值加权平均,使Q值逐步收敛到最优值。其中, 控制了新估计值的权重, 控制了对未来回报的重视程度。
通过不断地执行更新规则,Q-learning算法能够逐步学习到最优的Q值,并根据Q值选择最佳的动作来达到最优策略。
3 Q-learning算法
下面是完整的Q-learning算法:
Step1:初始化Q表:对于每个状态-动作对(s, a),将Q(s, a)初始化为一个随机值或者初始值。
Step2:迭代更新Q值:
Step2.1 选择一个初始状态s。
Step2.2 在当前状态s下,根据一定策略选择一个动作a。例如可以使用ε-greedy策略,在一定概率ε内选择随机动作,否则选择具有最大Q值的动作。
Step2.3 执行动作a,观察获得的奖励r以及转移到的下一个状态s'。
Step2.4 根据Q值的更新规则,更新Q(s, a):
将状态更新为下一个状态
s',并重复以上步骤直到到达终止状态。
Step3 重复步骤Step2,直到达到指定的迭代次数或者满足停止条件。
Step4 返回学习到的Q表作为最优策略。
这个算法的核心是通过不断与环境的交互,根据即时奖励和未来奖励更新Q值,从而逐步学习到最优策略。在训练过程中,智能体通过不断尝试并观察结果,不断调整Q值,直到找到最优的动作选择策略。
感谢你的点赞和转发,让我更新更有动力









![[蓝桥杯 2018 国 B] 矩阵求和](https://img-blog.csdnimg.cn/6327b597c2284e62a1d133003d7e6a71.png)