今儿在帮别人跑一段python代码,实际上我对python并不熟悉,只能边摸索边尝试。选择了pycharm这个工具。
一.怎么安装python使用的库文件
能用来安装python的库文件的,有很多种办法,这里只介绍pip和pip3。因为pip和pip3的优势是能自行解决依赖问题。
1. 搞清楚pip和pip3的区别
网上能搜到的pip和pip3的区别,都是很官方的回答,通常是pip用于python1.x和python2.x,而pip3用于python3.x,这个说法没问题,但是使用起来还有会有一些疑惑。换句话说,我理解,就是pip下载下来的库是给python1和python2用的,pip3下载的库是给python3用的。所以如果你使用的是python3.x的版本,记住要用pip3下载库文件。
2. 在linux中安装pip3和pip
在linux的命令行中安装pip3,可以用这个命令:
sudo apt install python3-pip
同样的,安装pip,可以用这个命令:
sudo apt install python-pip
3. 怎么使用pip和pip3
有在命令行中使用和在pycharm中使用,两种方法。实际上都是一样的,只是在pycharm中将命令行通过可视化界面来实现了。归根结底是这样一个命令。
3.1. 在命令行利用pip和pip3安装库文件
在此只讲解linux下的,windows下的类似。
python -m pip install libsora //写法1
pip install libsora //写法2
这是利用pip下载的库。两种用法是一致的。
python3 -m pip install libsora //写法1
pip3 install libsora //写法2
这是利用pip3下载的库。两种用法是一致的。
3.2. 在pycharm中利用pip和pip3安装库文件
在pycharm使用pip和pip3安装库文件的方法相比较来说简单一些。
打开pycharm的界面,如下图。
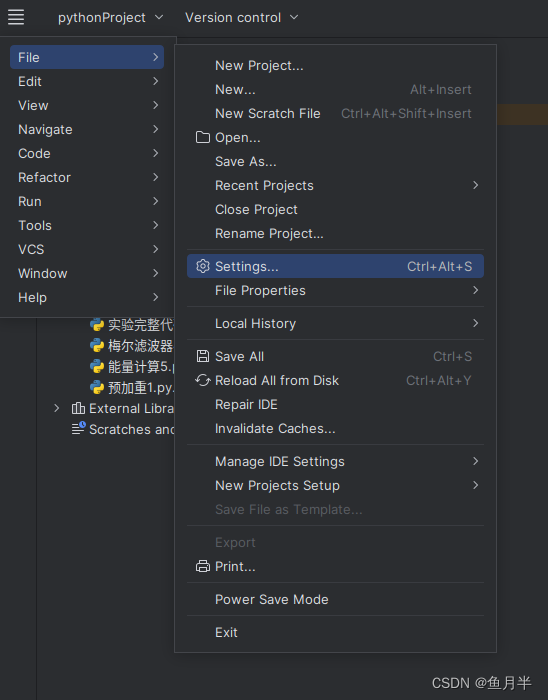
不同的版本和操作系统,界面可能有差别,但路径是不会变的,就是
file->Settings…
这么一个路径,打开以后在搜索栏中输入pip,能搜出下面内容,选择Python Interpreter,出现右侧内容,即加载在这个工程中的库文件。
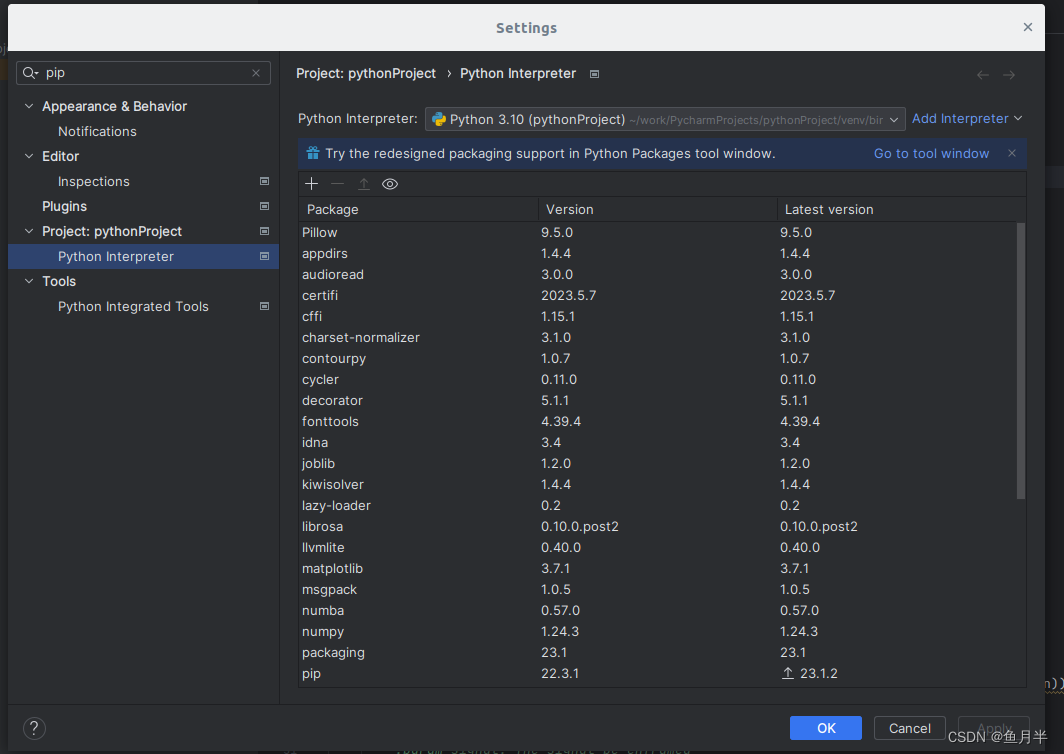
注意!
首先需要介绍pycharm新建一个工程文件时,他默认给每个工程文件一个干净的库文件的环境变量,当然你也可以选择将系统全局的环境变量添加给这个工程,或者在不同的python版本及对应的环境变量中进行切换。
在Python Interpreter后侧的下拉框中进行环境变量的选择,下拉框默认只有一个新建的本工程的环境变量,如果想要增加别的环境变量,可以点击“Add Interpreter”进行更多的环境变量的添加。下拉框下面的显示框中所显示的库文件,即选中的环境变量中所包含的库文件。
点击“Add Interpreter”按钮后选择“Add Local Interpreter”,弹框如下。
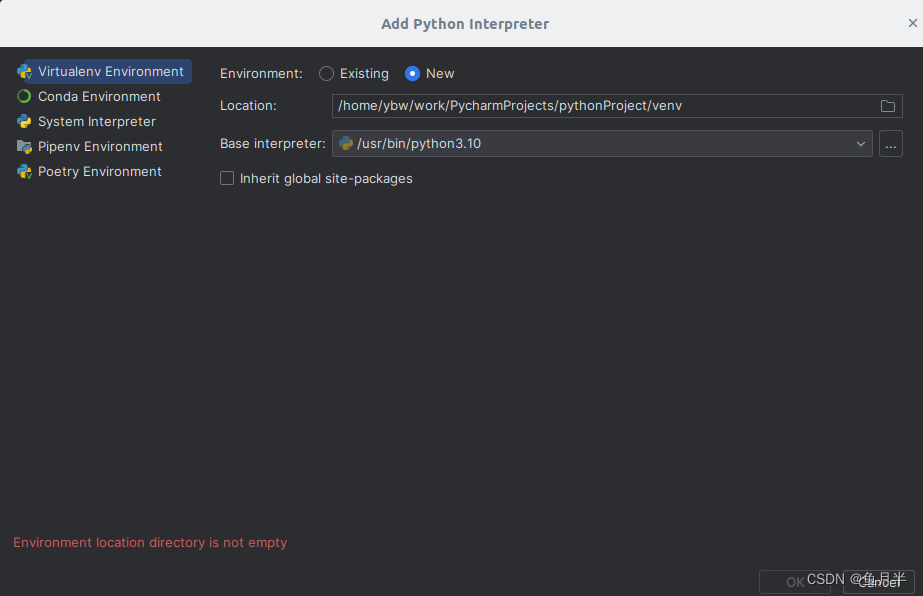
图中所示的第一个tab页,“Virtualenv Environment”,即创建本工程时新建的环境变量,包含了环境变量库文件保存的地址,以及运行的python版本。
图中所示的第二个tab页,是另一个库文件下载工具,这里不介绍。
图中所示的第三个tab页,“System Interpreter”,即操作系统自带的环境变量,以不同的python版本作区分,可从多个版本中进行选择。如图。
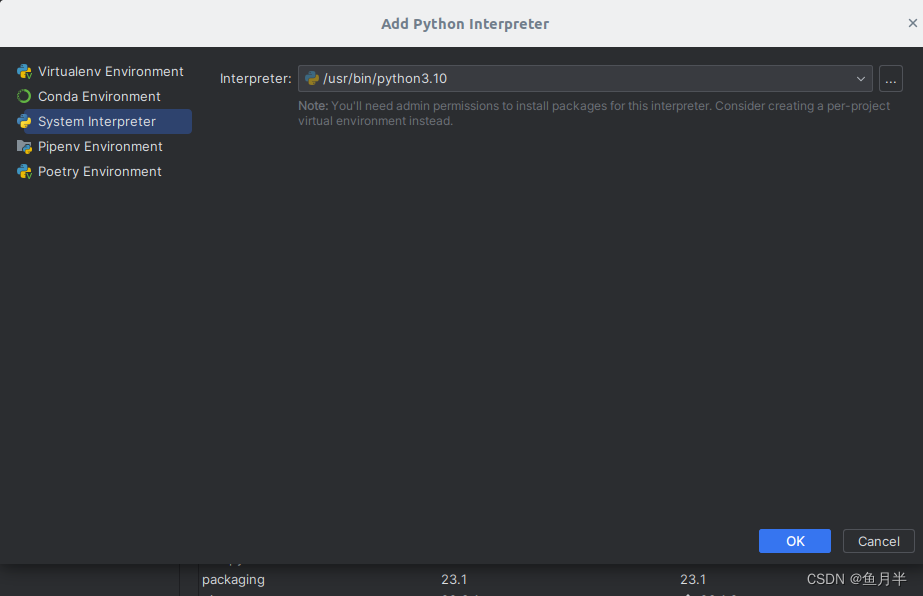
选中相应的python版本,即选中了相应的库文件。
点击“ok”按钮,即将相应的内容加入了前一窗口的下拉菜单中,供选择。
在库文件显示的框中,可以看见有一个"+"或者“-”号,点击“+”号则可进行库文件的增加,点击“-”号进行库文件的移除。这里所做的库文件的增减操作,只会体现在所选中的环境变量中。
点击“+”号,弹窗如下。
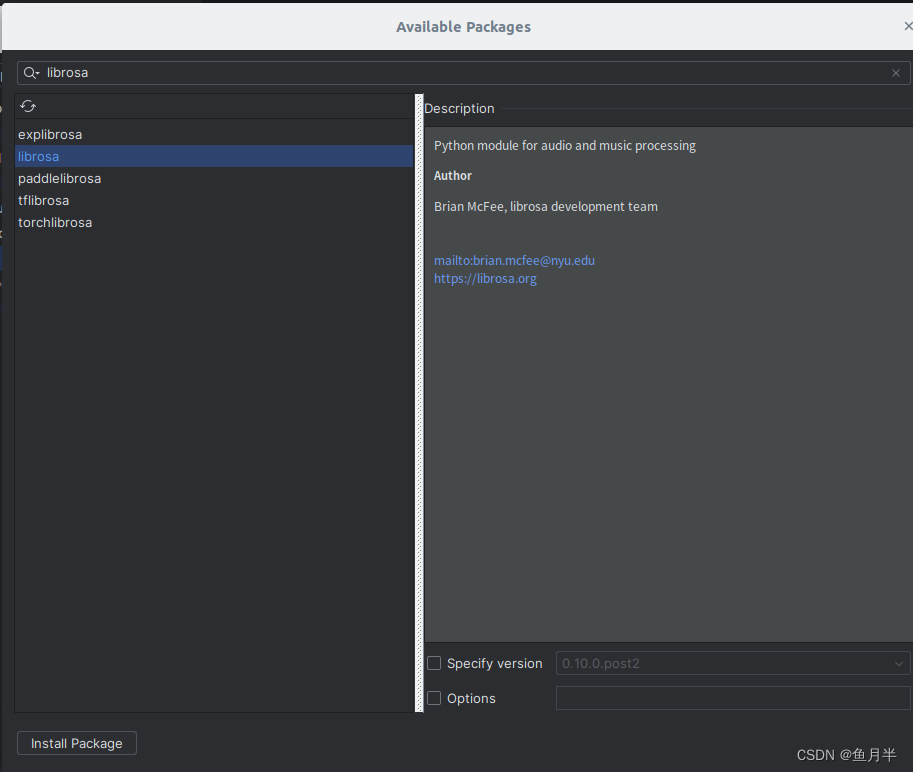
这就是“Available Packages”窗口,在此进行所选环境变量中的库文件的增减。
在搜索框中输入,如“librosa”,则可搜到相应库文件,并显示在左侧栏中,选中后,点击下面按钮“Install Package”,顺利的话,则安装成功。
在右侧“Specify version”可以选择库的版本。针对特别需求所设。
“Options”中,就类似于在命令行中添加一些参数,可以添加例如仓库源的相关内容。比如要使用清华的pip仓库源,可以在此添加“–trusted-host mirrors.aliyun.com”。
二.在安装库文件的过程中踩到的坑
1.不同的CPU即不同的指令集,可能有些库未做适配
一开始,在一台龙芯3A5000的loongnix系统上做开发,库文件一直安装失败,后来换了amd的ubuntu,就很顺利了。所以库文件安装失败,可能是CPU或者操作系统的适配问题。
2.pycharm中使用的命令pip不一定是python1的pip
在pycharm中经常可见的是pip命令,但是命名选择的是python3.x,所以一开始有些疑惑,这个pip对不对,所以一直在想办法把pip改成pip3。后来才反应过来,这里的pip,指的是下面
python3 -m pip install libsora //写法1
pip3 install libsora //写法2
第一句中的-m后面的那个pip。