0. 内容

1. 基于BA的VIO融合
优化的方法学会之后,滤波的方法也就会了。

具体的求解BA问题参考的是SBA的论文,使用的是LM算法(里面有个关于权重μ的计算方法,不同人的实现可能不一样,这些都是实现细节)

camera两个观测之间的相对位置(pq的变化)可以通过两次观测知道,但是IMU在两个时刻的观测量需要进行积分才能知道,而且IMU数据频率一般比Camera频率高,所以需要逐步地积分才能得到运动情况。
2. 最小二乘问题的求解
牛顿法,将loss function直接Taylor二阶展开,高斯牛顿法是将原函数f(x)一阶展开,再进行求解。

解法分为直接解和迭代解:

马鞍面复习:
2.1 一阶法
下降法(如果方向选择为梯度反方向则就为DL中的梯度下降法,此处叫最速下降法):


最速下降法:不易收敛;牛顿法:H计算量大。
阻尼法,在牛顿法基础上增加一个
Δ
x
\Delta x
Δx的正则项,使其不会太大(此处仍是一阶法,不是LM法):

阻尼法的阻尼是加在H上的
μ
\mu
μ
为方便起见,可将残差stack起来成向量(也可以携程sum of的形式,但向量可供讨论具体小f的一些性质,相应地,雅克比J和海塞H也要相应地写为向量形式)

F(x)是cost function,最简单的例子:
m
i
n
F
(
x
)
=
1
2
∣
∣
f
(
x
)
∣
∣
2
2
minF(x)=\frac{1}{2}||f(x)||_2^2
minF(x)=21∣∣f(x)∣∣22
2.2 二阶法
2.2.1 Gauss-Newton

损失函数F(x)对
Δ
x
\Delta x
Δx的一阶导数可记作b,也可直接写F(x)
′
^\prime
′
2.2.2 LM
2.2.2.1 LM阻尼因子 μ \mu μ初值的选取方法

τ
\tau
τ的设定是根据经验值而来,当前x距离
x
∗
x^*
x∗较近时,取二阶近似,初值
μ
0
\mu_0
μ0就设的小一些,乘较小的
τ
\tau
τ,距离
x
∗
x^*
x∗较远时,初值就设的应该较大,保证下降的较快,取一阶近似,乘接近于1的
τ
\tau
τ
这里高翔补充了一点,:广义的韦达定理保证所有的特征值 λ i \lambda_i λi之和跟矩阵的trace是一样的。
所以这里取 m a x J T J i i max{J^TJ_{ii}} maxJTJii矩阵的对角线的最大元素是有道理的,即可以有这样的先验: J T J i i J^TJ_{ii} JTJii的对角线最大元素跟 J T J i i J^TJ_{ii} JTJii特征值的最大值是在同一个数量级,所以可取对角线最大元素来近似最大特征值。
2.2.2.2 LM阻尼因子 μ \mu μ的更新策略
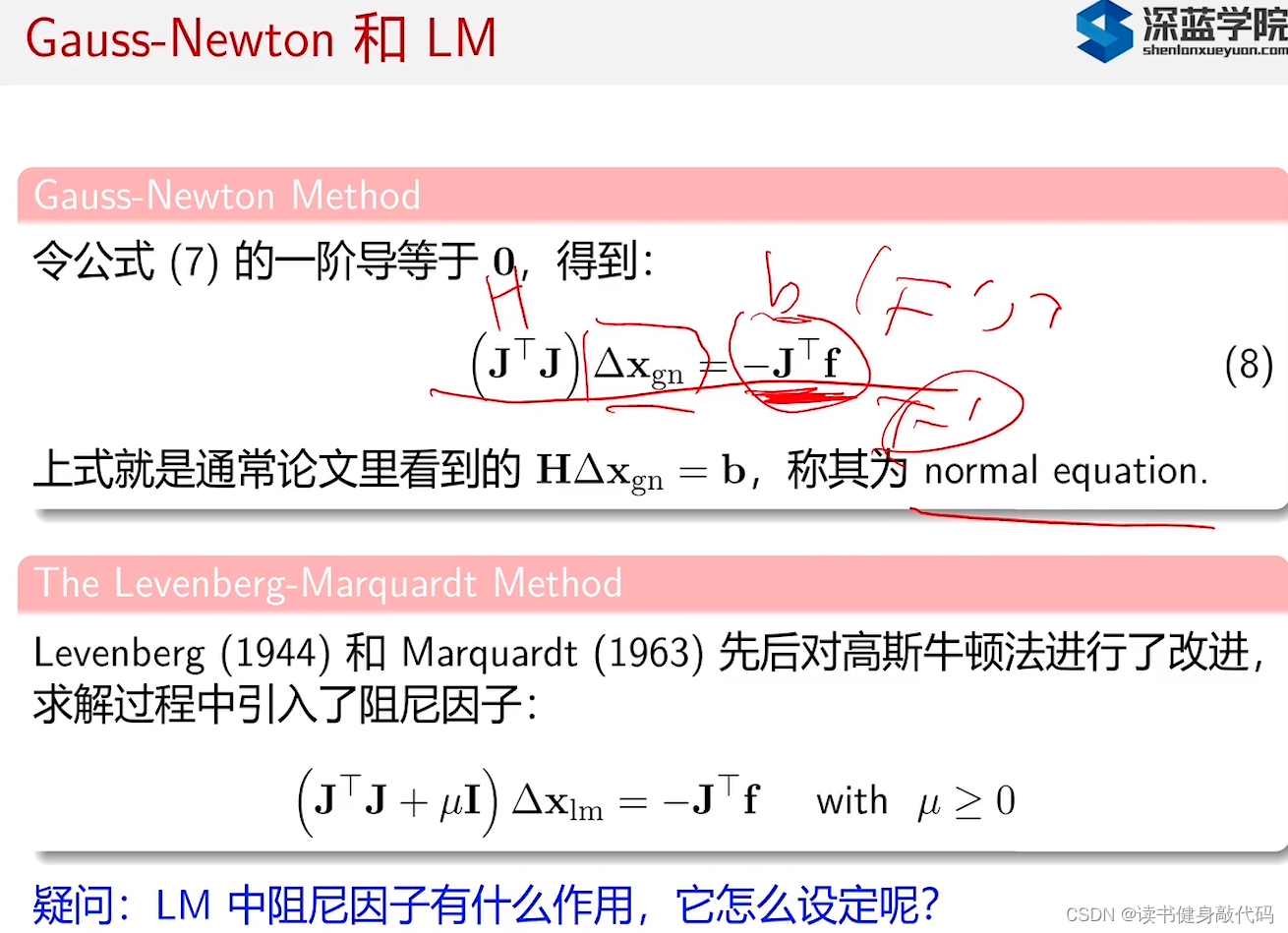
定性分析,看上面的
Δ
x
\Delta x
Δx的解析形式,
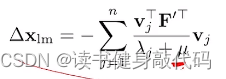
μ
\mu
μ处于分母上,增大阻尼
μ
\mu
μ会减小步长,也符合“阻尼”的直观感受:当某次
Δ
x
\Delta x
Δx使得cost function增大,则应该增大阻尼使
Δ
x
\Delta x
Δx变小,减小步长;反之,如果cost function在下降则应该减小阻尼
μ
\mu
μ,增大步长,加快收敛速度。

上述推导说明分母一定是>0的,因为寻找的
Δ
x
\Delta x
Δx会使L每次都使得L下降,但是cost function F不一定会下降(因为L是对F的二次近似,理论保证是L每次都会下降,但是实际F不一定下降),所以当
ρ
<
0
\rho<0
ρ<0时表示F上升了。
当
ρ
\rho
ρ>1时代表此时方向是正确的,则应减小
μ
\mu
μ加快下降速度;如果0<
ρ
\rho
ρ<1则代表则代表实际下降比较小,可能已经到最优值附近,应增大
μ
\mu
μ减慢下降速度。
Δ x \Delta x Δx越小说明近似的越好,越接近最优值。

发现了14讲关于这个
μ
\mu
μ更新策略的一个错误,
ρ
>
3
4
\rho>\frac{3}{4}
ρ>43时应该减小阻尼
μ
\mu
μ,
ρ
<
1
4
\rho<\frac{1}{4}
ρ<41时应该增大阻尼
μ
\mu
μ
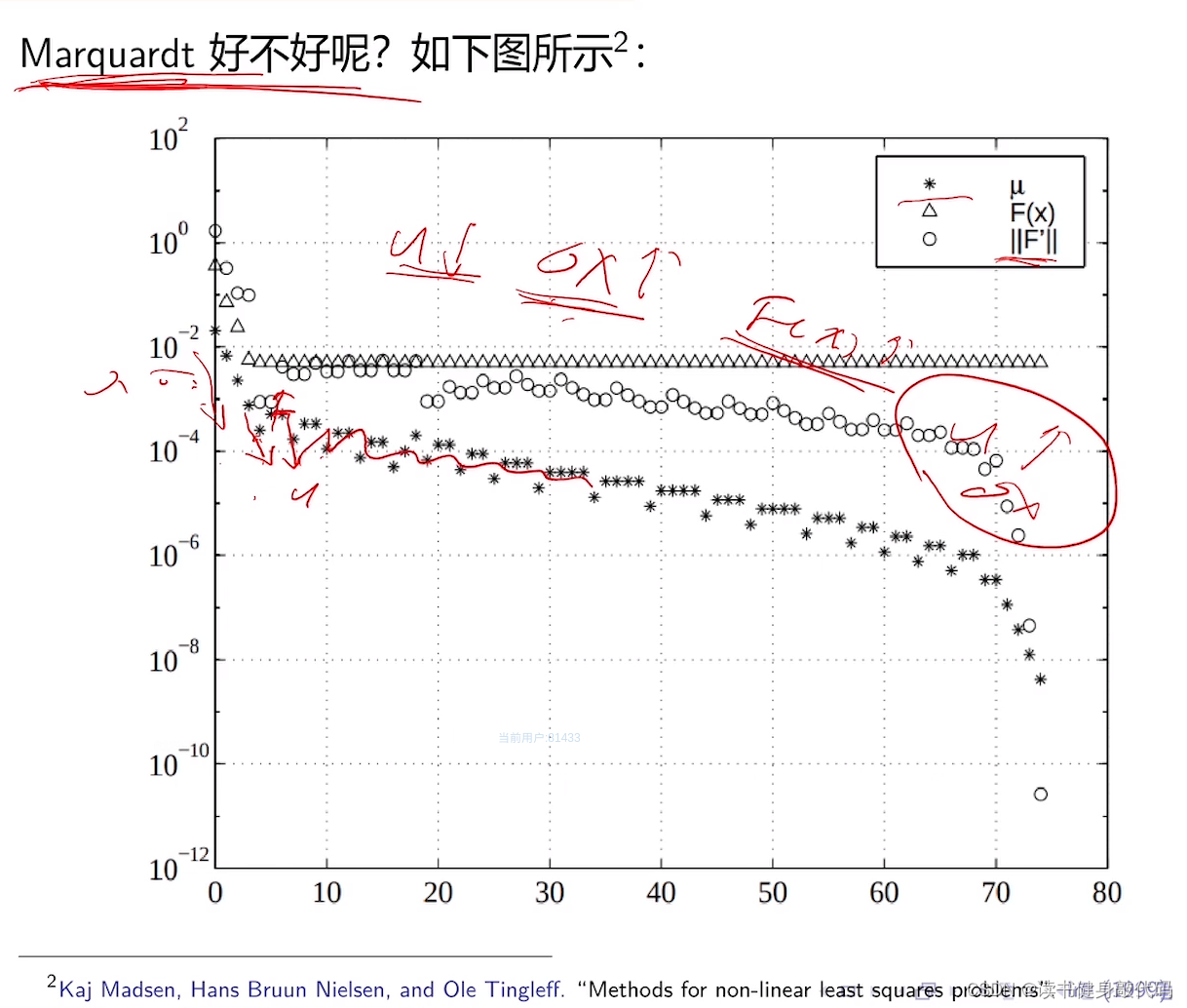
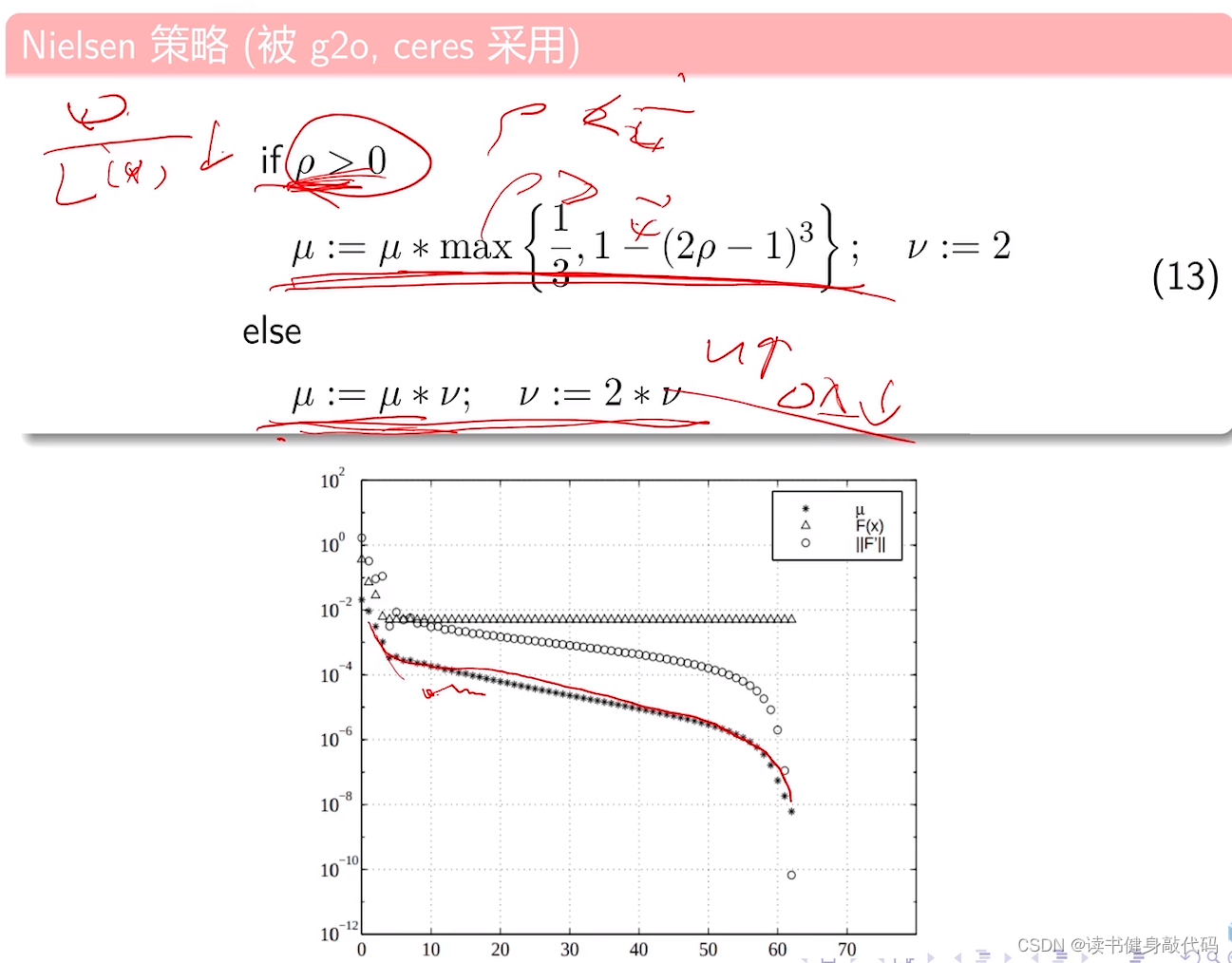
Nielsen采用了新的
ρ
\rho
ρ的计算策略,分母直接为L,判断
ρ
\rho
ρ的符号,当F下降时逐渐减小
ρ
\rho
ρ,当增大时,
ρ
\rho
ρ下降的也很快。
2.3 鲁棒核函数(或叫M-Estimation)
outlier会使得F变得很大,为了处理outlier,在
f
2
f^2
f2外面增加一层
ρ
\rho
ρ对f进行处理
ρ
(
f
2
)
\rho(f^2)
ρ(f2),也有
ρ
(
f
)
2
\rho(f)^2
ρ(f)2

给x微小扰动
Δ
x
\Delta x
Δx计算
Δ
s
\Delta s
Δs,带入(14)可得加上鲁棒核函数之后的展开式


鲁棒核函数本质上是对每项误差的重加权(Reweighted),State Estimation中有对Iterated Reweighted Least Square(IRLS)和鲁棒核函数等价的证明。

95%有效原则,带上outlier和不带时的协方差之比接近95%, 原文较接近数理统计方面的东西。
- 对正态分布,若鲁棒核是Huber,则控制参数设为1.345可满足95%原则,Cauchy应为2.3849
- 若非正态分布,则需统计残差协方差,在进行归一化处理(SVO,DVO,PTAM都是如此)变成正态分布,然后在使用正态分布的参数处理方法。
(但是在实际可能这个参数不会影响很大,可能直接设置为1,大多数情况Cauchy更好,可以证明Cauchy核函数等价于IRLS,但是Huber是线性的,更简单,Cauchy对每个残差要多算个log)
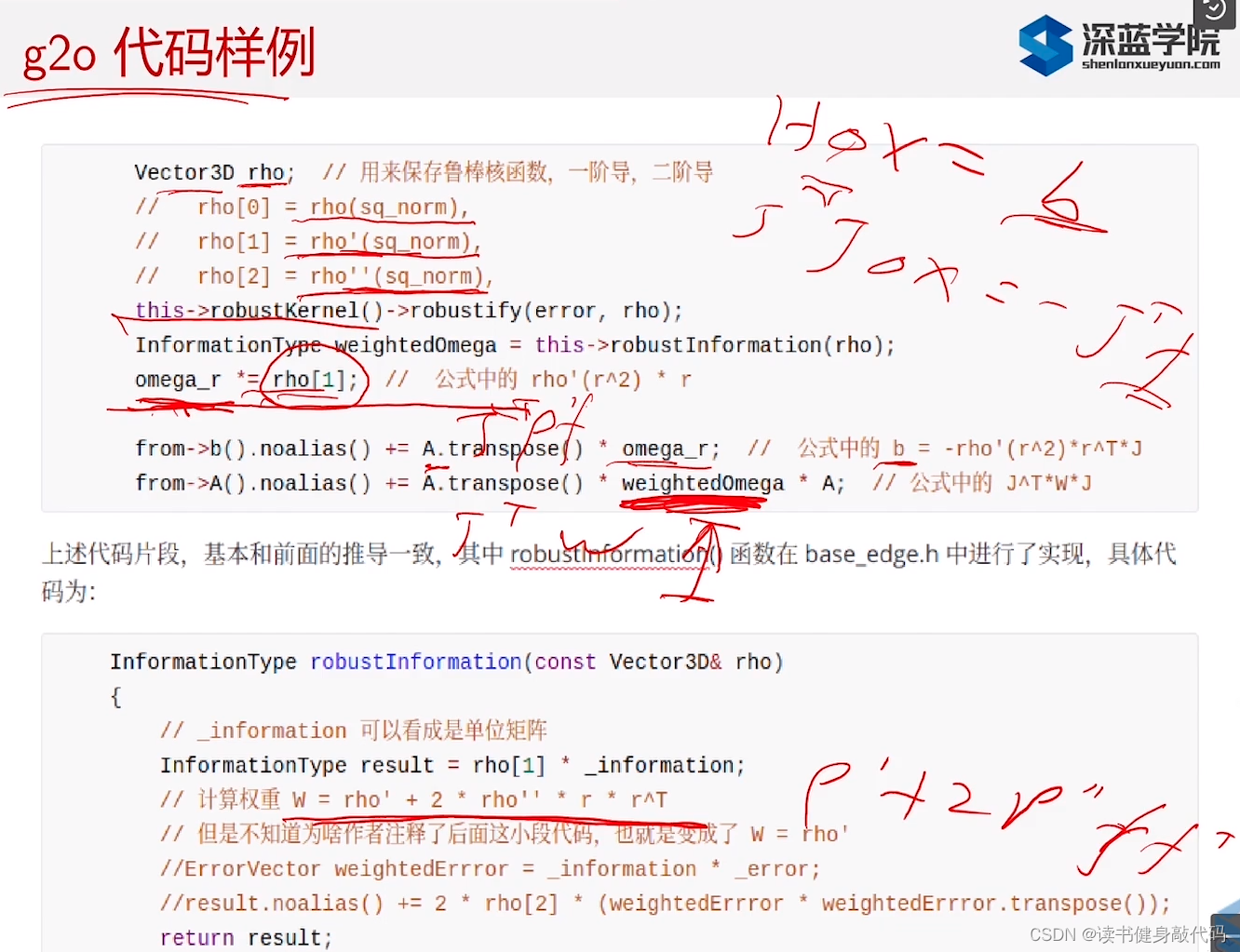
g2o里面残差的一二阶导数应该可以和前面的对应起来了

2.4 小结:

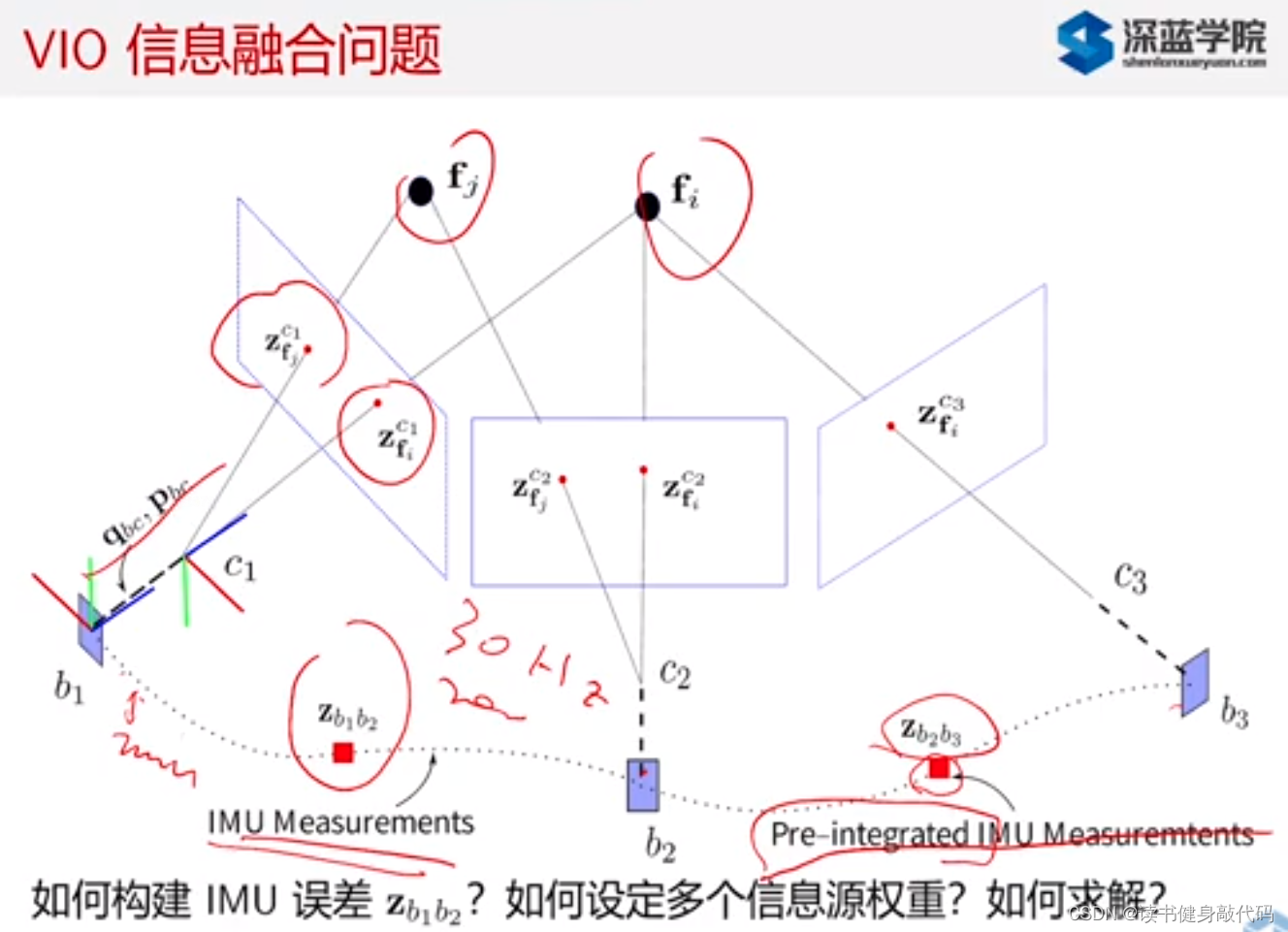
3. VIO残差函数的构建
3.1 IMU预积分
- 从归一化残差的角度来考虑信息矩阵 Σ − 1 \Sigma^{-1} Σ−1,为了把不通传感器的误差进行归一化,然后叠加使用,中间用信息矩阵进行了重加权。
- 从优化的角度来理解信息矩阵,残差f(x)小,协方差小,逆就大,所以应该占的权重更大,更关注这些准确的点。
基于滑动窗口的VIO残差的构建。
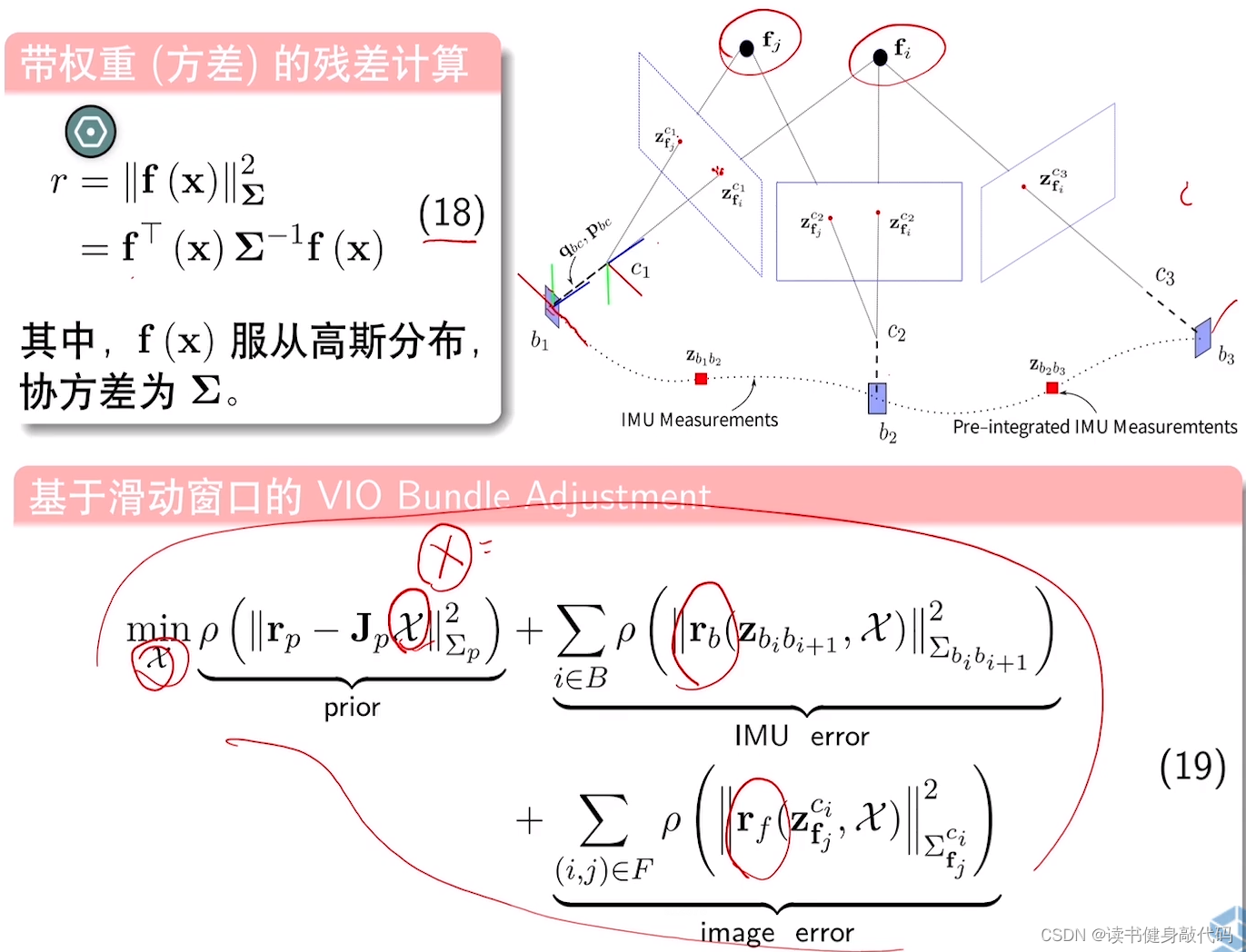
上述
第一项prior代表之前时刻的先验,
第二项代表当前窗口内数据的残差,因为之前之前窗口外时刻的观测数据可能还有用,所以当做先验加入优化项中进行优化,
第三项是我们熟悉的相机的误差(如重投影误差)
关于IMU需要优化的状态量:

其中
λ
\lambda
λ是逆深度(不知道为什么要在这里加入到残差中进行优化)
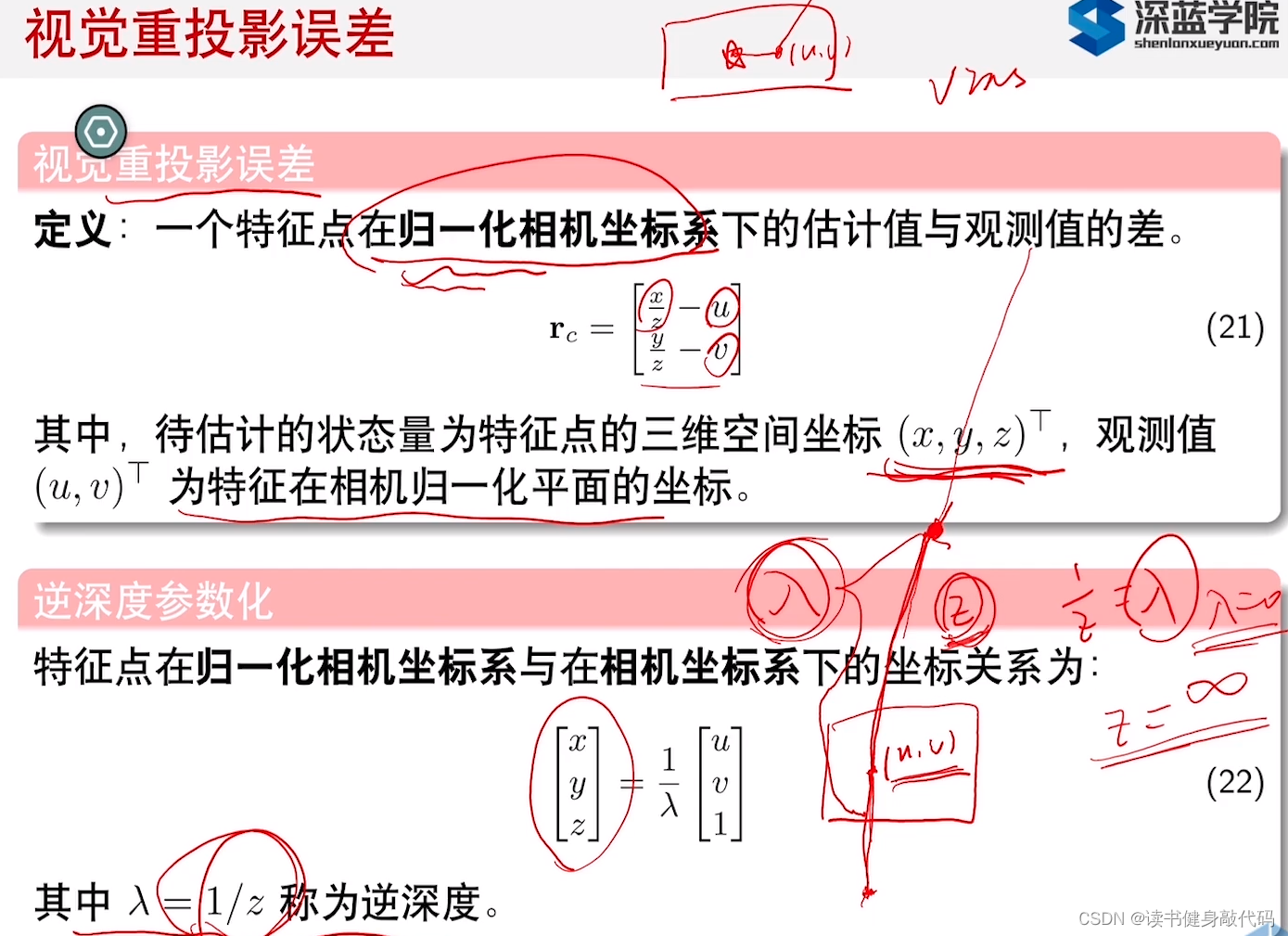
逆深度实际上是另一种参数化方式,类似于(x,y,z),xyz具有相关性,体现在协方差矩阵上,非对角线元素不为0,而u,v,d,可以近似独立,所以协方差矩阵可为对角阵。实际上d不为正态分布,但是1/d可近似为正态分布。(具体描述见SLAM14将建图的P326)
误差的构建:
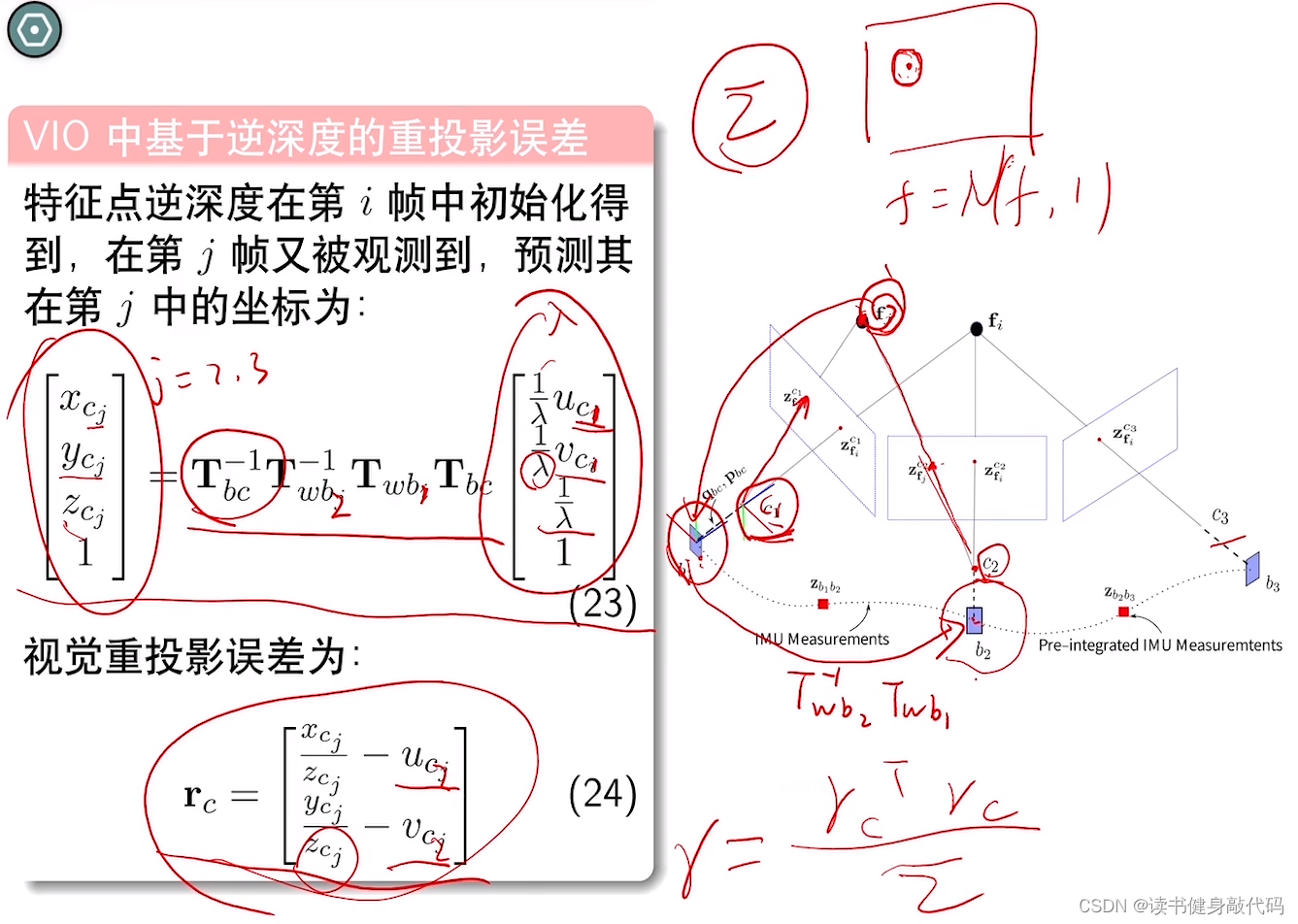
基于逆深度的rpj误差

加速度积分,速度积分,旋转四元数积分:
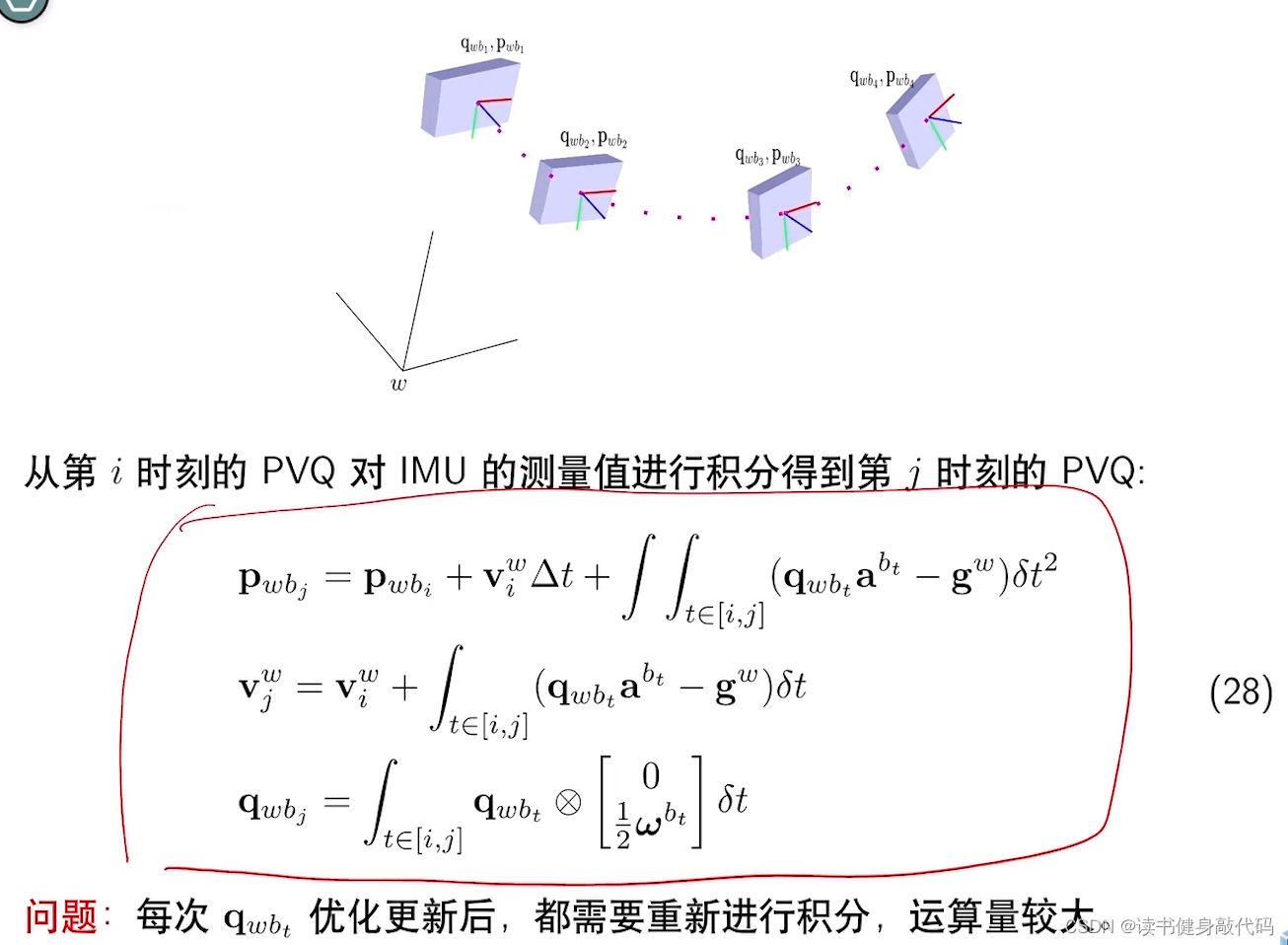
每次前面的数据如果变化的话,后面的所有的值都要跟着积分变化,计算量很大。
把100个积分变成一个就好了,于是出现了IMU预积分:
预积分思想是:把相对于世界坐标系的单领出来,IMU各个时刻之间的相对位置不变(这部分就叫做IMU预积分)


将(32)式中的右边移项得到
α
(
位移
)
,
β
∗
(
速度
)
\alpha(位移),\beta*(速度)
α(位移),β∗(速度)的预测值,和观测值作差即得IMU预积分的误差,bias直接两时刻的测量相减即可,四元数旋转需要按照下面的推导来计算。

回顾第一讲中关于四元数的求导
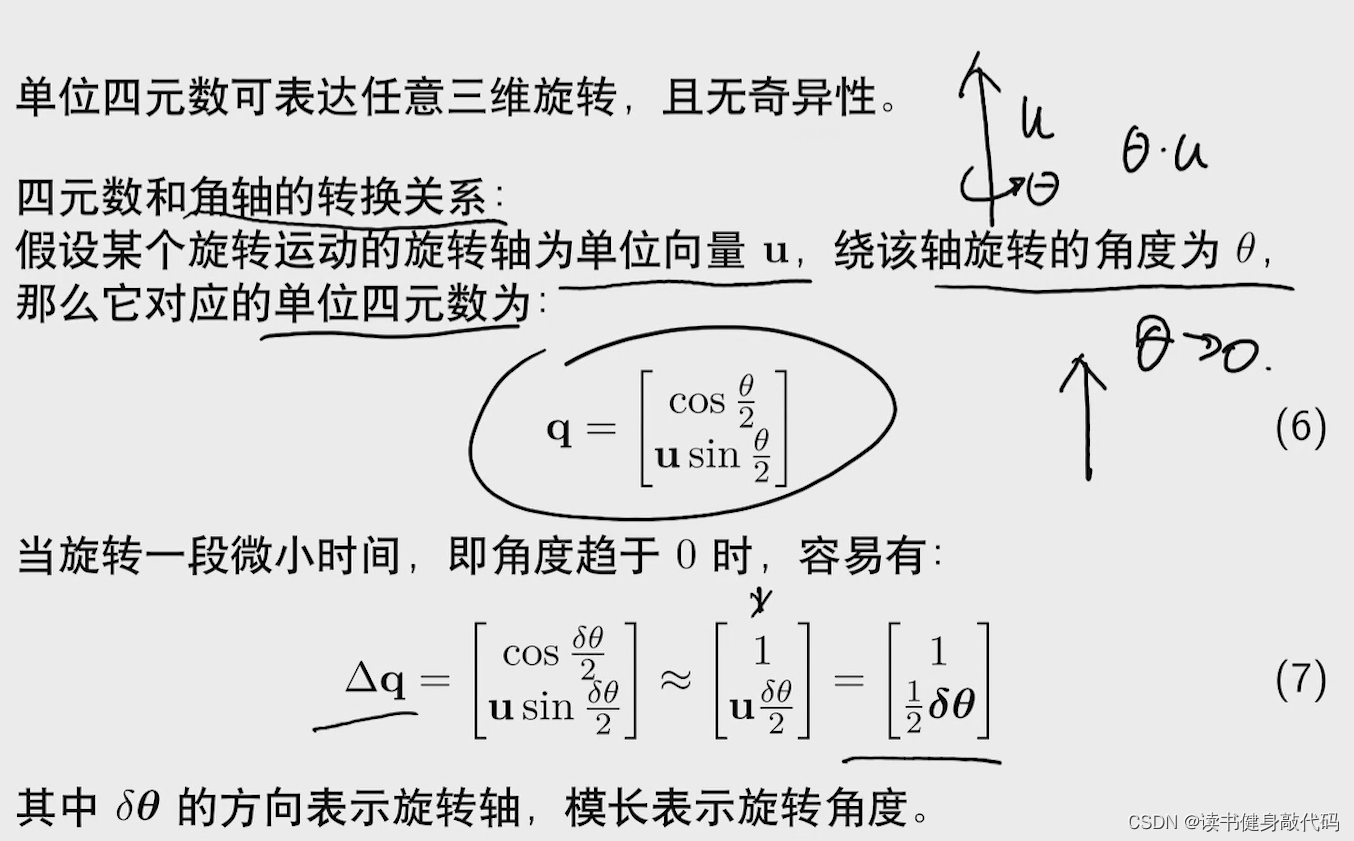
虚部取出来
θ
2
\frac{\theta}{2}
2θ ,乘以2就得到了旋转的角度
θ
\theta
θ
3.2 预积分的离散形式

3.3 预积分的方差传递
一个IMU数据的协方差和不确定度可以标定出来,但是如何传递呢?


3.4 状态误差线性化
两种方法:
- 将误差一阶泰勒展开,
- 求出误差的一阶导数,进行传递

KF假设马尔科夫性,k时刻的数据只和k-1有关,KF只能用于线性系统,若想拓展到非线性系统,则可以将运动和观测方程在某点一阶泰勒展开,只考虑线性部分,就得到了EKF(见SLAM14讲后端1部分)。下面真值等于后验+误差? 一阶泰勒展开,两边消去真值就得到了状态误差的传递


因为已知速度和状态量之间的关系,所以求其误差之间的关系也是可以的,所以会有第二种基于误差的一阶导数的方法,常见于MSCKF这类优化的论文中。

而基于优化的方法(VISN-mono,预积分等)中大多数使用的是第一种基于一阶泰勒展开的方法:
3.5 预积分误差的雅克比推导
总体思想是:位置,速度,角度,加速度,角速度都会受到各种测量噪声的影响,比如角度测量可能会受到一个旋转的影响,所以加上一个小的旋转的扰动就能求角度的雅克比。
分别是角速度,旋转四元数,加速度,预计分量:
α
,
β
\alpha,\beta
α,β,以及加计和陀螺的bias




对各状态量求导:
3.5.1 对速度预计分量的雅克比
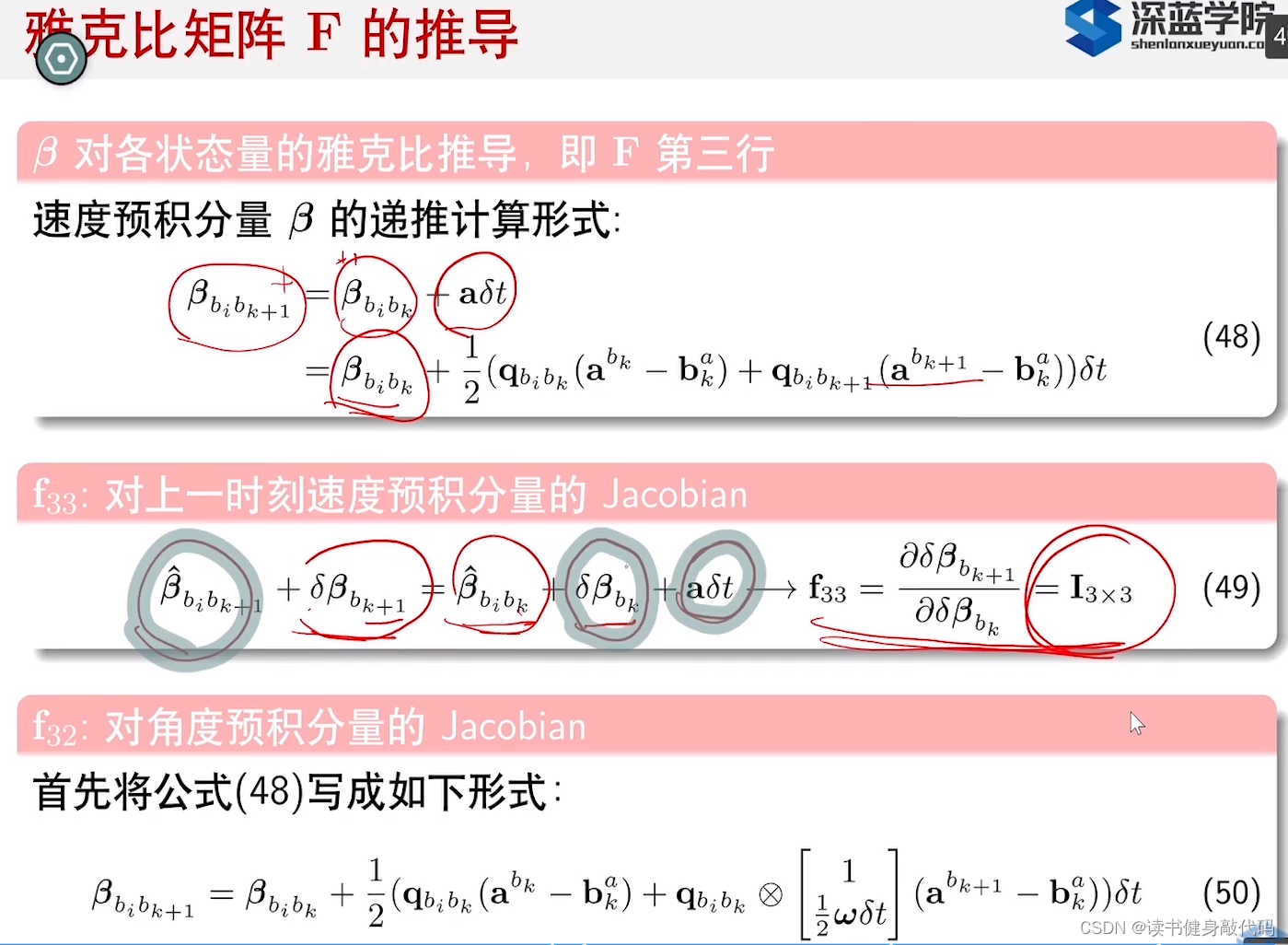
上面的(49)是(48)两边
β
\beta
β一阶泰勒展开,然后右边对
β
b
k
\beta_{b_k}
βbk求偏导,即得对上一时刻速度预计分量(
β
b
k
\beta_{b_k}
βbk)的雅克比。
3.5.2 对角度预计分量的雅克比

k时刻旋转会受到一个微小的旋转扰动(可写成se(3)形式),

对exp进行一阶泰勒展开,再利用反对称矩阵的性质:
a
∧
b
=
−
b
∧
a
a^{\wedge}b=-b^{\wedge}a
a∧b=−b∧a即可约掉分母,得part1的雅克比。

所以可得对角度预积分量的雅克比
f
32
f_{32}
f32
part2这部分我看不太懂(可能是有公式)
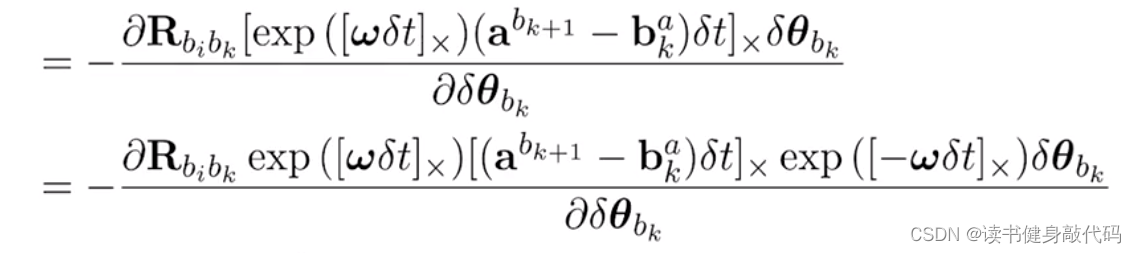
3.5.3 速度预计分量对角速度bias的雅克比

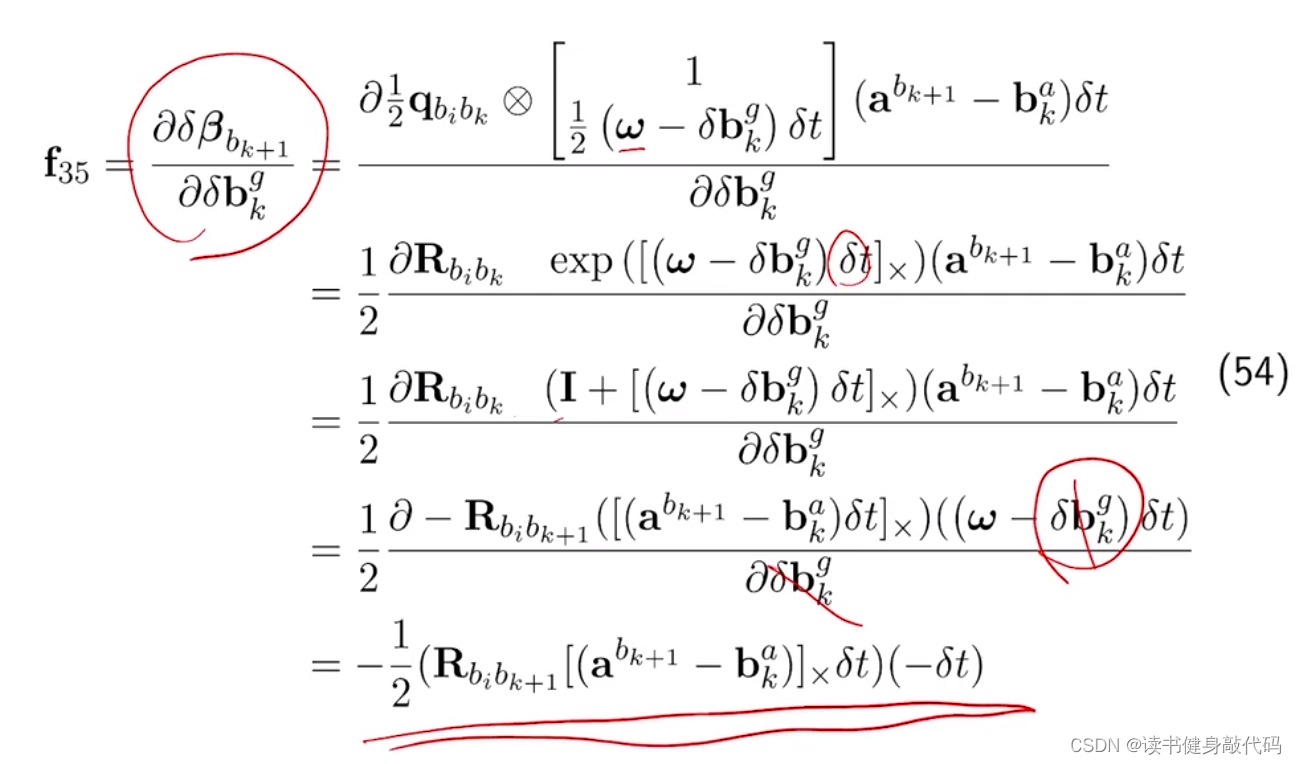
为什么前面的一项跟分母没关系,直接扔掉了?
3.5.4 旋转预积分的递推公式

只考虑旋转误差,不考虑角速度测量的bias等误差,而且四元数有如下性质:
对一个向量进行旋转R相当于对应的四元数左右四元数相乘

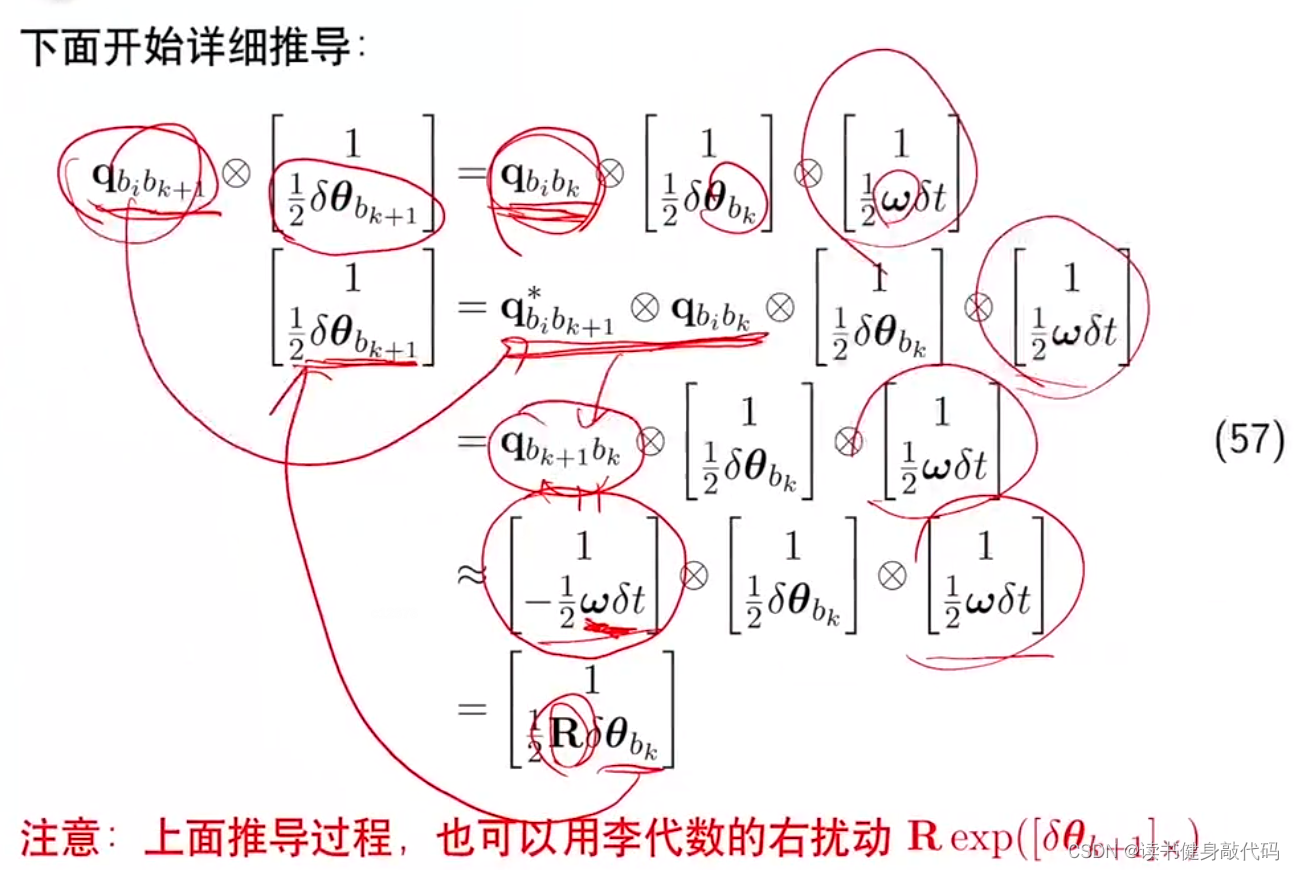
这里把 q b i b k + 1 q_{b_ib_{k+1}} qbibk+1左乘个逆移到右边,计算旋转的测量值的误差传递,倒数第二行就是运用上面的四元数的公式,R就是 [ 1 − 1 2 ω δ t ] \begin{bmatrix} 1 \\ -\frac{1}{2} \omega\delta t \\ \end{bmatrix} [1−21ωδt]对应的旋转矩阵,于是就可以看出,从k到k+1时刻的姿态角的不确定度是通过R矩阵传递的。(还是有些不太明白)

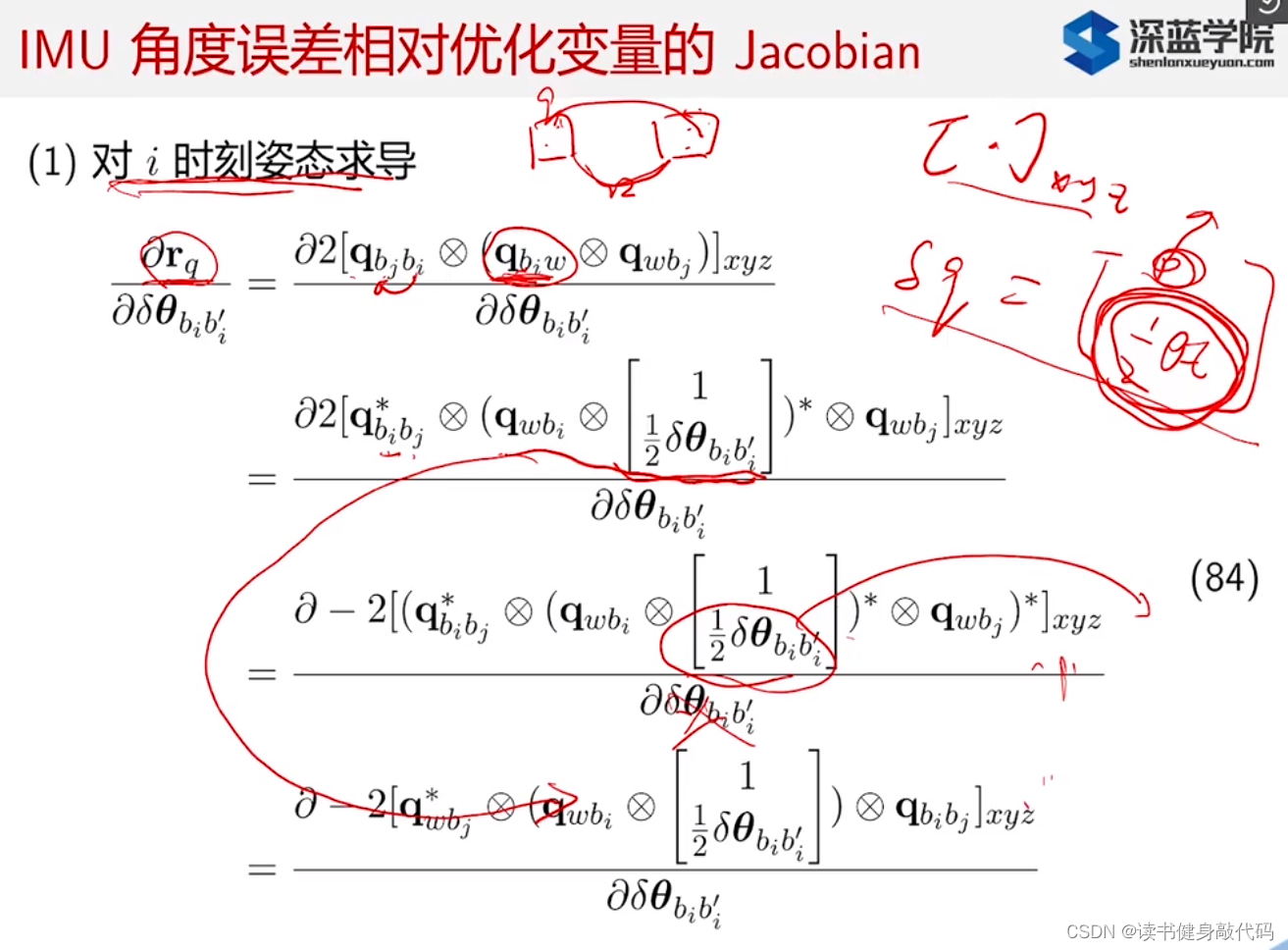
4. 系统Jacobian的推导(自己推一遍,有R的就右乘一个exp然后再换出来,剩下的逆深度等就是链式求导法则)
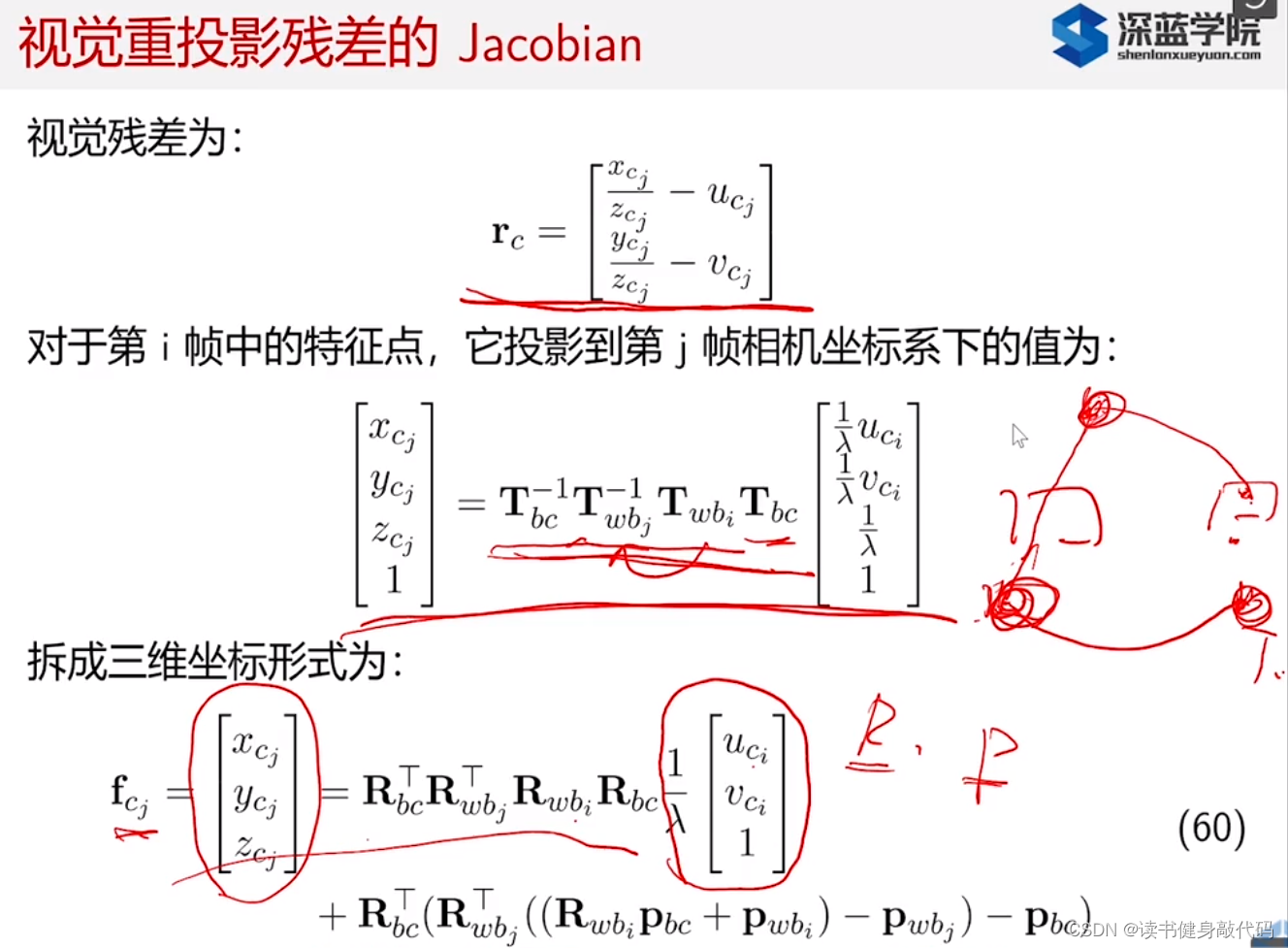





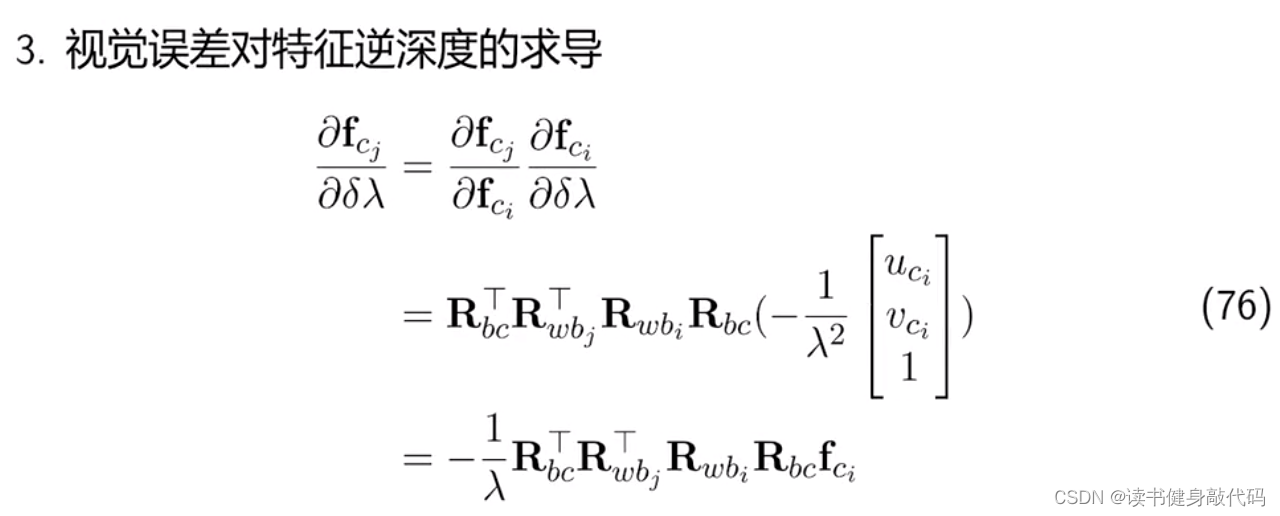

预计分量对bias求导较为麻烦,预积分假设bias不动,但是实际上bias是动的,所以求他的bias就是比较麻烦的(我理解就是因为预积分有bias不动的先验,然后再去推对bias的导数就有些冲突),所以这里就使用了一阶泰勒展开来近似,丢掉高阶项,



4.1 举个例子
姿态对角度求导,IMU预积分得一个
q
j
i
q_{ji}
qji,world系下得两个时刻的q,之间可以求出一个
q
j
i
q_{ji}
qji,求这两个
q
j
i
q_{ji}
qji四元数之间的四元数乘法可得相对位姿,取虚部对角度求导即得Jacobian。方法是对
q
w
b
i
q_wb_i
qwbi取一个小扰动,使用公式变换到右边去,跟分母消掉(下面*都代表取逆),下面还有关于四元数左乘和右乘的算子,看Joan sola的四元数手册。
(高翔说还能用李代数?四元数连乘会麻烦一些,用李代数会简单点?)
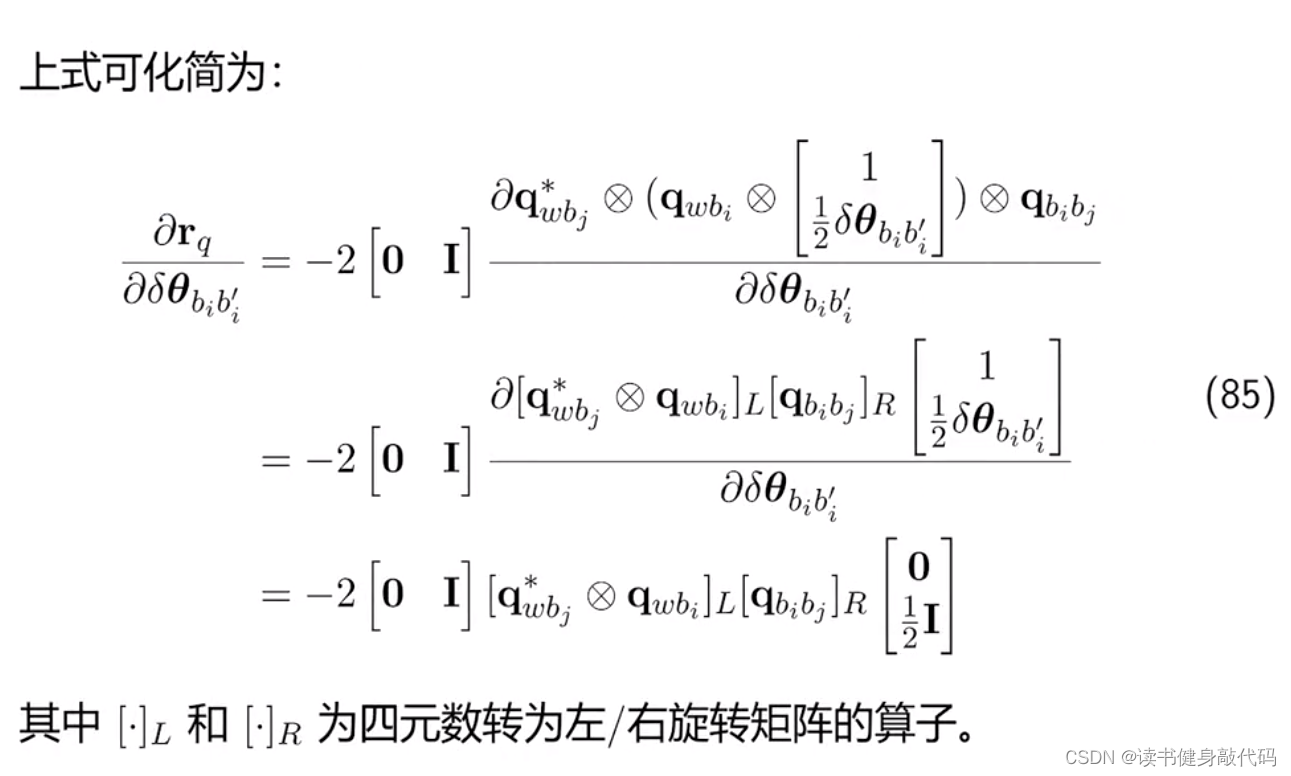


这个下面需要自己推导。
TODO:
预积分误差传递的推导,
整体系统的Jocabian的推导。
5. 作业
详见:我的作业博客。

5. 待读文献
5.1 SBA论文
5.2 LM改进阻尼因子 ρ \rho ρ论文
μ
\mu
μ反复震荡(由于F反复增大和减小,导致要不断调整
μ
\mu
μ)导致浪费了很多计算次数。
最后Nielsen在此文中改进了
ρ
\rho
ρ的更新策略。
5.3 关于鲁邦核函数的论文
3是综述,对4种方法进行了讨论

5.4 鲁棒核函数