今天解读一篇Hinton大佬最近分享的论文。

在最近的NeurIPS2022会议上，图灵奖得主Hinton作为演讲嘉宾，分享了一个题为《The Forward-Forward Algoritm: Some Preliminary  Investigations》的论文。

该论文提出了一种取代反向传播的前向-前向传播的训练方式，引起了不少讨论。

这篇论文大概有两个亮点——

• 使用 Forward-Forward 算法替代 Forward-Backward 算法，摒弃反向传播算法

• 神经网络的软件可以是非“永生的”。

我拜读了这篇论文，并且试着以个人的理解来解读下这篇论文。如有错误，欢迎交流。论文链接：https://www.cs.toronto.edu/~hinton/FFA13.pdf

---

我们都知道，神经网络的训练分为两大步骤——前向传播和反向传播。

前向传播的过程是一种推理计算的过程：给定一个输入数据，从神经网络的第一层开始往后计算，到最后一层，输出一个结果，或完成图像分类，或完成语音翻译。

反向传播的过程，则是在神经网络训练时，计算每次前向传播的结果与真实结果的误差，反向完成一些层的权重（参数）的更新，使得下一次前向传播能比上一次有更好的结果，周而复始，一轮轮的迭代，直到整个网络收敛，神经网络完成训练。

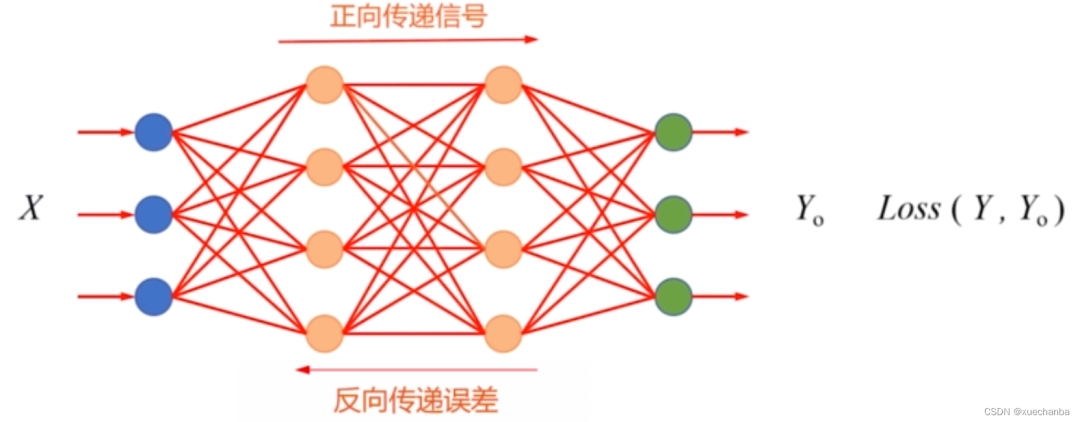
在过去的十几年时间里，深度学习之所以取得了惊人的成就，大都是建立在了海量数据集的训练，以及使用反向传播，基于链式法则的梯度更新这一基础上的。

至少在已有的很多深度学习任务中，这一做法是有效的。

虽然有效，但脑神经科学家们一直对此抱有怀疑态度，甚至反对。

因为目前的科学研究，几乎找不到人类大脑皮层中的神经元，在进行记忆提取或记忆存储时，存在类似反向传播这一过程证据。

也就是说——

反向传播虽然有效，但可能与人脑的记忆走得是不同的路子。

想想也是，人工智能如果想要实现真正的智能，至少应该在顶层设计上，和人脑的机制大概保持一致才行。

这也促使出现了一种声音：反向传播算法作为一种人工智能的学习方式实在令人难以置信。

除此之外，反向传播算法还存在另外一个严重限制：那就是我们需要完全了解前向传播中的算法，才能计算出反向传播时的导数。

这要求前向传播中的算法是可微分的。为什么神经网络训练需要微分，可查看 浅谈自动微分是个啥？

而如果我们在前向传播中插入一个黑盒，但不知道黑盒中的具体算法实现，除非可以学习到这个黑盒的微分模型，否则是不可能完成黑盒的微分的。

基于上述的背景，Hinton的这篇文章，提出了使用 Forward-Forward 算法来代替 Forward-Backward 算法。

显然，是为了避免以上所说的反向传播的限制，或者说创造性的颠覆反向传播算法。

Forward-Forward 算法

这一算法解决的首要问题，便是解除前向传播中算法必须可微这一限制。

它使用前向-前向传播代替前向-反向传播。这两个前向传播计算相同，但是使用的数据集以及最终的目标不同。

一个前向传播称之为 Positive Pass。这个过程对真实的数据（正样本）进行操作，同时调整权值来完成每一层的增益（increase the goodness）。

另一个前向传播称之为 Negative Pass。这个过程对负样本（negative data）进行操作，同时调整权值以完成每一层的减益（decrease the goodness）。

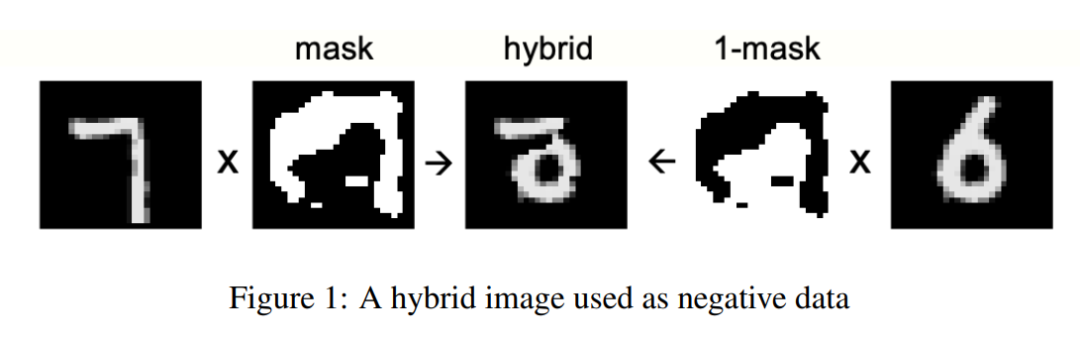
通过这两个前向传播，来完成每一层的权值调整。

这和之前反向传播将误差从最后一层往前传不同：它不需要从最后一层将误差传递过来更新每一层的权值，而是每一层自己使用正负样本的计算来调整权值。

文中，作者使用前向-前向算法对一些常见深度学习任务做了实验，并对比了结果，效果不错。具体细节可以查看原文。

对于这篇论文，其实我更感兴趣的是最后一个章节——一种称之为Mortal Computation 的计算方式。

计算不再“永生”

我觉得这是这篇文章比较有意思的地方，同时这也是 Forward-Forward 算法带来的另一个潜在的好处——

不使用反向传播算法，从而使得原来必须要依赖数字电路完成的运算，可以使用模拟电路来实现。

这一转换能带来更高的能效比提升。

为什么？

因为反向传播过程中，从最后一层反传时的误差有时会很小，对数值的精度要求要比单纯的前向传播更高。

而模拟计算一般很难达到这么高的精度。

这就要求在依靠反向传播进行神经网络的训练中，使用的硬件需要额外加一个AD转换（模拟到数字的转换）电路，将模拟信号转换为数字信号，然后完成计算。

而 Forward-Forward 算法既然摒弃了反向传播，那自然也不需要AD转换了，从而只需要使用模拟运算就可以完成需要的训练任务。

在数字电路运算中，如果要计算两个n-bit的数字相乘，晶体管需要使能电压的高低来表示 n 个 bit 位，从而代表某个 n-bit 的数字，在使用晶体管高低电平来完成一个 n-bit 数字乘以另一个 n-bit 数字的运算时，消耗大概是O(N^2)的复杂度。

而模拟计算则不需要，对于神经网络常见的运算，比如一个向量乘以矩阵，模拟计算大概可以使用电压来表示一个激活的向量，使用电导来表示权值矩阵（神经网络的参数），而在每个单位运算时间内，他们的乘积结果会直接反映在自身的电压上(add themselves）。

在解除了对数字电路的依赖之后，神经网络的训练过程便可以达到一个更高效的能效比。

打个不恰当的比方，原来训练一个神经网络可能需要消耗1kw 的电能，采用模拟电路来运算之后，可能仅仅只需要消耗1w的电能。

这些优势，都是因为 Forward-Forward 算法摒弃了反向传播带来的。

在文章最后，Hinton 提出了一个更加具有前瞻性的观点——

未来的神经网络计算可能会脱离现在软硬件分离的架构，来实现一种“非永生”的计算模式。

非永生？先了解下什么是“永生”计算——

现在的软件和硬件设计，通常意义上是分离的。

比如写好了一个微信程序，可以运行在小米手机上，底层支持的硬件便是小米手机的Soc（system on chip, 片上系统）和芯片。

突然有一天小米手机摔坏了，难道写的微信程序就不能用了么？

当然不是，换一个华为手机同样能用——

软件和硬件分离，软件不依赖硬件，硬件即使坏了，软件同样还有生命力。

这就是软件永生，这也是现在主流的软硬件设计思路，也是现代计算机科学的基石。

对应到深度学习任务中，神经网络学到的权值就是永生的。我们可以将权值部署到多种硬件上，只要该硬件支持这种计算，那就可以完成相应的推理任务。

权值不随着硬件的消亡而消亡！

而 Hinton 大佬则说，为了有更出色的能效和训练性能，我们大概可以针对某一个特定的硬件进行神经网络的训练，使得该硬件同样可以出色的完成一个特定的深度学习任务，这个硬件会自己学习一些参数，而这些参数与这个硬件绑定。

如此一来，一旦硬件损坏，参数也就不可用，软件死掉，不再"永生"。

如果你希望你的千亿参数量的神经网络在只有几瓦的能耗下就可以工作，软硬件绑定的算法计算或许是唯一的选择。

If you want your trillion parameter neural net to only consume a few watts, mortal computation may be the only option.

文章最后，Hinton当然也说到了，Forward-Forward 算法目前也只是刚刚开始，是一个初步的尝试，未来还有很多的工作要做。更多细节可查看原文阅读。

写在最后

本篇论文除了使用两个前向传播来代替前向和反向传播的训练模式之外，个人感觉文章最后提出的Mortal Computation是亮点。

抛开技术实现难度不谈，人脑的记忆其实就是因人而异，独自训练的。而人脑实时处理海量的数据，消耗的能量也不过几瓦，远远小于目前神经网络模型运行所需要的能耗。

人脑确实是一个精密的组织，虽然现在科学家对人脑的研究也还不成熟，还有很多未解之谜，但伴随着人工智能和神经学家的一起研究，相信未来肯定会有更多的奥秘被解开。

论文预印版可扫描下方WX公号，回复 FF 下载阅读。