基于MATLAB的dijkstra算法

%姓名：马伟
%日期：2023年6月七号
%作业：通信网理论，最小路径树D算法
function [distances, paths, tree] = dijkstra(graph, startNode)
    numNodes = size(graph, 1);
    distances = inf(1, numNodes);
    visited = false(1, numNodes);
    previous = zeros(1, numNodes);

    distances(startNode) = 0;
    tree = cell(1, numNodes);

    while sum(visited) < numNodes
        minDistance = inf;
        currentNode = -1;

        for node = 1:numNodes
            if ~visited(node) && distances(node) < minDistance
                minDistance = distances(node);
                currentNode = node;
            end
        end

        if currentNode == -1
            break;
        end

        visited(currentNode) = true;

        for neighbor = 1:numNodes
            if graph(currentNode, neighbor) > 0 && graph(currentNode, neighbor) ~= inf
                newDistance = distances(currentNode) + graph(currentNode, neighbor);
                if newDistance < distances(neighbor)
                    distances(neighbor) = newDistance;
                    previous(neighbor) = currentNode;
                    % 记录树边
                    tree{neighbor} = [currentNode, neighbor];
                end
            end
        end
    end

    paths = cell(1, numNodes);
    for i = 1:numNodes
        paths{i} = reconstructPath(previous, i);
    end
end

function path = reconstructPath(previous, endNode)
    path = [];
    currentNode = endNode;
    while currentNode ~= 0
        path = [currentNode, path];
        currentNode = previous(currentNode);
    end
end

测试代码


clc;
clear all;
% 邻接矩阵
graph = [0 9 1 3 inf inf;
         1 0 4 inf 7 inf;
         2 inf 0 inf 1 inf;
         inf inf 5 0 2 7;
         inf 6 2 8 0 5;
         7 inf 2 inf 2 0];


numNodes = size(graph, 1);
startNode = 1;
% 运行 Dijkstra 算法
[distances, paths, tree] = dijkstra(graph, startNode);

% 构建边列表和权重列表
% 构建边列表和权重列表
edges = [];
weights = [];
for i = 1:numNodes
    if ~isempty(tree{i})
        edges = [edges; tree{i}];
        weights = [weights; graph(tree{i}(1), tree{i}(2))];
    end
end

% 创建有向图对象
g = digraph(edges(:, 1), edges(:, 2));

% 绘制图形
figure ;
h = plot(g, 'Layout', 'layered');
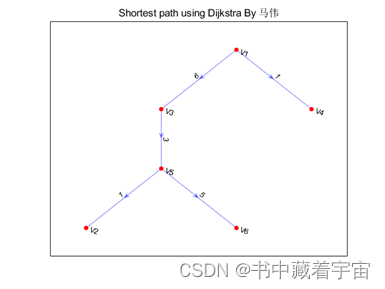
title("Shortest path using Dijkstra By 马伟")

% 设置节点和边的标签
nodeLabels = cellstr(num2str((1:numNodes)', 'V%d'));
h.NodeLabel = nodeLabels;
h.EdgeLabel = cellstr(num2str(weights, '%g'));

% 设置节点和边的颜色
h.NodeColor = 'r';
h.EdgeColor = 'b';

% 显示最短路径和迭代过程中的节点情况
disp('V1节点到各个节点的最短路径:');
disp('迭代过程中的节点情况如下所示:');
for i = 1:numNodes
    disp("------------------------------")
    disp(['{ V', num2str(startNode),' }', ' 到 { V', num2str(i), ' }',':']);
    disp(['路过的节点为: ', num2str(paths{i})]);
    disp(['总体权重: ', num2str(distances(i))]);
 

end
%系统画图（原图）-------------------------------------
% 创建有向图对象
G = digraph(graph, 'omitselfloops');

% 绘制连通图
figure;
h = plot(G, 'Layout', 'layered');
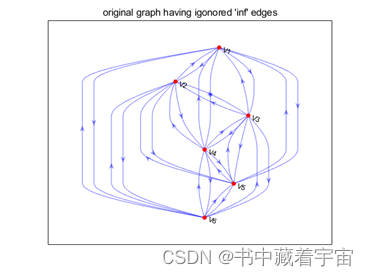
title("original graph having igonored 'inf' edges")
% 设置节点和边的标签
numNodes = size(graph, 1);
nodeLabels = cellstr(num2str((1:numNodes)', 'V%d'));
h.NodeLabel = nodeLabels;

% 设置节点和边的颜色
h.NodeColor = 'r';
h.EdgeColor = 'b';


%系统画图（最小路径树）-------------------------------------

% 创建有向图对象
G = digraph(graph, 'omitselfloops');

% 计算从 V1 节点到其他节点的最短路径
startNode = 1;
numNodes = size(graph, 1);
shortestPaths = cell(1, numNodes);
for i = 1:numNodes
    shortestPaths{i} = shortestpath(G, startNode, i);
end

% 构建最小路径树的边列表
edges = zeros(0, 2);
for i = 1:numNodes
    path = shortestPaths{i};
    for j = 1:length(path) - 1
        % 只添加从 V1 节点到其他节点的最短路径中的边
        if ~ismember([path(j), path(j + 1)], edges, 'rows')
            edges = [edges; path(j), path(j + 1)];
        end
    end
end

% 创建最小路径树的有向图对象
tree = digraph(edges(:, 1), edges(:, 2));

% 绘制最小路径树
figure;
h = plot(tree, 'Layout', 'layered');
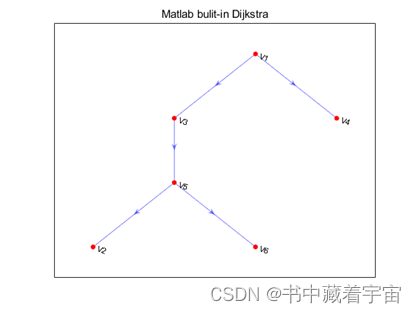
title("Matlab bulit-in Dijkstra")
% 设置节点和边的标签
nodeLabels = cellstr(num2str((1:numNodes)', 'V%d'));
h.NodeLabel = nodeLabels;

% 设置节点和边的颜色
h.NodeColor = 'r';
h.EdgeColor = 'b';