【半监督医学图像分割 2023 CVPR】BCP

论文题目：Bidirectional Copy-Paste for Semi-Supervised Medical Image Segmentation

中文题目：双向复制粘贴半监督医学图像分割

论文链接：https://arxiv.org/abs/2305.00673

论文代码：https://github.com/DeepMed-Lab-ECNU/BCP

论文团队：华东师范大学&上海交通大学

发表时间：2023年5月

DOI:

引用：

引用数：

摘要

在半监督的医学图像分割中，存在着有标签和无标签数据分布的经验不匹配问题。如果将有标记的数据和无标记的数据分开处理或以不一致的方式处理，那么从有标记的数据中学到的知识可能在很大程度上被丢弃。

我们提出了一个直接的方法来缓解这个问题–在一个简单的Mean Teacher架构中，双向复制粘贴有标签的和无标签的数据。该方法鼓励未标注的数据从标注的数据中向内和向外学习全面的共同语义。

更重要的是，标记数据和未标记数据的一致学习程序可以在很大程度上减少经验分布差距。详细来说，我们将已标记的图像（前景）的随机裁剪复制到未标记的图像（背景）上，并将未标记的图像（前景）复制到已标记的图像（背景）上，分别。

这两张混合图像被送入一个学生网络，并由伪标签和地面真相的混合监督信号进行监督。我们发现，在有标签和无标签的数据之间双向复制粘贴的简单机制已经足够好了，而且实验显示，与其他半监督医学图像分割数据集的先进技术相比，有了实实在在的收获（例如，在ACDC数据集上有超过21%的Dice改善，有5%的标签数据）。

1. 简介

从计算机断层扫描（CT）或磁共振成像（MRI）等医学图像中分割内部结构对许多临床应用来说是至关重要的[34]。各种基于监督学习的医学图像分割技术已经被提出[4,13,45]，这通常需要大量的标记数据。但是，由于在标注医学图像时，人工勾画的过程繁琐而昂贵，近年来，半监督分割吸引了更多的关注，并在医学图像分析领域变得无处不在。

一般来说，在半监督医学图像分割中，标记数据和未标记数据是从相同的分布中提取的（图1(a))。 但在实际场景中，由于标记数据的数量很少，很难从标记数据中估计精确的分布。 因此，在大量未标记数据和极少量标记数据之间总是存在经验分布不匹配[30]（图1(b)和©)。 半监督分割方法总是试图以一致的方式对称地训练标记和未标记的数据。 例如，自训练[1，48]生成伪标签，以伪监督的方式监督未标记的数据。 Mean基于教师的方法[40]采用一致性损失来“监督”具有强增强的未标记数据，类似于监督具有基本真相的标记数据。 DTC[16]提出了一个双任务一致性框架，适用于标记数据和未标记数据。 ContrastMask[31]在标记和未标记的数据上应用密集对比学习。 但是现有的大多数半监督方法都是在不同的学习范式下使用有标记和无标记的数据。 因此，它往往导致从标记数据中学习到的大量知识被丢弃，以及标记数据和未标记数据之间的经验分布不匹配（图1(e))。

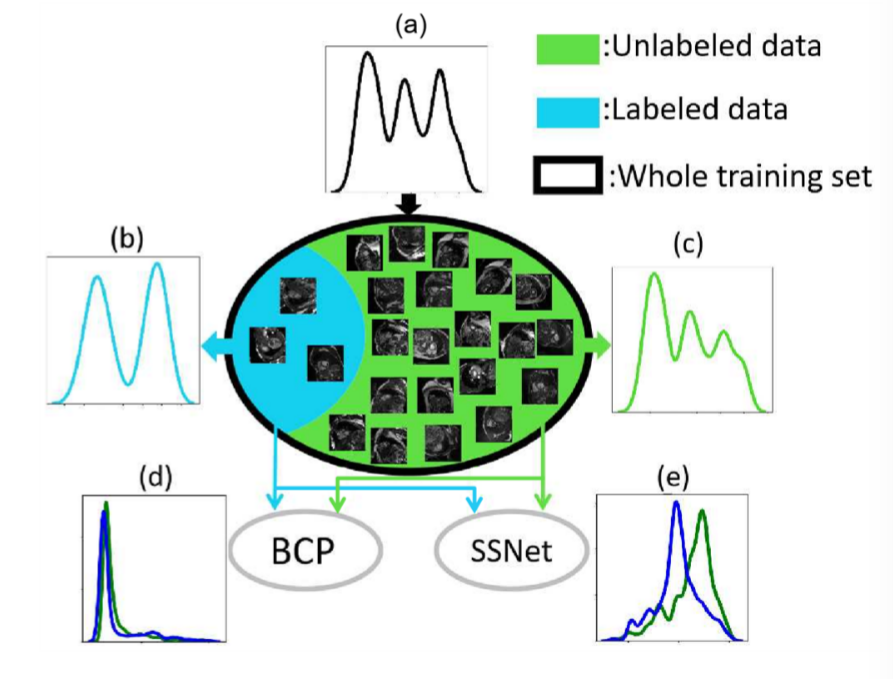
图1. 半监督倾斜设置下的不匹配问题的说明。假设训练集是从（a）中的潜在分布中提取的。但是少量标注数据和大量未标注数据的经验分布分别是（b）和（c）。使用少量的标签数据来构建整个数据集的精确分布是很难的。(d) 通过使用我们的BCP，标记的和未标记的特征的经验分布是一致的。(e) 但其他方法，如SSNet[35]或交叉无标签数据复制粘贴，不能解决经验分布不匹配的问题。所有分布都是ACDC[2]中属于心肌类的体细胞的核密度估计。

CutMix[42]是一种简单而强大的数据处理方法，也被称为复制粘贴(CP)，它有可能鼓励未标记的数据从标记的数据中学习共同的语义，因为同一地图中的像素共享更接近的语义[29]。 在半监督学习中，强迫未标记数据的弱-强增强对之间的一致性被广泛使用[11,14,32,47]，而CP通常被用作强增强。 但是现有的CP方法只考虑CP交叉未标记数据[8,10,14]，或者简单地从标记数据中复制作物作为前景并粘贴到另一个数据[6,9]。 它们忽略了为标记数据和未标记数据设计一致的学习策略，从而阻碍了其在减小分布差距方面的应用。 同时，CP试图通过增加无标记数据的多样性来增强网络的泛化能力，但由于剪切混合图像只能由低精度的伪标记来监督，因此很难获得较高的性能。 使用更精确的监督来帮助网络分割由CP切割的退化区域是直观的。

---

为了缓解有标签数据和无标签数据之间的经验不匹配问题，一个成功的设计是鼓励无标签数据从有标签数据中学习全面的共同语义，同时，通过有标签数据和无标签数据的一致学习策略，进一步实现分布的一致性。

我们通过提出一个令人惊讶的简单但非常有效的双向复制-粘贴（BCP）方法来实现这一目标，该方法在Mean Teacher框架中被实例化。

具体来说，为了训练学生网络，我们通过复制粘贴标签图像（前景）上的随机作物到无标签图像（背景）上，以及反过来，复制粘贴无标签图像（前景）上的随机作物到有标签图像（背景）上来增加我们的输入。

学生网络通过教师网络的未标记图像的伪标签和已标记图像的标签图之间的双向复制，由生成的监督信号进行监督。

这两张混合图像有助于网络双向和对称地学习有标签和无标签的数据之间的共同语义。我们根据最先进的技术和我们的方法所训练的模型，计算了来自LA数据集[39]的有标签和无标签的训练集的Dice分数，如图2所示。以前的模型分别处理有标签的数据和无标签的数据，在有标签的数据和无标签的数据之间存在很大的性能差距。例如，MC-Net对有标签的数据获得95.59%的Dice，但对无标签的数据只有87.63%。这意味着以前的模型很好地吸收了来自地面事实的知识，但在转移到无标签数据时却抛弃了很多。我们的方法可以在很大程度上减少有标签数据和无标签数据之间的差距（图1(d)），就其性能而言。同样有趣的是，我们的BCP对有标签数据的Dice比其他方法低，这意味着BCP可以在一定程度上缓解过度拟合的问题。

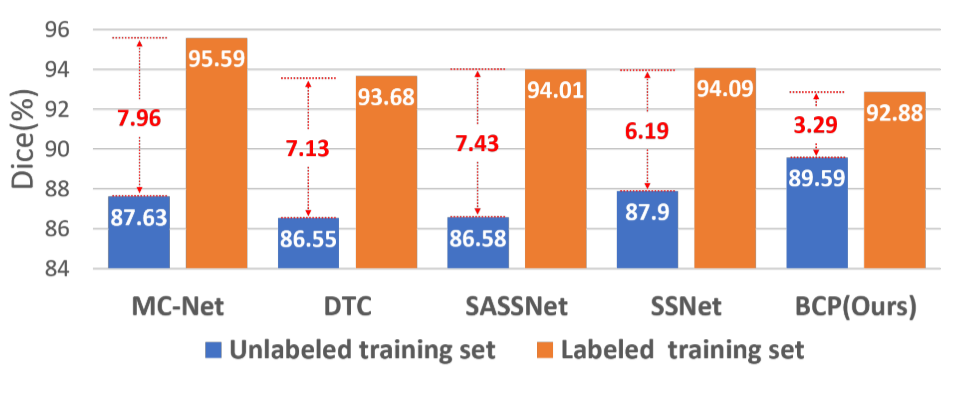
图2。 LA数据集上不同模型的未标记和标记训练数据的Dice分数[39]。 在我们的方法中观察到一个更小的性能差距。

我们在三个流行的数据集:LA[39]，胰腺-NIH[21]和ACDC[2]中验证了BCP。 大量的实验表明，我们的简单方法在ACDC数据集上有5%的标记数据，在骰子方面的改进甚至超过了21%。 烧蚀研究进一步显示了每个提出模块的有效性。 请注意，与基线（例如VNET或UNET）相比，我们的方法没有引入新的训练参数，同时保持相同的计算成本。

2. 相关工作

2.1 医学图像分割

从医学图像中分割内部结构对于许多临床应用是必不可少的[34]。 现有的医学图像分割方法可以分为两类。 第一类设计了各种2D/3D分割网络体系结构[3,4,13,18,20,49]。 第二类利用医学先验知识进行网络培训[23,28,33,38]。

2.2 半监督医学图像分割

在半监督医学图像分割方面，人们做出了许多努力。 熵最小化(EM)和一致性正则化(CR)是两种应用广泛的损失函数。 同时，许多研究都以不同的方式扩展了Mean教师框架。 SASSNET[12]利用未标记的数据对分段输出实施几何形状约束。 DTC[16]通过显式构建任务级正则化，提出了一个双任务一致性框架。 SIMCVD[40]明确地建模了几何结构和语义信息，并将它们约束在教师和学生网络之间。 这些方法使用几何约束来监督网络的输出。 UA-MT[41]利用不确定性信息引导学生网络逐渐从教师网络的有意义和可靠的目标中学习。 [46]结合图像和片状表示来探索更复杂的相似性线索，在给定不同输入大小的情况下使输出保持一致。 Coranet[22]提出了一个模型，该模型可以产生确定区域和不确定区域，学生网络以不同的权重处理教师网络指示的区域。 UMCT[37]利用网络的不同视角预测同一图像的不同视角。 它利用预测值和相应的不确定性生成伪标签，用于监督未标记图像的预测。 这些方法提高了半视觉医学图像分割的有效性。 但是，他们忽略了如何从标记到未标记的数据中学习公共语义。 将标记数据和未标记数据分开处理往往会阻碍知识从标记数据到未标记数据的转移。

2.3 复制粘贴

复制粘贴是一种简单而强大的数据处理方法，适用于许多任务，如实例分割[7,9]、语义分割[6,25]和对象检测[5]。 一般来说，复制粘贴是指复制一个图像的作物，并粘贴到另一个图像上。 MIXUP[43]和CutMIX[42]分别是混合整体图像和混合图像作物的经典之作。 许多最近的工作扩展了它们以解决特定的目标。 GuidedMix-Net[25]利用MixUp将已标记数据的知识转移到未标记数据中，从而生成高质量的伪标记。 Instaboost[7]和Contextual Copy-Past[5]根据周围的视觉环境，将裁剪后的前景精心地放置到另一幅图像上。 CP2[27]提出了一种预训练方法，将随机裁剪从一幅图像复制粘贴到另一幅背景图像中，该方法被证明更适合于下游密集预测任务。 [9]对实例分割中的复制粘贴进行了系统的研究。 UCC[6]在训练过程中复制属于置信度得分较低的类的像素作为前景，以缓解分布不匹配和类不平衡的问题。 以往的方法只考虑交叉复制粘贴未标记的数据，或者简单地从标记数据中复制作物作为前景，粘贴到另一个数据中。 他们忽略了为标记和未标记数据设计一致的学习策略。 因此，很大的分配差距仍然是不可避免的。

3. 方法

在数学上，我们将医学图像的三维体积定义为$\text{X}\in {\mathbb{R}}^{W\times H\times L}$。

半监督医学图像分割的目标是预测每体素标签图 Y ^ ∈ { 0 , 1 , . . . , K − 1 } W × H × L \widehat{\mathbf{Y}}\in\{0,1,...,K-1\}^{W\times H\times L} Y ∈{0,1,...,K−1}W×H×L，表示背景和目标在$X$中的位置。$K$是类的编号。

我们的训练集$D$由$N$个标记的数据和$M$个未标记的数据组成$N\ll M$，表示为两个子集： $\mathcal{D}={\mathcal{D}}^l\cup {\mathcal{D}}^u$，其中${\mathcal{D}}^l=\{({\mathbf{X}}_i^l,{\mathbf{Y}}_i^l){\}}_{i=1}^N$， D u = { X i u } i = N + 1 M + N . \mathcal{D}^u=\{\mathbf{X}_i^u\}_{i=N+1}^{M+N}. Du={Xiu​}i=N+1M+N​.。

所提出的双向复制粘贴方法的整体流水线如图3所示，在平均教师架构中。我们从训练集中随机挑选两幅无标签的图像$({\mathbf{X}}_p^u,{\mathbf{X}}_q^u)$和两幅有标签的图像$({\mathbf{X}}_i^l,{\mathbf{X}}_j^l)$。

然后我们从${\mathbf{X}}_i^l$（前景）复制粘贴一个随机裁剪到${\mathbf{X}}_q^u$（背景）上，生成混合图像${\mathbf{X}}^{out}$，从${\mathbf{X}}_p^u$（前景）复制粘贴到${\mathbf{X}}_j^l$（背景），生成另一个混合图像${\mathbf{X}}^{in}$。

未标记的图像能够从标记的图像中学习全面的共同语义，从内向（${\mathbf{X}}^{in}$）和外向（${\mathbf{X}}^{out}$）两个方向。然后，图像${\mathbf{X}}^{in}$和${\mathbf{X}}^{out}$被送入学生网络，以预测分割掩码${\hat{\mathbf{Y}}}^{in}$和${\hat{\mathbf{Y}}}^{out}$ 。通过双向复制教师网络中未标记图像的预测结果和已标记图像的标签图，对分割遮罩进行监督。

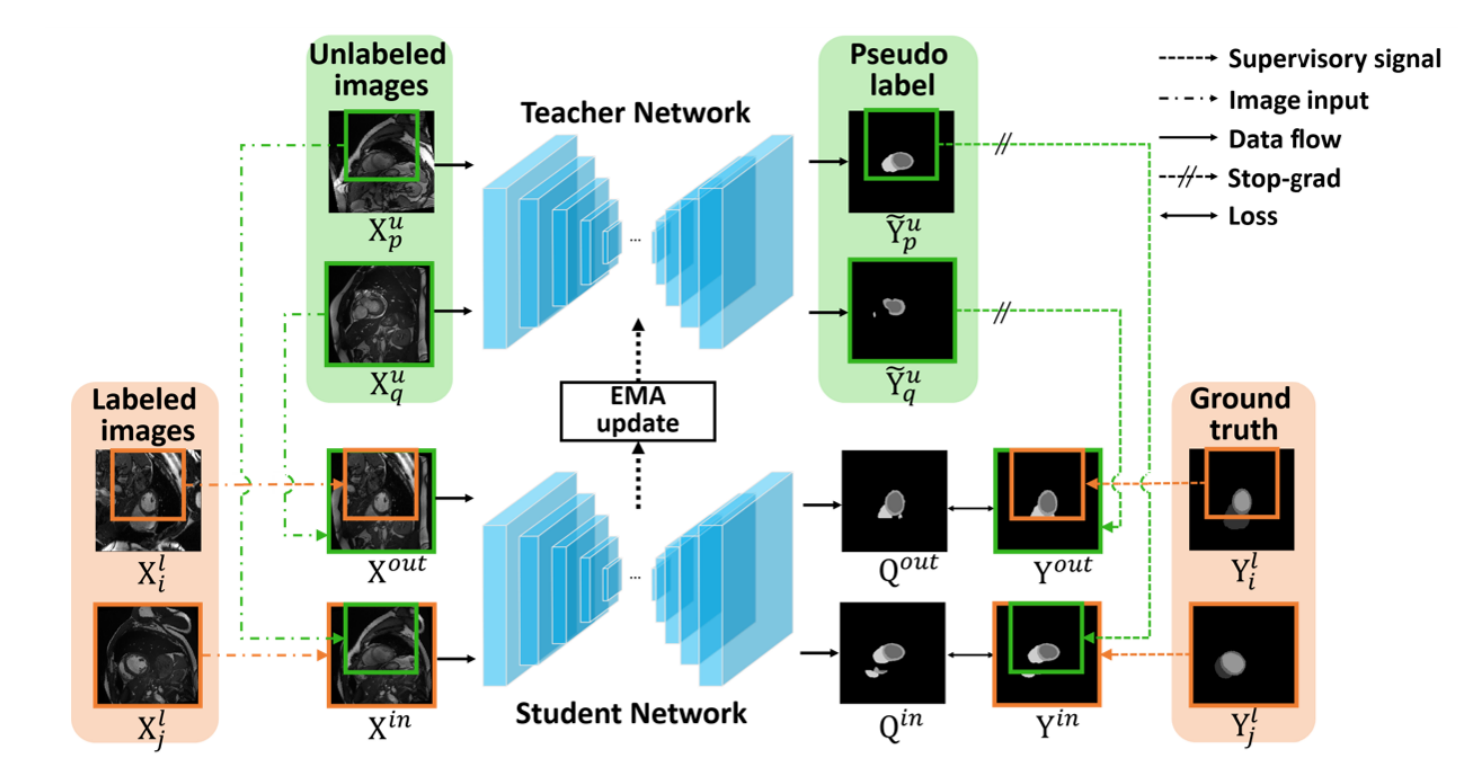
我们的双向复制粘贴框架在Meaner架构中的概述，为了更好的可视化，用2D输入绘制。学生网络的输入是通过将两张有标签的图像和两张无标签的图像以拟议的双向复制粘贴方式混合生成的。然后，为了给学生网络提供监督信号，我们通过同样的双向复制粘贴，将教师网络产生的地面真相和伪标签合并成一个监督信号，以实现地面真相的强监督帮助伪标签的弱监督。

3.1 双向复制粘贴

3.1.1 平均教师和训练策略

在我们的BCP框架中，有一个教师网络，${\mathcal{F}}_t\left({\mathbf{X}}_p^u,{\mathbf{X}}_q^u;{\mathbf{\Theta }}_t\right)$，和一个学生网络${\mathcal{F}}_s\left({\mathbf{X}}^{in},{\mathbf{X}}^{out};{\mathbf{\Theta }}_s\right)$，其中${\Theta }_t$和${\Theta }_s$是参数。学生网络通过随机梯度下降法进行优化，教师网络是通过学生网络的指数移动平均法（EMA）。

我们的训练策略分为三个步骤。

首先，我们只使用标记的数据来预训练模型，然后我们使用预训练的模型作为教师网络来为未标记的图像生成伪标签。在每个迭代中，我们首先通过随机梯度下降优化学生网络参数${\Theta }_s$。最后，我们使用学生参数${\Theta }_s$的EMA更新教师网络参数${\Theta }_t$。

3.1.2 通过复制粘贴进行预训练

受前人[9]的启发，我们对有标签的数据进行复制粘贴增强，训练一个监督模型，监督模型在自训练过程中会对无标签的数据生成伪标签。 该策略被证明有效地提高了分割性能，更多细节将在烧蚀研究中得到说明。

3.1.3 双向复制粘贴图像

为了在一对图像之间进行复制粘贴，我们首先生成一个零中心掩码 M ∈ { 0 , 1 } W × H × L {\mathcal{M}}\in\{0,1\}^{W\times H\times L} M∈{0,1}W×H×L，指示体素来自前景（0）还是背景（1）图像。 零值区域的大小为$\beta H\times \beta W\times \beta L$，其中$\beta \in (0,1)$。 然后我们双向复制粘贴标记和未标记的图像，如下所示：
$$\begin{array}{c}{\mathbf{X}}^{in}={\mathbf{X}}_j^l\odot \mathcal{M}+{\mathbf{X}}_p^u\odot \left(1-\mathcal{M}\right),\\ {\mathbf{X}}^{out}={\mathbf{X}}_q^u\odot \mathcal{M}+{\mathbf{X}}_i^l\odot \left(1-\mathcal{M}\right),\end{array}$$
其中 X i l , X j l ∈ D l , i ≠ j , X p u , X q u ∈ D u , p ≠ A q , 1 ∈ { 1 } W × H ~ × L \mathbf{X}_{i}^{l},\mathbf{X}_{j}^{l}\in\mathcal{D}^{l},i\neq j,\mathbf{X}_{p}^{u},\mathbf{X}_{q}^{u}\in\mathcal{D}^{u},p\neq Aq,\textbf{1}\in\{1\}^{W\times\tilde{H}\times L} Xil​,Xjl​∈Dl,i=j,Xpu​,Xqu​∈Du,p=Aq,1∈{1}W×H~×L, $\odot$指元素明智的乘法。为了保持输入的多样性，采用了两张有标签和无标签的图像。

3.1.4 双向复制粘贴监控信号

为了训练学生网络，还通过BCP操作生成监控信号。 将未标记的图像${\mathbf{X}}_p^u$和${\mathbf{X}}_q^u$输入教师网络，计算它们的概率图：
$${\mathbf{P}}_p^u={\mathcal{F}}_t({\mathbf{X}}_p^u;{\mathbf{\Theta }}_t),{\mathbf{P}}_q^u={\mathcal{F}}_t({\mathbf{X}}_q^u;{\mathbf{\Theta }}_t).$$
初始伪标记${\hat{\mathbf{Y}}}^u$（为了简单起见，去掉p和q）是通过对二值分割任务在${\mathbf{P}}^u$上取公共阈值0.5来确定的，或者对多类分割任务在${\mathbf{P}}^u$上取Argmax运算来确定的。 通过选取${\tilde{\mathbf{Y}}}^u$的最大连通分量，得到最终的伪标记${\tilde{\mathbf{Y}}}^u$，有效地去除离群体素。 然后，我们提出采用与公式1和公式2相同的方式双向复制粘贴未标记图像的伪标签和标记图像的地面真值标签，以获得监督信号：
$$\begin{array}{c}{\mathbf{Y}}^{in}={\mathbf{Y}}_j^l\odot \mathcal{M}+{\tilde{\mathbf{Y}}}_p^u\odot \left(1-\mathcal{M}\right),\\ {\mathbf{Y}}^{out}={\tilde{\mathbf{Y}}}_q^u\odot \mathcal{M}+{\mathbf{Y}}_i^l\odot \left(1-\mathcal{M}\right).\end{array}$$
${\mathbf{Y}}^{in}$和${\mathbf{Y}}^{out}$将作为监督，监督${\mathbf{X}}^{in}$和${\mathbf{X}}^{out}$的学生网络预测。

3.2 损失函数

学生网络的每张输入图像都由标记过的和未标记过的图像的成分组成。直观地说，已标注图像的地面真实掩码通常比未标注图像的伪标签更准确。我们用α来控制未标记图像像素对损失函数的贡献。${\mathbf{X}}^{in}$和${\mathbf{X}}^{out}$的损失函数的计算方法分别为
$$\begin{array}{rl}& {\mathcal{L}}^{in}={\mathcal{L}}_{seg}\left({\mathbf{Q}}^{in},{\mathbf{Y}}^{in}\right)\odot \mathcal{M}+\alpha {\mathcal{L}}_{seg}\left({\mathbf{Q}}^{in},{\mathbf{Y}}^{in}\right)\odot \left(1-\mathcal{M}\right)\\ & {\mathcal{L}}^{out}={\mathcal{L}}_{seg}\left({\mathbf{Q}}^{out},{\mathbf{Y}}^{out}\right)\odot (1-\mathcal{M})+\alpha {\mathcal{L}}_{seg}\left({\mathbf{Q}}^{out},{\mathbf{Y}}^{out}\right)\odot \mathcal{M},\end{array}$$
其中${\mathcal{L}}_{seg}$是Dice损失和交叉熵损失的线性组合。 ${\mathbf{Q}}^{in}$和${\mathbf{Q}}^{out}$的计算方法是：
$${\mathbf{Q}}^{in}={\mathcal{F}}_s({\mathbf{X}}^{in};{\Theta }_s),{\mathbf{Q}}^{out}={\mathcal{F}}_s({\mathbf{X}}^{out};{\mathbf{\Theta }}_s).$$
在每一次迭代中，我们用损失函数通过随机梯度下降更新学生网络中的参数${\Theta }_s$：
$${\mathcal{L}}_{all}={\mathcal{L}}^{in}+{\mathcal{L}}^{out}.$$

4. 实验