队列基础

queue 是以顺序的方式维护的一组数据集合
相对于链表来说，队列操作数据的位置是固定的只能2端操作。
在一端添加数据，从另一端移除数据。习惯来说，添加的一端称为尾，移除的一端称为头，就如同生活中的排队买商品、等等排队的情况。
先进先出

队列的实现

队列的实现方式有很多种

链表实现

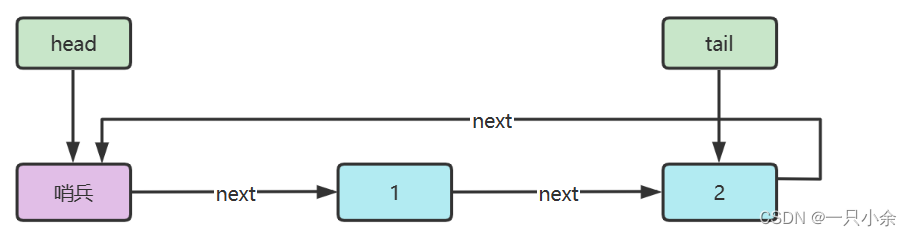
在java中linkedlist可以直接当作队列来使用

LinkedList实现了Deque接口也就是双端队列接口。

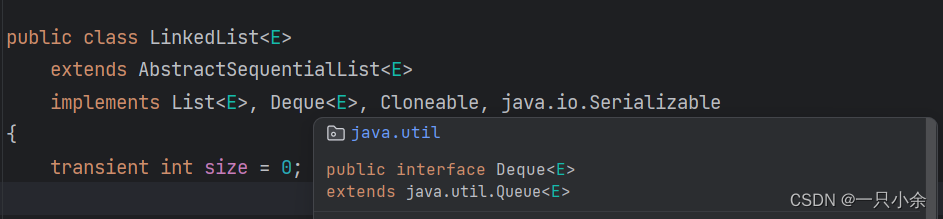
那么链表如何实现队列呢。

维护一个头尾指针

然后其他的就是linked插入和删除了。没啥好讲的了。

环形数组实现

如果是普通数组实现，添加比较快，但是删除，则需要后面元素全部向前移动会非常的慢。
但是环形数组就没有这样的问题了。

java实现类
ArrayBlockingQueue 有界阻塞队列
此类支持一个可选的公平策略，用于对等待的生产者和消费者线程进行排序
ArrayDeque可调整大小的数组实现
所有这些操作都在线性时间内运行。

环形数组，起点和终点是自由的。

下标计算
如数组长度4，起点3，第二个元素的下标为$(3+2)\%4=1$

为空判断
头指针等于尾指针

为满判断

1. (尾指针+1)%len=头指针
2. 尾指针-头指针=len，这个时候头尾指针+1的时候不在取模，一直向上加
3. 计数元素个数

tail一直加的问题

tail一直向上加会有超出int/10范围的可能，会导致计算错误。
如:tail超出$2^{31}-1$就会导致计算时tail为负数。取模运算错误。找不到索引
而且这样取模的运算性能也不高。

解决方案：

• 容量设置为 $2^n$
• 计算取模的时候用按位与一个 $2^n-1$

如:计算最后的一个元素的索引

index = tail & capacity - 1

原理:
取模就是把多余的去掉。
如果按位与—那么如：
一个数与00001111按位取与
那么高的位数全部会为0，保留最后4位。

容量处理

所以我们在设置容量的时候需要讲容量转换为 $2^n$
首先需要检查是否为 $2^n$
检测：

//返回是否满足 2^n
return (capacity & capacity - 1) == 0 

如果不满足我们可以抛出异常或者将起转换为距离比他大的其最小的 $2^n$

1. log处理

n = Math.log10(n-1)/Math.log10(2) + 1

2. 位运算
   我们知道找到这样一个数就是可以将其后面数字全部为1后加1.
   假设要求数c有n位二进制数
   让这个数减一后 c -= 1
   或一个数右移一位 c |= c >>1

这样从左到右第二位数就一定是1了
这样我们就有第一二位都为1了

或一个c右移2为 c|= c>>2

这样1-4位都为1了

依次类推
最后到>>16位就可以将int全部满足了
最后+1就可以了

队列的使用

BFS广度遍历