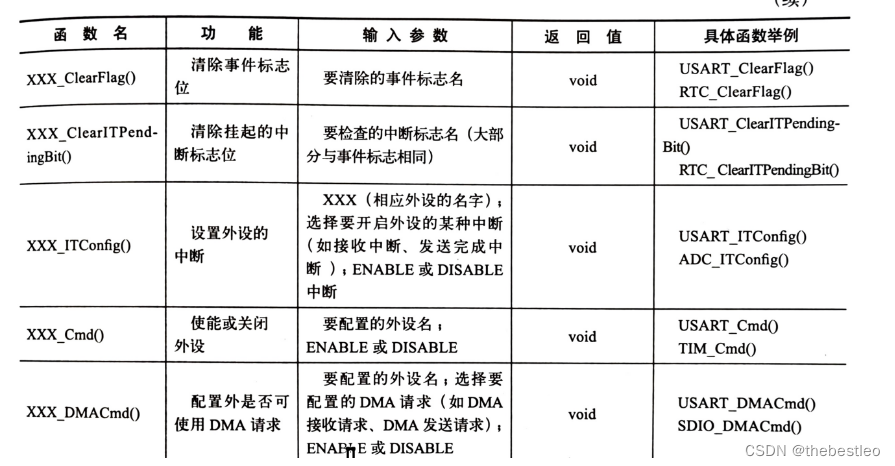
240. 搜索二维矩阵 II（中等）

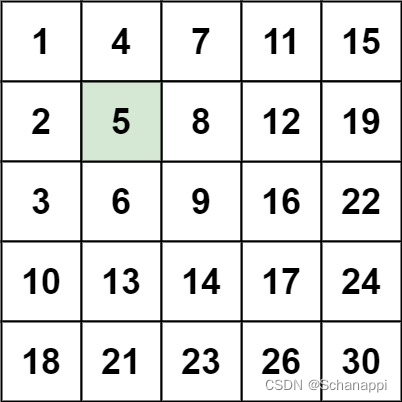
这道题和 74. 搜索二维矩阵 基本一致，可以放在一起做。

方法一：变形的二叉搜索树

思路

• 这种做法和 74. 搜索二维矩阵完全一致。

• 我们可以将二维矩阵抽象成「以右上角为根的 BST」：
  

• 那么我们可以从根（右上角）开始搜索，如果当前的节点不等于目标值，可以按照树的搜索顺序进行：

  • 当前节点「大于」目标值，搜索当前节点的「左子树」，也就是当前矩阵位置的「左方格子」，即 y–；
  • 当前节点「小于」目标值，搜索当前节点的「右子树」，也就是当前矩阵位置的「下方格子」，即 x++。

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        // 当前查找的位置，从右上角开始查找
        int x=0, y = n-1;

        while(check(x, y, m, n) && matrix[x][y] != target){
            if(matrix[x][y] > target)   y--;
            else x++;
        }
        return check(x, y, m, n) && matrix[x][y] == target;
    }
    // 边界情况判断
    bool check(int x, int y, int m, int n){
        return x>=0 && x<m && y>=0 && y<n;
    }
};

方法二：逐行（列）二分

思路

• 由于这道题没有保证后一行的元素一定比前一行都大，因此不能使用二次查找。只能够对数组的每一行进行二分查找。
• 这里也可以使用基本模板，因此每一行的二分查找只有找得到和找不到两种情况。

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        // 逐行进行二分查找
        for(int i=0; i<m; ++i){
            int left = 0, right = n-1;
            while(left <= right){
                int mid = left + (right - left) / 2;
                if(matrix[i][mid] == target) return true;   
                else if(matrix[i][mid] < target) left = mid + 1;
                else right = mid - 1;
            }
        }
        return false;
    }
};