写在前面

由于代码较多，本文仅展示部分关键代码，需要代码文件和数据可以留言

然而，由于当时注释不及时，且时间久远，有些细节笔者也记不清了，代码仅供参考

0 引言

岩爆是深部岩土工程施工过程中常见的一种地质灾害，它是处于高应力或极限平衡状态的岩体或地质结构体在开挖活动的扰动下，其内部储存的应变能瞬间释放，造成开挖空间周围部分岩石从母岩体中急剧、猛烈地突出或弹射出来的一种动态力学现象。由于高应力状态的硬、脆性围岩快速释放蓄积的弹性能，岩爆通常表现为碎片剥落、岩块动力弹射抛掷现象，并伴有不同程度的爆炸、撕裂声。岩爆本身具有突发性、随机性与危险性极大等特点，不仅影响工程进度，更是给地下工程作业人员带来巨大安全隐患，造成不必要的经济损失。因此，随着矿山开采和地下工程规模的不断扩大，岩爆问题日益突出，探明岩爆类型预测方法显得尤为重要。

岩爆类型预测是防治和控制岩爆灾害提前发生最有效的方式之一。岩爆类型预测主要分为单因素预测方法与多因素综合预测方法。单因素预测方法主要是在岩爆发生机制的基础上建立起来的岩爆判据，如Russenes判据和Turchaninov判据、Hoek判据和N-Jhelum判据等。这类理论判据的提出大多基于特定的工程背景，而岩爆诱发机制错综复杂，因此单因素预测方法的准确度通常较低，泛化能力较弱。近年来，为提高岩爆类型预测准确率与可靠性，多因素综合预测方法得到了较快的发展，该方法主要是利用非线性理论综合多种岩爆判据与岩石力学参数实现岩爆预测，主要有数学方法与智能算法两类。数学方法主要有模糊数学综合评判法、逼近理想解排序法、灰色系统理论、云模型理论等。数学方法通常需要人为确定指标权重，受人为主观影响明显，无法客观预测岩爆类型。智能算法主要包括机器学习与深度学习算法等，其中数据量的大小直接影响深度学习的性能，而目前已知的岩爆训练数据量仍旧较少，且神经网络模型存在“黑箱子”现象，无法有效理解内部机制。

机器学习算法具有逻辑简单、模型泛化能力强、训练速度快和适用于小样本等优点，引起国内外学者的兴趣。李明亮等采用6种机器学习算法结合交叉验证建立岩爆预测模型，但未将训练集与测试集分开进行标准化处理，且岩爆工程案例仅有145组，可靠性较差。汤志立等对原始数据集进行过采样与主成分分析等预处理后建立9个考虑多因素的岩爆预测模型，预测结果好于传统理论判据预测结果。吴顺川等基于岩爆案例数据建立PCA-PNN岩爆类型预测模型，模型收敛速度快，预测结果合理。田睿等以独立四因素为训练样本，基于深度学习技术构建DA-DNN模型，模型避开指标权重的确定问题，使模型能够从客观的角度预测岩爆类型。J.Zhou等采用10种有监督学习算法进行岩爆类型预测，并采用准确率与Kappa等指标对比不同算法的预测性能。在已有研究中，大多数研究是在少于200组岩爆案例数据的基础上建立的预测模型，样本量较小，模型的可靠性与泛化能力较差。同时，在对训练集与测试集上进行标准化、过采样、主成分分析等数据预处理时较不规范，如主成分分析预处理时并非首先对训练集进行主成分分析得到转换矩阵后再对测试集进行转换、划分数据集时未按类别比例划分训练集与测试集、对原始数据集进行过采样后再划分训练集与测试集等，这些都会导致训练集信息泄露从而对测试集造成影响，最终影响模型预测结果可靠性。

为了提高模型预测的可靠性与准确率，本文通过文献检索建立了包含397组岩爆工程案例，并选用最近邻、支持向量机、决策这3种在岩爆类型分类性能上表现较好的机器学习算法作为预测模型进行训练，通过规范数据集划分、数据预处理与模型验证等操作，避免训练集信息泄露对测试集造成影响，旨在提高模型预测的可靠性。首先，分析主成分分析法（PCA）对3种机器学习模型的适用性，并通过可视化降维后的数据集解释主成分分析失效原因；其次，为降低原始数据集的不平衡性，采用SMOTE过采样进行预处理，并与原始数据集预测效果进行对比；最后，分析3种机器学习模型低估或者高估岩爆类型的情况，并采用准确率、精确率、召回率、F1值、宏平均与微平均等指标对3个机器模型的分类性能进行评估，从而选出最适合岩爆类型预测的机器学习模型。

1 数据与方法

1.1 指标分析与数据来源（需要数据留言）

（1）指标分析

岩爆发生机制错综复杂，而岩爆评价指标众多，指标选取过多会造成某些指标实测值不易获取而增加预测过程的复杂性，指标选取太少又不能反映预测过程的全面性，导致结果与实际不符。因此，岩爆评价指标的选取是预测的关键。

在工程实例中，首先，岩爆通常发生在应力集中程度较高或者构造应力较高的岩体中，因此可以采用围岩最大切向应力（MTS）作为指标来反应这一现象；其次，岩爆断面形式主要是张拉破坏，因此选取岩石的单轴抗拉强度（UTS）作为岩爆预测指标；再次，岩爆主要发生在结构完整的硬岩中，而岩石的单轴抗压强度（UCS）通常用来衡量岩石的坚硬程度，因此选取该指标作为岩爆预测指标；最后，由于高能储体的应力接近岩体强度是岩爆产生的内因，因此选取岩石弹性能量指数（Wet）作为岩爆预测指标。汤志立等还考虑了深度，但该指标缺失占比达24.31%，采用空值填充算法可靠性较差，而且深度与单轴抗压强度等指标具有一定的相关性，故深度指标的引入无法为数据集提供更多信息。

为了能够从不同角度反应岩爆特征信息，在选取MTS、UTS与UCS等指标的基础上，根据传统岩爆判据构建组合式的岩爆评价指标，同时选取最大切向应力与单轴抗压强度之比（SCF）、脆性系数（单轴抗压强度与单轴抗拉强度之比B1）、岩体应力系数（单轴抗压与单轴抗拉强度之差与单轴抗压与单轴抗拉强度之和的比值B2）。因此，本研究总共选取7个指标作为岩爆类型预测指标。

岩爆预测结果以岩爆类型直观表示，在现有的岩爆预测评价体系中，通常以岩爆发生的剧烈程度及破坏特征，将岩爆划分为4类：无岩爆（None, N）、轻微岩爆（Light, L）、中等岩爆（Moderate, M）与强岩爆（Strong, S）。

（2）数据来源

为了衡量各种机器学习算法的性能与适用性，本文使用的397组岩爆案例均来自于已发表文章，其中331组来自Zhou and Li等、46组来自Dong and Li、20组来自周科平等，本文对部分与原始数据不符的数据进行修正。

将已知类别的原始岩爆数据集的各类别分别按8：2的比例随机分为训练集与测试集两个子集，避免测试集与训练集样本分布不一致。采用shuffle函数对数据集进行随机打乱处理，且为了保证模型的复现性，分割时将shuffle函数的随机数种子设置为1，从而使每次分割的结果相同，保证结果可比性。

①训练集：用于估计模型参数并构建各岩爆分类器模型；本研究考虑397个数据集中的317个（约现有数据的80%）；

②测试集：作为独立验证集，测试各模型的性能和预测能力；本研究保留80个（约现有数据的20%）数据集作为测试数据集。

代码：训练集与测试集按类别比重划分

#按类别8:2划分数据集
rd = 1
ratio = 0.8

train_data_1,test_data_1 = train_test_split(shuffle(data[data["y"]==1],random_state=rd),test_size=0.2,random_state=rd,shuffle=True)
train_data_2,test_data_2 = train_test_split(shuffle(data[data["y"]==2],random_state=rd),test_size=0.2,random_state=rd,shuffle=True)
train_data_3,test_data_3 = train_test_split(shuffle(data[data["y"]==3],random_state=rd),test_size=0.2,random_state=rd,shuffle=True)
train_data_4,test_data_4 = train_test_split(shuffle(data[data["y"]==4],random_state=rd),test_size=0.2,random_state=rd,shuffle=True)

train_data = train_data_1.append(train_data_2).append(train_data_3).append(train_data_4)
test_data = test_data_1.append(test_data_2).append(test_data_3).append(test_data_4)

data_temp = train_data.copy()
data_temp_test = test_data.copy()

train_data_temp = (train_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]-train_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].mean())/train_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].std()

1.2 数据描述与数据预处理

（1）数据描述

对于岩爆评价指标，397组岩爆案例的7个评价指标统计参数见表1。从该表可以看出，随着指标MTS、UCS、UTS与Wet均值的增加，岩爆类型总体逐渐从N变化到S，但四个指标标准差较大，且SCF、B1与B2三个指标与岩爆类型并无明显规律，这都增加了岩爆类型预测的难度，使得无法直接根据单一指标判定岩爆类型。

表1 不同类型岩爆预测指标统计参数

岩爆类型	统计参数	MTS	UCS	UTS	SCF	B1	B2	Wet
N	mean	25.11	95.58	5.58	0.41	20.74	0.87	2.84
	std	20.01	47.12	3.33	0.83	11.72	0.07	1.93
	min	2.60	18.30	0.40	0.05	5.38	0.69	0.81
	max	107.50	237.10	17.66	5.27	47.97	0.96	7.80
L	mean	48.29	117.29	6.99	0.50	20.80	0.88	3.88
	std	25.43	47.70	4.10	0.54	10.45	0.07	1.75
	min	13.50	26.10	0.80	0.10	2.52	0.43	0.85
	max	148.40	263.00	22.60	4.54	69.69	0.97	9.00
M	mean	55.53	123.65	7.04	0.49	23.78	0.89	5.44
	std	22.70	46.34	4.33	0.26	15.86	0.05	2.47
	min	16.30	30.00	1.30	0.10	5.53	0.69	2.00
	max	132.10	304.00	19.20	2.57	80.00	0.98	21.00
S	mean	113.46	128.61	9.93	1.11	14.97	0.85	8.42
	std	77.65	57.67	5.06	1.08	6.57	0.06	5.58
	min	16.43	30.00	2.50	0.10	5.53	0.69	1.90
	max	297.80	306.58	22.60	4.87	32.24	0.94	30.00

代码：

data = pd.read_csv("read_data_new_duplicate.csv",encoding="gbk",index_col="no")
data.describe().to_csv("自变量基本信息表.csv")

为了研究本文7个预测指标间的相关性，建立岩爆预测指标之间的相关性矩阵如表2所示。从表2可以看出，部分预测指标间具有较强的相关性，这是由于传统岩爆判据基于围岩应力参数进行预测，而SCF、B1与B2是基于围岩应力参数进行组合构建。因此，有必要尝试对7个岩爆预测指标进行PCA预处理，消除指标间的相关性，并将预测结果与原始数据集的预测结果进行对比。

表2 岩爆指标相关性矩阵

	MTS	UCS	UTS	SCF	B1	B2	Wet
MTS	1.00	0.12	0.33	0.77	-0.23	-0.24	0.46
UCS	0.12	1.00	0.54	-0.31	0.04	0.21	0.27
UTS	0.33	0.54	1.00	-0.01	-0.60	-0.63	0.34
SCF	0.77	-0.31	-0.01	1.00	-0.13	-0.19	0.20
B1	-0.23	0.04	-0.60	-0.13	1.00	0.75	-0.11
B2	-0.24	0.21	-0.63	-0.19	0.75	1.00	-0.13
Wet	0.46	0.27	0.34	0.20	-0.11	-0.13	1.00

代码：相关性矩阵

#相关性矩阵
data.corr()

对于岩爆类型，从图1可以看出，岩爆类型为中等岩爆的数量最多，为140例；类型为强岩爆与无岩爆的数量最少，分别为69与73例。这是由于岩爆类型为强岩爆的通常较少，而属于无岩爆的矿山样本由于不存在岩爆而较少搜集相关数据，因此样本存在一定的不均衡性，但最大样本量与最小样本量的比值仅略大于2为2.03。虽然不平衡问题严重性较小，但由于算法通常以最大化总体准确率为目标函数，不平衡问题会导致算法过多关注多数类，降低模型对少数类的分类性能。因此，本文采用SMOTE过采样对训练集进行预处理，消除训练集样本不均衡性，并将预测结果与原始数据集的预测结果进行对比。

图1 岩爆实际等级分布

（2）数据标准化

为保证模型预测的可靠性，KNN与SVM模型需要在输入岩爆预测指标前对数据进行标准化处理，即首先对训练集进行标准化，再利用训练集的均值与标准差，对测试集进行标准化，旨在将数据缩放到相同的区间范围内，消除多个评判指标间量纲的不一致对模型的影响。而对于决策树模型，特征区间的划分与信息熵的变化有关，与各个指标特征大小无关，故该模型无需对数据进行标准化。

数据标准化，应先对测试集进行数据标准化，得到训练集的均值与标准差，再利用训练集的均值与标准差对测试集数据进行标准化，否则会使训练集信息泄露

代码：数据标准化

#数据标准化+label(0-3)
data_norm = (train_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]-train_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].mean())/train_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].std()
data_norm["y"] = train_data["y"]
train_data = data_norm

data_norm = (test_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]-norm_mean)/norm_std
data_norm["y"] = test_data["y"]
test_data = data_norm

（3）主成分分析PCA

从表2可以看出，部分指标之间相关性较强，如单轴抗压强度与单轴抗拉强度相关系数为0.54、最大切向应力与SCF相关系数为0.77、B2与B1相关系数为0.75，故岩爆预测指标之间存在较为明显的相关性。因此，在模型训练前可以尝试采用主成分分析（PCA）对训练集进行特征抽取。

类似数据标准化，应先对测试集进行特征提取，得到预测指标与主成分之间的转换方程，再利用该方程对训练集进行转换，而非将测试集与训练集合并进行预处理

（4）过采样SMOTE

训练集存在类别不平衡现象时，模型将不能充分地从含有少量样本的类别中学习到该类别的特征。SMOTE过采样通过随机采样训练集中少数类生成的合成样本而非实例的副本，从而缓解过拟合问题，并且不会损失有价值的信息。故本文选用SMOTE过采样技术对不平衡数据集进行预处理。

仅对训练集进行SMOTE过采样，无需对测试集进行过采样。通过将训练集新生成的数据与训练集原数据合并，使各类岩爆类型达到平衡。

1.3 机器学习算法

机器学习算法类型较多，其中，线性判别分析（LDA）、二次判别分析（QDA）、偏最小二乘判别分析（PLS-DA）、朴素贝叶斯（NB）、多层感知机（MLP）与AdaBoost等有监督机器学习算法预测准确率低于50%；因此，本文只采用准确率较高的K近邻法（KNN）、支持向量机（SVM）与决策树（DT）模型实现对岩爆类型的预测。

1.4 模型评价方法与指标

（1）n-fold交叉验证

为了提升模型的泛化能力，防止模型过拟合，在训练集上采用多折交叉验证的方法确定模型参数。n-折交叉的方法如下：（a）将训练集通过随机打乱处理平均分为n份；（b）对于这n份样本，依次以其中n-1份为训练集，剩余1份作为验证集，训练模型对验证集进行预测；（c）对n次预测结果做平均处理，作为模型的最终效果。

（2）模型参数优化

模型训练过程中采用网格搜索进行模型参数优化，以获得5折交叉验证下算法平均准确率最高时的最优参数，从而确定KNN算法的最相似标签值的个数k_neighbor、SVM算法的惩罚系数C、决策树算法的最大子树深度max_depth。

（3）性能评价指标

为了评估本文所建立的3种分类模型的泛化性能，借助准确率（Accuracy）、精确率（Precision）、召回率（Recall）与F1值等指标衡量模型泛化能力。对于多分类问题，还涉及宏平均（Macro-averageing）与微平均（Micro-averageing）指标。

2 结果与讨论

2.1 PCA及SMOTE适用性分析

（1）主成分分析PCA对3种机器学习模型的预测准确度对比

基于SK-learn，采用训练集的317组岩爆预测训练集样本进行主成分分析，各主成分方差贡献率及累计贡献率见表3。由于前3个主成分的累计贡献率为85.39%，故将前3个主成分作为机器学习模型的输入。表4为对应主成分系数矩阵。

表3 主成分分析处理结果

成分	特征值	主成分贡献率/%	累计贡献率/%
1	29.61	39.62	39.62
2	23.00	23.91	63.53
3	21.86	21.86	85.39
4	13.61	8.37	93.76
5	9.42	4.02	97.78
6	6.15	1.71	99.49
7	4.12	0.51	100.00

表4 主成分系数矩阵

Index	主成分
Index	RBI1	RBI2	RBI3
MTS	0.42	0.38	-0.34
UCS	0.11	-0.52	-0.52
UTS	0.49	-0.38	-0.02
SCF	0.26	0.65	-0.11
B1	-0.44	0.14	-0.40
B2	-0.45	0.05	-0.45
Wet	0.31	0.01	-0.48

根据主成分系数矩阵（表4），可以得出主成分RBI1、RBI2、RBI3与7个岩爆预测指标之间的关系为：

利用公式（1）~（3）对80组测试集数据进行线性转换，再将降维后的测试集数据作为3种机器学习模型的输入从而实现对岩爆类型预测，有无采用PCA对数据进行预处理后的模型在测试集上的预测准确率如表5所示。从该表可以看出，采用主成分分析预处理略微提高SVM模型的预测准确率，降低了KNN与决策树模型在测试集上的预测准确率。尤其是决策树模型，采用PCA预处理后的准确率降至57.50%，这主要是由于主成分分析首先会对数据进行标准化处理，而决策树算法无需对数据进行标准化处理。因此，主成分分析对于该样本数据提高模型预测准确率并无显著效果。

代码：主成分分析预处理

#主成分分析-数据标准化
modelPCA = PCA(n_components=7)
train_data = modelPCA.fit_transform(train_data_temp[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])
print(modelPCA.singular_values_)  #特征值
print(modelPCA.explained_variance_ratio_)  # 返回 PCA 模型各主成份占比

#主成分分析-数据标准化
modelPCA = PCA(n_components=3)
train_data = modelPCA.fit_transform(train_data_temp[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])


train_data = pd.DataFrame(train_data,index=data_temp.index)
train_data["y"] = data_temp["y"]
train_data.columns = ["RBI1","RBI2","RBI3","y"]
train_data

#主成分分析-主成分系数矩阵
print(modelPCA.components_)

#主成分分析-主成分系数矩阵验证
PCA_components = (np.matrix(train_data_temp[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])).I.dot(train_data[["RBI1","RBI2","RBI3"]])
print(PCA_components)

表5 主成分分析对3机器学习模型预测准确率对比表（%）

	KNN	SVM	DT
无预处理	68.75	57.50	65.00
PCA预处理	66.25	58.75	57.50

代码：PCA预处理后的预测准确率

#1-KNN算法
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score

plt.figure(figsize=(16,8))

x = np.array(train_data[["RBI1","RBI2","RBI3"]])
y = train_data["y"]


knn_x = []
knn_score = []

for eachK in range(1,101):
    knn = KNeighborsClassifier(n_neighbors=eachK)    #实例化KNN模型
    scores = cross_val_score(knn,x,y,cv=5,scoring='accuracy')
    knn_x.append(eachK)
    knn_score.append(np.array(scores).mean())

plt.plot(knn_x,knn_score,marker="o")

test_data = (test_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]-test_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].mean())/test_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].std()
X = test_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].values*PCA_components

count = 0
sum_good = 0

knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(x,y)

for eachX,eachY in zip(knn.predict(X),data_temp_test["y"]):
    if eachX < eachY:
        print(count+1,eachX,eachY)
    if eachX == eachY:
        sum_good += 1
    count += 1

print(sum_good/count)

#2-SVM https://zhuanlan.zhihu.com/p/134091240
#https://blog.csdn.net/MrShuang123/article/details/118308133
from sklearn.svm import SVC
plt.figure(figsize=(16,8))

x = np.array(train_data[["RBI1","RBI2","RBI3"]])
y = train_data["y"]

SVM_x = []
SVM_score = []

for value in [2**i for i in range(-5,10)]:
    test = SVC(kernel="rbf", C=value, decision_function_shape='ovr',gamma="auto") #自动为特征分之1
    scores = cross_val_score(test,x,y,cv=5,scoring='accuracy')
    print(value,np.array(scores).mean())
    SVM_x.append(eachK)
    SVM_score.append(np.array(scores).mean())

plt.plot(list(range(1,16)),SVM_score,marker="o") 

count = 0
sum_good = 0

svm = SVC(kernel="rbf", C=2**8, decision_function_shape='ovr',gamma="auto")
svm.fit(x,y)

for eachX,eachY in zip(svm.predict(X),data_temp_test["y"]):
    if eachX < eachY:
        print(count+1,eachX,eachY)
    if eachX == eachY:
        sum_good += 1
    count += 1

print(sum_good/count)

#3-决策树
plt.figure(figsize=(16,8))

x = np.array(train_data[["RBI1","RBI2","RBI3"]])
y = train_data["y"]

DT_x = []
DT_score = []

for mp in range(5,30):
    
    clf = DecisionTreeClassifier(criterion='entropy',max_depth=mp)
    clf = clf.fit(x,y)
    scores=cross_val_score(clf,x, y,cv=5,scoring='accuracy')#评分方式为accuracy
    print(mp,np.array(scores).mean())
    DT_score.append(scores.mean())

plt.plot(list(range(5,30)),DT_score,marker="o")

count = 0
sum_good = 0

clf = DecisionTreeClassifier(criterion='entropy',max_depth=9)
clf = clf.fit(x,y)

for eachX,eachY in zip(clf.predict(X),data_temp_test["y"]):
    if eachX < eachY:
        print(count+1,eachX,eachY)
    if eachX == eachY:
        sum_good += 1
    count += 1

print(sum_good/count)

原始数据集存在7个岩爆预测指标，采用PCA预处理可以在最大限度保留原始数据集信息的前提下将7维数据通过线性转换投影到二维空间与三维空间，降维后的数据集如图2所示。从图2可以看出，无论是二维还是三维空间，数据集存在较大扰动，岩爆评价指标的微小变动很可能引起岩爆类型的变化，即不同岩爆类型的样本之间不具有较为明显的分类边界，因此PCA无法有效提高岩爆类型预测准确率。

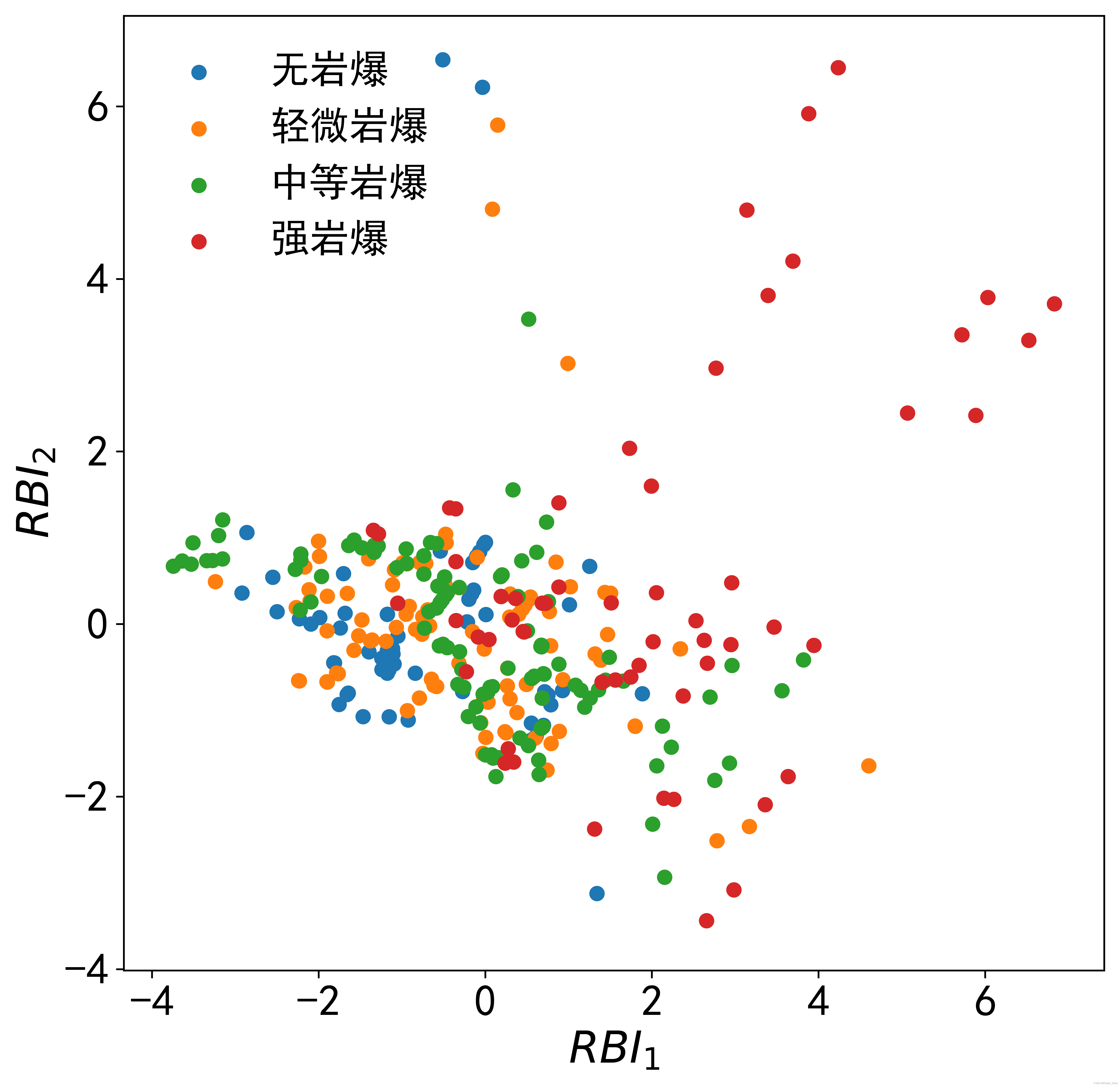图2 降维后样本分布图

代码：2维

#降维-PCA-效果不好
data = pd.read_csv("read_data_new_duplicate.csv",encoding="gbk",index_col="no")
data_norm = (data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]-data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].mean())/data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].std()
data_norm["y"] = data["y"]
data = data_norm

plt.figure(figsize=(8,8))

modelPCA_pic = PCA(n_components=2)
modelPCA_pic.fit(data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])
data_pic = modelPCA_pic.fit_transform(data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])

X_scatter_1 = []
Y_scatter_1 = []
X_scatter_2 = []
Y_scatter_2 = []
X_scatter_3 = []
Y_scatter_3 = []
X_scatter_4 = []
Y_scatter_4 = []

for each,z in zip(data_pic,data["y"]):
#     print(each[0],each[1],z)
    if z == 1:
        X_scatter_1.append(each[0])
        Y_scatter_1.append(each[1])
    if z == 2:
        X_scatter_2.append(each[0])
        Y_scatter_2.append(each[1])
    if z == 3:
        X_scatter_3.append(each[0])
        Y_scatter_3.append(each[1])
    if z == 4:
        X_scatter_4.append(each[0])
        Y_scatter_4.append(each[1])

plt.scatter(X_scatter_1,Y_scatter_1,label="无岩爆")
plt.scatter(X_scatter_2,Y_scatter_2,label="轻微岩爆")
plt.scatter(X_scatter_3,Y_scatter_3,label="中等岩爆")
plt.scatter(X_scatter_4,Y_scatter_4,label="强岩爆")

plt.xlabel("$RBI_1$",fontsize=20)
plt.ylabel("$RBI_2$",fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)


plt.legend(fontsize=18,frameon=False)
plt.savefig("PCA-2维",dpi=1000,bbox_inches = 'tight')

代码：3维

#降维-T-SNE-没有明显决策边界
%matplotlib notebook

data = pd.read_csv("read_data_new_duplicate.csv",encoding="gbk",index_col="no")
data_norm = (data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]-data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].mean())/data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]].std()
data_norm["y"] = data["y"]
data = data_norm

plt.figure(figsize=(8,8))

modelPCA_pic = PCA(n_components=3)
modelPCA_pic.fit(data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])
data_pic = modelPCA_pic.fit_transform(data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]])

X_scatter_1 = []
Y_scatter_1 = []
Z_scatter_1 = []
X_scatter_2 = []
Y_scatter_2 = []
Z_scatter_2 = []
X_scatter_3 = []
Y_scatter_3 = []
Z_scatter_3 = []
X_scatter_4 = []
Y_scatter_4 = []
Z_scatter_4 = []
    

for each,z in zip(data_pic,data["y"]):
#     print(each[0],each[1],z)
    if z == 1:
        X_scatter_1.append(each[0])
        Y_scatter_1.append(each[1])
        Z_scatter_1.append(each[2])
    if z == 2:
        X_scatter_2.append(each[0])
        Y_scatter_2.append(each[1])
        Z_scatter_2.append(each[2])
    if z == 3:
        X_scatter_3.append(each[0])
        Y_scatter_3.append(each[1])
        Z_scatter_3.append(each[2])
    if z == 4:
        X_scatter_4.append(each[0])
        Y_scatter_4.append(each[1])
        Z_scatter_4.append(each[2])

ax = plt.subplot(projection = '3d')
    
plt.xlabel("$RBI_1$",fontsize=20)
plt.ylabel("$RBI_2$",fontsize=20)
ax.set_zlabel("$RBI_3$",fontsize=20)

# plt.xticks(fontsize=18)
# plt.yticks(fontsize=18)
# ax.tick_params(axis="z", labelsize=18)
ax.tick_params(labelsize=18)



ax.scatter(X_scatter_1,Y_scatter_1,Z_scatter_1,label="无岩爆")
ax.scatter(X_scatter_2,Y_scatter_2,Z_scatter_2,label="轻微岩爆")
ax.scatter(X_scatter_3,Y_scatter_3,Z_scatter_3,label="中等岩爆")
ax.scatter(X_scatter_4,Y_scatter_4,Z_scatter_4,label="强岩爆")

plt.legend(fontsize=18,frameon=False)
plt.savefig("PCA-3维",dpi=1000,bbox_inches = 'tight')

（2）过采样SMOTE对3种机器学习模型的预测准确度对比

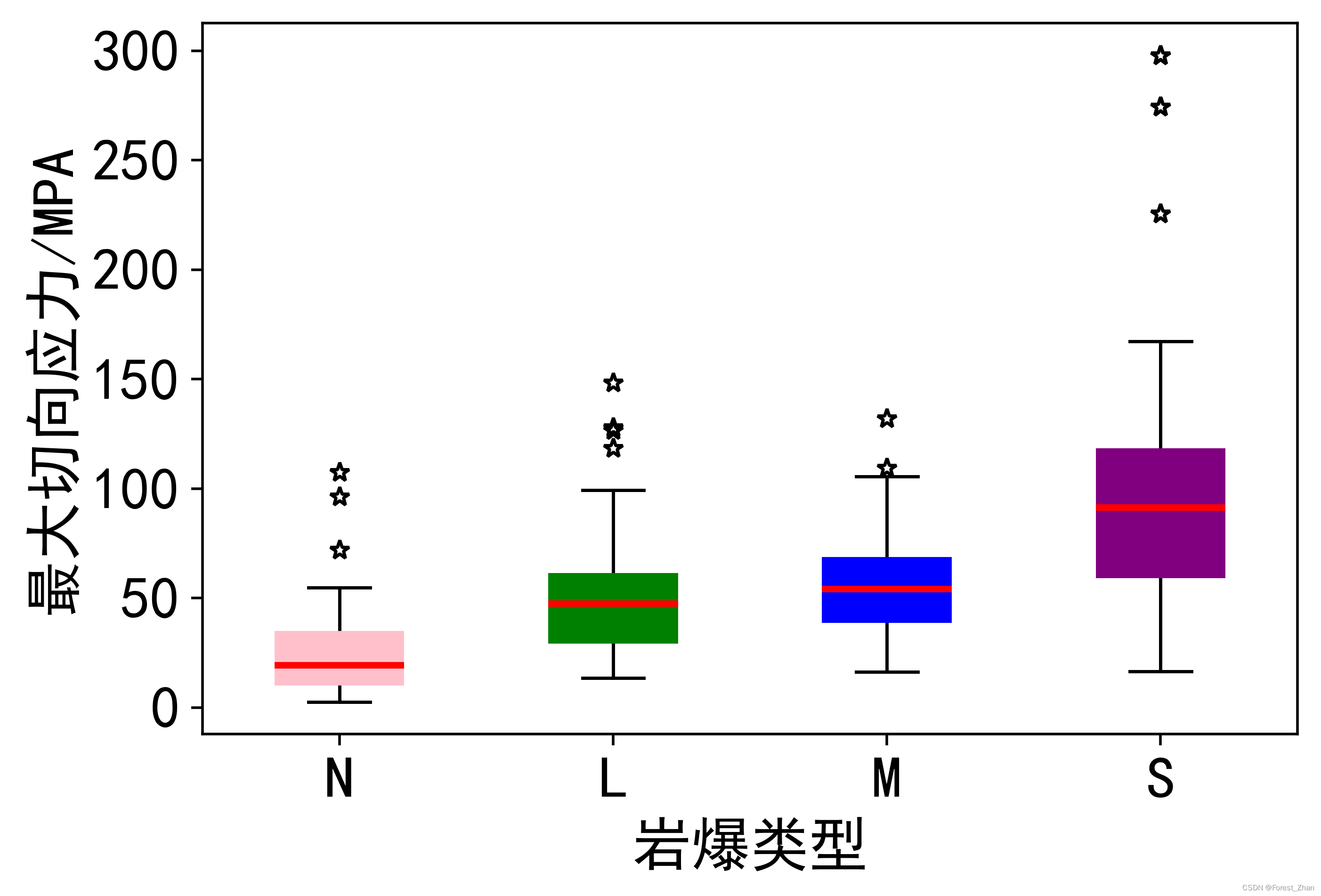
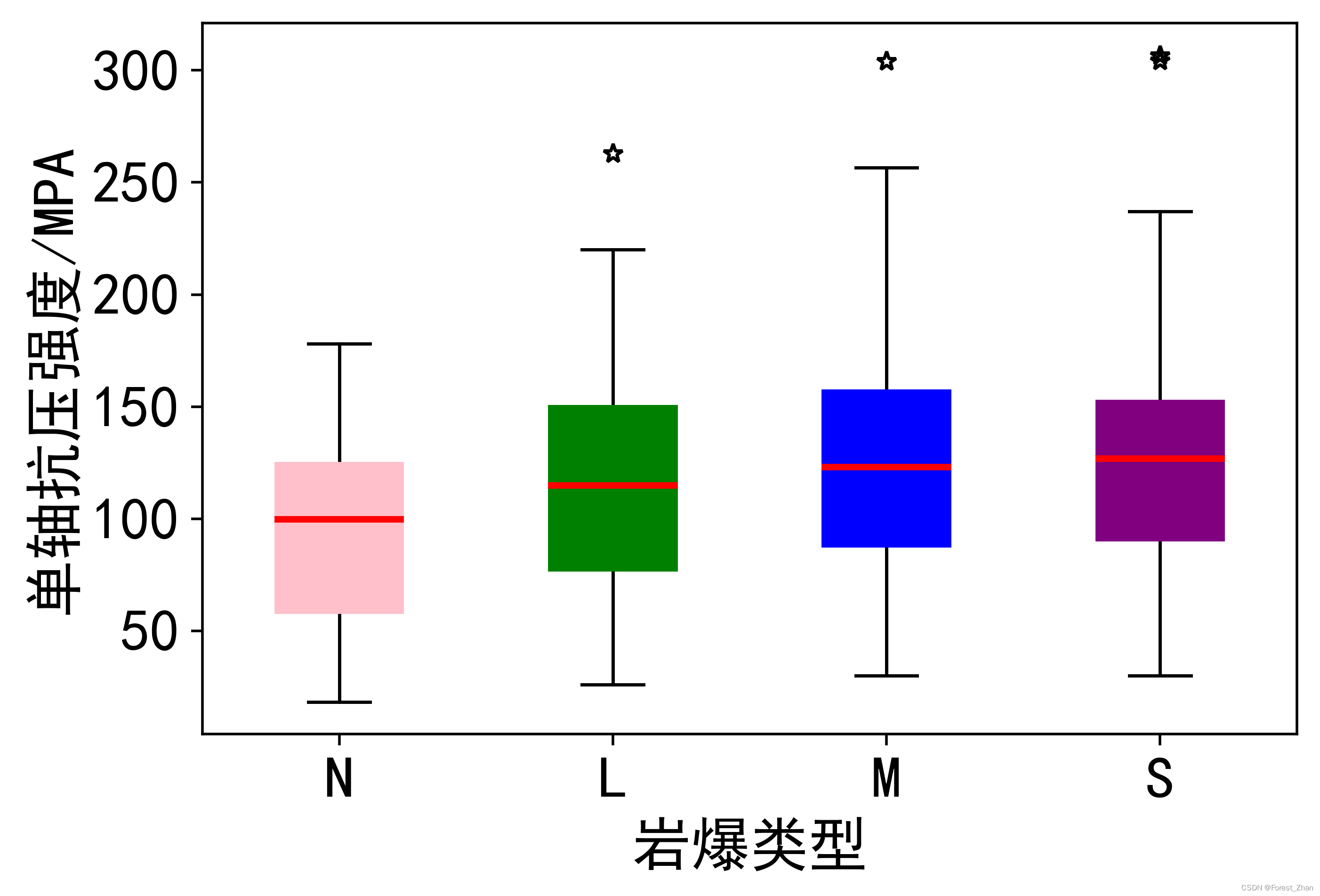
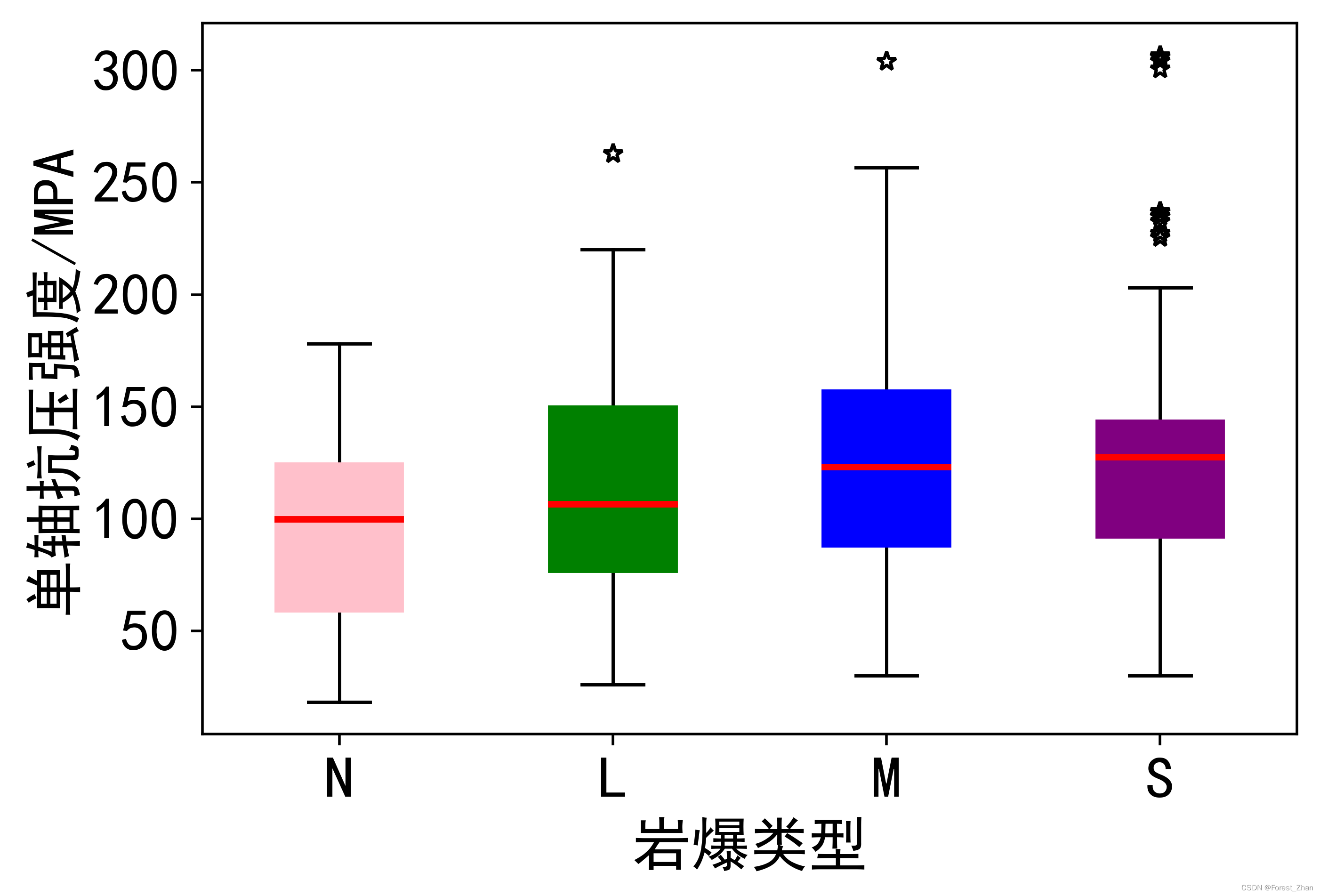
采用SMOTE过采样算法后，样本量由原训练集的317个样本（58个N型严样本，92个L型样本，112个M型样本与55个S型样本）变为448个样本数据（4类岩爆类型均为112个）。从采样前后部分岩爆预测指标箱型图（图3）可以看出，过采样前后数据集整体分布几乎一致，故可以采用过采样后的样本对机器学习模型进行训练。

有无采用SMOTE过采样算法对数据进行预处理后的模型在测试集上的预测准确率如表6所示。从该表可以看出，采用SMOTE过采样算法对原始数据进行预处理后，可以明显提升DT模型算法的准确率，预测准确率从原始数据集的65%提高至过采样预处理后的77.5%。

（a）过采样前-最大切向应力

（b）过采样后-最大切向应力

（c）过采样前-单轴抗压强度

（d）过采样前-单轴抗压强度

图3 过采样前后部分岩爆评价指标箱型图

代码：箱型图

f = plt.boxplot([data_before["sigma_theta"][data_before["y"]==1],
            data_before["sigma_theta"][data_before["y"]==2],
            data_before["sigma_theta"][data_before["y"]==3],
            data_before["sigma_theta"][data_before["y"]==4]],sym='*',labels=["N","L","M","S"],patch_artist=True,
                medianprops={'linewidth': 2,'color': 'red'}
           )


c_list = ['pink', 'green', 'blue',"purple"]  # 颜色代码列表

for box, c in zip(f['boxes'], c_list):  # 对箱线图设置颜色
    box.set(color=c, linewidth=2)
    box.set(facecolor=c)


plt.xlabel("岩爆类型",fontsize=18)
plt.ylabel("最大切向应力/MPA",fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)

plt.savefig("箱型图-sigma_theta-before",dpi=500,bbox_inches = 'tight')

表6 SMOTE对3机器学习模型预测准确率对比表（%）

	KNN	SVM	DT
无预处理	68.75	57.50	65.00
SMOTE预处理	67.50	52.50	77.50

代码：SMOTE预处理代码，其余代码类似PCA，不赘述

#样本不均衡问题-查看具体别类数理->不均衡
#类别1 58
#类别2 92
#类别3 112
#类别4 55
print(len(train_data[train_data["y"]==1]["y"]))
print(len(train_data[train_data["y"]==2]["y"]))
print(len(train_data[train_data["y"]==3]["y"]))
print(len(train_data[train_data["y"]==4]["y"]))

#样本不均衡问题-数据增强
oversample = SMOTE()
x, y = oversample.fit_resample(train_data.iloc[:,:-1], train_data.iloc[:,-1])
x["y"]=y
train_data = x

2.2 三种机器学习模型预测结果分析

（1）模型训练与预测

根据2.1节分析可知，主成分分析PCA与过采样SMOTE预处理对KNN与SVM模型的预测准确率并无提升，而SMOTE算法预处理能够明显提高决策树模型的预测准确率，故本文采用经SMOTE算法预处理的SMOTE-DT模型及仅对原始数据集进行标准化处理的KNN、SVM模型。

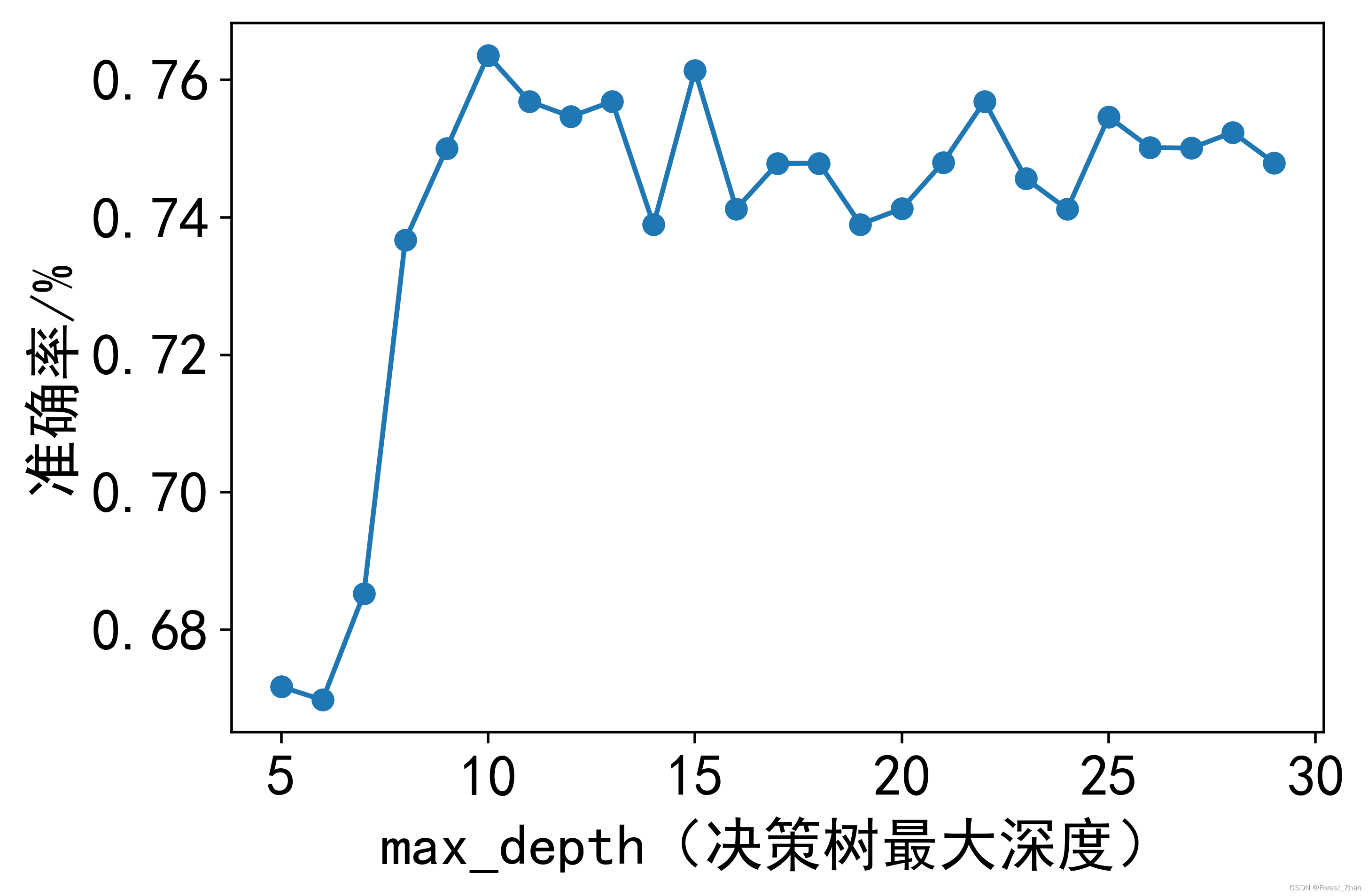
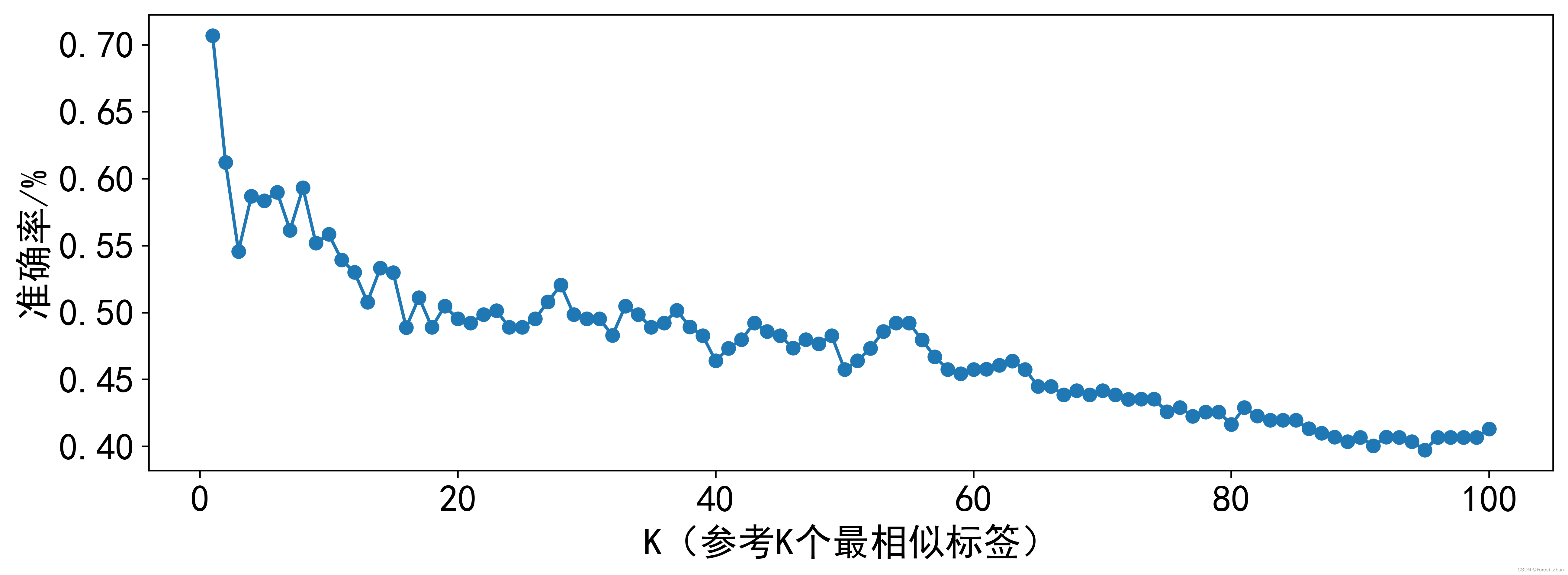
结合5折交叉验证与模型参数优化，可得3种机器学习模型在不同参数下的5折交叉验证结果如图4所示。从图4可以看出，SVM模型中的惩罚系数C的最佳值为256，对应5折交叉验证平均准确率为65.62%；SMOTE-DT模型中决策树最大深度max_depth的最佳值为10，对应5折交叉验证平均准确率为76.36%；KNN模型中的参考最相似标签值的个数k_neighbor最佳参数为1，对应5折交叉验证平均准确率为70.69%。

（a）SVM

（b）SMOTE-DT

（c）KNN

图4 3种机器模型五折交叉验证结果

（2）模型预测结果准确率分析

利用已经训练好的模型对测试集进行测试，KNN、SVM、SMOTE-DT模型预测准确率分别为68.75%、57.50%与77.50%，远高于四分类问题随机分类时的25%，说明3种算法均能通过原始数据集进行有效训练。为了更加直观看出3种机器模型对4类岩爆类型预测情况，将N、L、M与S类型编号为1、2、3、4，采用（预测类型-真实类型）作为纵坐标，测试集样本序号作为横坐标，绘制3种机器模型的预测结果。

KNN、SVM与SMOTE-DT模型预测结果分别如图5~7。可以看出，3种机器学习模型对于4类岩爆类型的预测准确率总体上一致，对测试集样本的高估与低估只会相差1至2级，仅有决策树模型存在高估3个级别。3种模型高估岩爆类型的次数分别为13、14与7次，低估岩爆类型的次数分别为12、20、11次。对于岩爆类型的预测而言，高估岩爆类型虽然会对造成一定的资源浪费，但生产安全性可以得到较好的保障，而低估岩爆类型不仅会影响施工进度，而且不利于人员与设备的安全，容易造成更大的经济损失。SMOTE-DT与KNN模型低估岩爆类型的次数明显低于SVM模型，模型预测更加安全保守，且SMOTE-DT出现高估岩爆类型的情况较其他两种模型也较少，预测准确性与安全保障性均优于KNN与SVM模型。

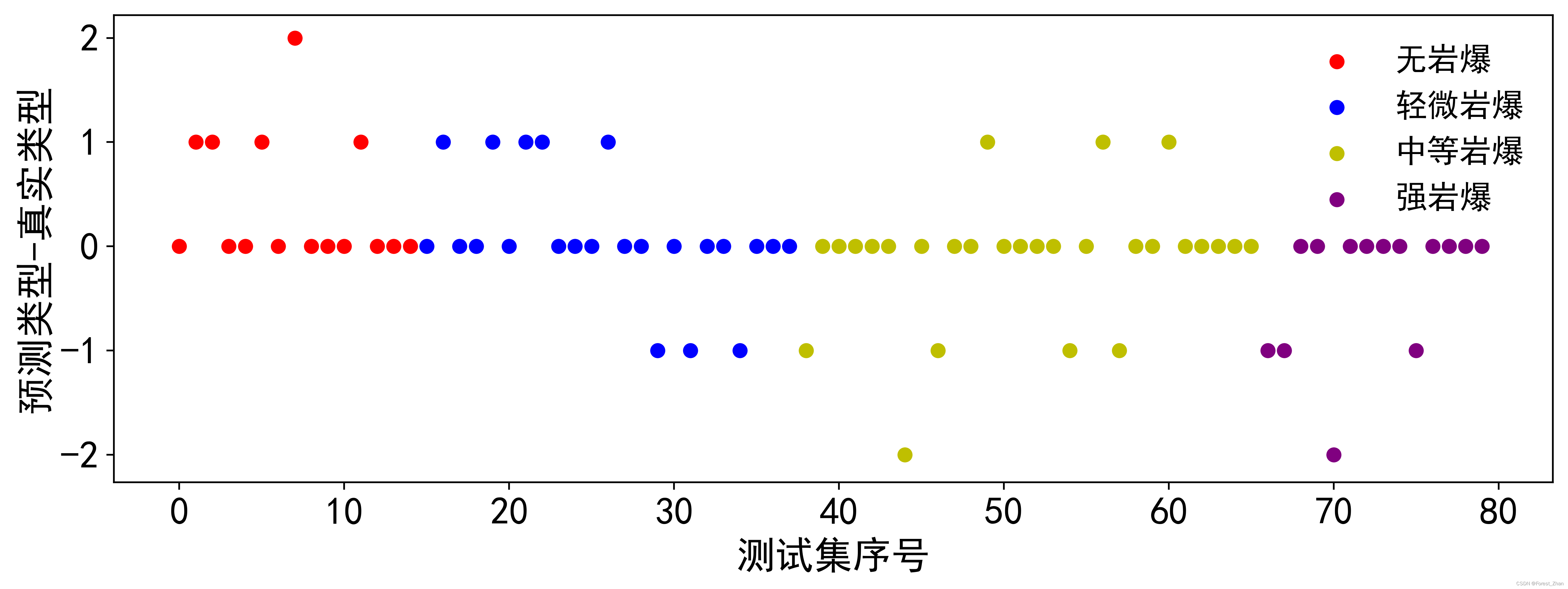
图5 KNN预测结果

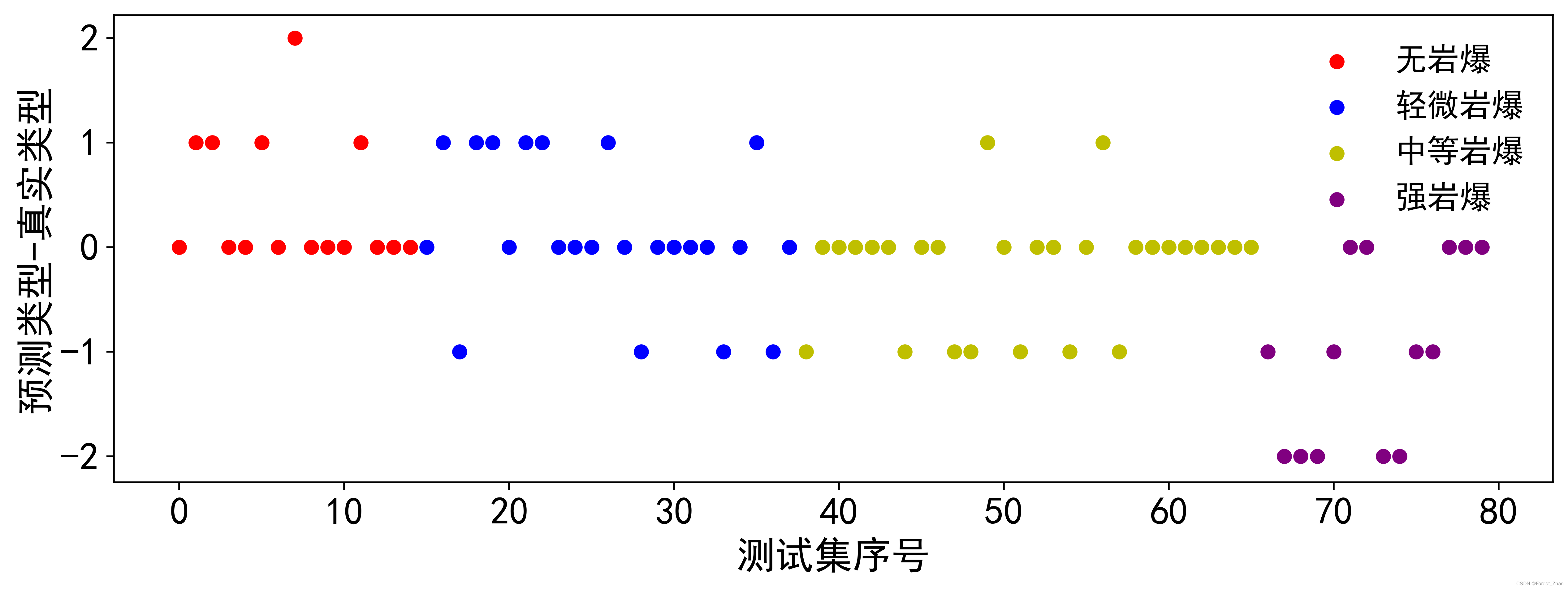
图6 SVM预测结果

图7 SMOTE-DT预测结果

代码：预测结果

plt.figure(figsize=(12,4))

real_value_1 = []
predict_value_1 = []
real_value_2 = []
predict_value_2 = []
real_value_3 = []
predict_value_3 = []
real_value_4 = []
predict_value_4 = []

for eachX,eachY in zip(clf.predict(test_data[["sigma_theta","sigma_c","sigma_t","SCF","B1","B2","Wet"]]),test_data["y"]):
    if eachY == 1:
        real_value_1.append(eachY)
        predict_value_1.append(eachX)
    if eachY == 2:
        real_value_2.append(eachY)
        predict_value_2.append(eachX)
    if eachY == 3:
        real_value_3.append(eachY)
        predict_value_3.append(eachX)
    if eachY == 4:
        real_value_4.append(eachY)
        predict_value_4.append(eachX)
    
error_value1 = np.array(real_value_1) - np.array(predict_value_1)
error_value2 = np.array(real_value_2) - np.array(predict_value_2)
error_value3 = np.array(real_value_3) - np.array(predict_value_3)
error_value4 = np.array(real_value_4) - np.array(predict_value_4)


# plt.scatter(list(range(len(real_value))),real_value,label="真实类别")
# plt.scatter(list(range(len(predict_value))),predict_value,label="预测类别")
plt.scatter(list(range(len(error_value1))),-error_value1,c="r",label="无岩爆")
plt.scatter(list(range(len(error_value1),len(error_value1)+len(error_value2))),-error_value2,c="b",label="轻微岩爆")
plt.scatter(list(range(len(error_value1)+len(error_value2),len(error_value1)+len(error_value2)+len(error_value3))),-error_value3,c="y",label="中等岩爆")
plt.scatter(list(range(len(error_value1)+len(error_value2)+len(error_value3),len(error_value1)+len(error_value2)+len(error_value3)+len(error_value4))),-error_value4,c="purple",label="强岩爆")


plt.ylabel("预测类型-真实类型",fontsize=18)
plt.xlabel("测试集序号",fontsize=18)
plt.xticks(fontsize=18)
plt.yticks([-2,-1,0,1,2,3],fontsize=18)
plt.legend(fontsize=15,frameon=False)
plt.savefig("决策树预测结果",dpi=500,bbox_inches = 'tight')

（3）不同类别岩爆分类性能

为获取3种机器模型对不同类别岩爆样本的分类性能，采用精确率、召回率、F1值、宏平均与微平均指标进行计算，3种机器学习算法性能评价如表7所示。从宏平均与微平均指标来看，SMOTE-DT模型相较于KNN与SVM模型对不同类别岩爆样本的分类能力较强，KNN模型次之，SVM模型表现最差。

从3种算法精确率、召回率与F1的性能指标（图8）可以看出，SVM模型在强岩爆类型的召回率低于50%，说明被SVM模型预测为强岩爆类型的测试集中有50%以上实际并非强岩爆类型，模型对于强岩爆类型的预测十分不可靠。SMOTE-DT模型在四种岩爆类型上的分类性能均优于KNN与SVM模型，同时SMOTE-DT模型对于四种岩爆类型的F1值均大于0.7，分类性能稳定可靠。

表7 3种机器学习算法的性能评价

类别	评估指标	KNN	SVM	SMOTE-DT
N	P	0.71	0.77	0.75
	R	0.67	0.67	0.80
	F1	0.69	0.71	0.77
L	P	0.63	0.48	0.69
	R	0.65	0.61	0.78
	F1	0.64	0.54	0.73
M	P	0.71	0.62	0.84
	R	0.71	0.64	0.75
	F1	0.71	0.63	0.79
S	P	0.79	0.67	0.85
	R	0.79	0.43	0.79
	F1	0.79	0.52	0.81
宏平均	P_macro	0.71	0.63	0.78
	R_macro	0.70	0.59	0.78
	F1_macro	0.71	0.60	0.78
微平均	P_micro	0.70	0.60	0.78
	R_micro	0.70	0.60	0.78
	F1_micro	0.70	0.60	0.78

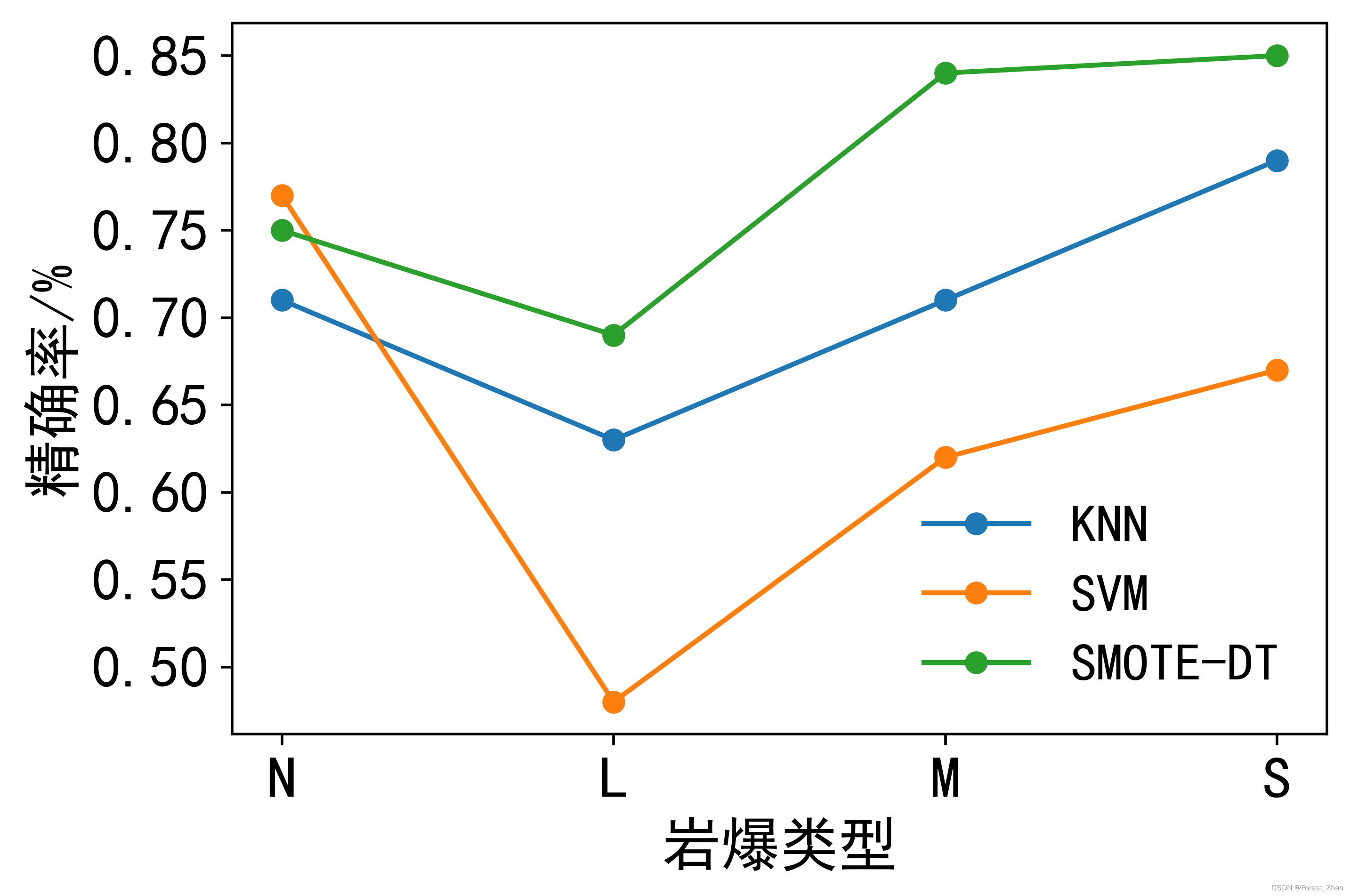图8 3种算法分类性能指标图

plt.figure(figsize=(6,4))

knn_p = [0.71,0.63,0.71,0.79]
knn_r = [0.67,0.65,0.71,0.79]
knn_f = [0.69,0.64,0.71,0.79]

svm_p = [0.77,0.48,0.62,0.67]
svm_r = [0.67,0.61,0.64,0.43]
svm_f = [0.71,0.54,0.63,0.52]

dt_p = [0.61,0.5,0.69,0.83]
dt_r = [0.73,0.52,0.64,0.71]
dt_f = [0.67,0.51,0.67,0.77]

plt.plot(["N","L","M","S"],knn_p,label="KNN",marker="o")
plt.plot(["N","L","M","S"],svm_p,label="SVM",marker="o")
plt.plot(["N","L","M","S"],dt_p,label="DT",marker="o")
plt.legend(fontsize=15)
plt.savefig("P精确率",dpi=500,bbox_inches = 'tight')
plt.show()

plt.plot(["N","L","M","S"],knn_r,label="KNN",marker="o")
plt.plot(["N","L","M","S"],svm_r,label="SVM",marker="o")
plt.plot(["N","L","M","S"],dt_r,label="DT",marker="o")
plt.legend(fontsize=15)
plt.savefig("R召回率",dpi=500,bbox_inches = 'tight')
plt.show()

plt.figure(figsize=(12,4))

plt.plot(["N","L","M","S"],knn_f,label="KNN",marker="o")
plt.plot(["N","L","M","S"],svm_f,label="SVM",marker="o")
plt.plot(["N","L","M","S"],dt_f,label="DT",marker="o")
plt.legend(fontsize=15)
plt.savefig("F1",dpi=500,bbox_inches = 'tight')
plt.show()