目录
- 一、选择填空判断题
- 题1
- 题2
- 题3
- 题4
- 题5
- 题6
- 题7
- 题8
- 题9
- 二、应用题
- 题10(遍历序列)
- 题11(存储结构)
- 题12 13(二叉树/树、森林之间的转换)
- 题14(线索二叉树)
一、选择填空判断题
题1
1、设高度为h的二叉树上只有度为0和度为2的结点,则该二叉树中所包含的结点数至少为(),最多为()。
A、h ;2h-1
B、2h-1 ; 2h-1
C、2h+1; 2h-1-1
D、h+1;2h-1
解析:(B)
最少的情况下,除了根结点该层为1个结点以外,其余h-1层都有2个结点,得2(h-1),即2(h-1)+1=2h-1。
最多的情况下,除了最后一层度为0,其余结点都是度为2的结点,即 2h-1个。
题2
2、一棵有124个叶结点的完全二叉树,最多有( )个结点。
A、247
B、248
C、249
D、250
解析:(B)
由于n0=n2+1,且N=n0+n1+n2,度为0和度为1的结点相差为1,所以完全二叉树中度为1的结点n1只可能是0或1,即当总结点数为偶数时n1=1,为奇数时n0=0。
本题中,n0=124,可得n2=123,由于是考虑最多结点数,即n1=1,所以N=124+123+1=248。
题3
3、若一棵二叉树有126个结点,在第7层(根结点在第1层)至多有()个结点。
A、32
B、64
C、63
D、不存在第7层
解析:(C)
考虑第1层到第6层结点都是满的情况,即第1层到第6层结点的结点数量为1+2+4+8+16+32=63个。第7层最多可有64个结点,由于二叉树有126个结点,即第7层还有126-63=63个结点。
题4
4 、一棵有n个结点的二叉树采用二次链表存储结点,其中非空指针数为(),空指针数为()。
A、n+1;n-1
B、n;n-1
C、n-1;n+1
D、2n;2n-1
解析:(A)
n个结点的数有n-1条分支,每个分支对应一个指针,所以非空指针数为n-1;另外,由于每个结点中包含2个指针域(左指针域lchild、右指针域rchild),总指针域数量减去非空指针数即为空指针数,2n-(n-1)=n+1。
题5
5、在二叉树的前序序列、中序序列和后序序列中,所有叶子结点的先后顺序是()。
A、都不相同
B、完全相同
C、前序序列和中序序列相同,与后序序列不同
D、中序序列和后序序列相同,与前序序列不同
解析:(B)
三种遍历方式中,访问左右子树的顺序是相同的,只是访问根结点的先后顺序不同,故所有叶子结点的先后顺序是相同的。
题6
6、线索二叉树是一种()结构。
A、逻辑
B、逻辑和存储
C、物理
D、线性
解析:(C)
二叉树是一种逻辑结构,而线索二叉树是加上线索的链表结构,是一种物理结构。
题7
7、在有n个叶子结点的哈夫曼树中,非叶子结点的总数是();若该哈夫曼树有215个结点,对其进行哈夫曼编码,可以得到()个不同的码字。
A、n-1;108
B、n;107
C、2n-1;214
D、2n;215
解析:(A)
哈夫曼树中只有度为0和2的结点,由n0=n2+1,可得:非叶子结点的总数为n-1。
结点总数N=n0+n2,且n0=n2+1,N=215代入可得,n0=108。
题8
8、找出下列条件的二叉树:
A、先序遍历序列与后序遍历序列相同,为()
B、中序遍历序列与后序遍历序列相同,为()
C、先序遍历序列与中序遍历序列相同,为()
D、中序遍历序列与层次遍历序列相同,为()
解析:
A、空树或只有根结点的二叉树;
B、空树或任一结点至多只有左子树;
C、空树或任一结点至多只有右子树;
D、空树或任一结点至多只有右子树。
题9
9、(判断)哈夫曼编码树中,两个频率相同的字符具有相同的哈夫曼编码。
解析:(×)
不会有相同的哈夫曼编码,除非它们的字符相同,从而得到的哈夫曼编码也相同。
二、应用题
题10(遍历序列)
题型:通过已知树的遍历序列,求其他遍历序列
10、某二叉树的中序遍历序列为ABCDEFG,后序遍历序列为BDCAFGE,求其先序遍历序列。
解:可知,二叉树的先、中、后序遍历序列以及层次遍历序列的遍历顺序如下:
| 遍历名称 | 遍历规则 |
|---|---|
| 先序遍历序列 | 根 > 左 > 右 |
| 中序遍历序列 | 左 > 根 > 右 |
| 后序遍历序列 | 左 > 右 > 根 |
| 层次遍历序列 | 左 > 右 |
首先,通过所给的两个序列恢复二叉树,后序遍历序列为BDCAFGE,所以该序列的最后一个元素“E”为二叉树的根结点,从而可得到:

继续对左子树和右子树的中序遍历和后序遍历进行拆分,先看E的左子树,由后序序列可知左子树中A为根结点,且由后序序列可知A无左子树,右子树为BCD;同理,E的右子树中,右子树中G为根结点,但是无法判断F为其左子树还是右子树,所以看中序遍历序列中,G的左边是F,由中序遍历规则,所以F为G的左子树,同时G无右子树,如下:
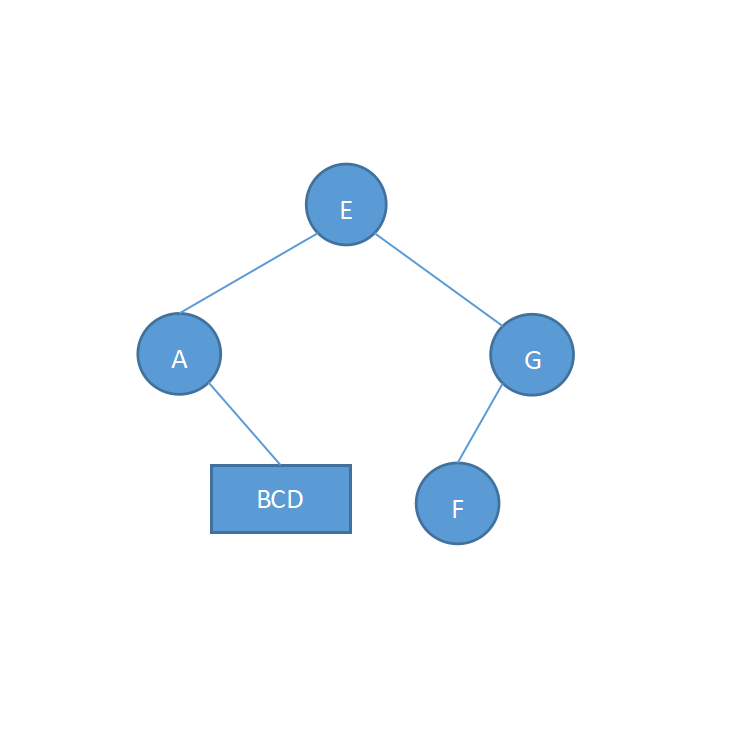
同上,可得C为根结点A的右子树,C的左子树为B,右子树为D,如下既是一棵完整的二叉树:
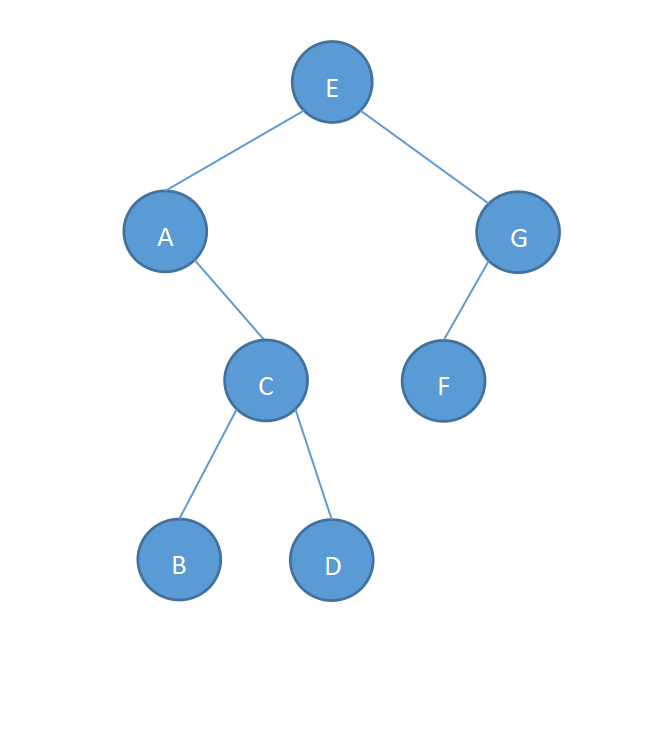
故可得其先序遍历序列:EACBDGF。
题11(存储结构)
题型:根据树的存储结构,画出二叉树
11、下图是一个二叉树的顺序存储结构,其中空白表示该结点不存在,画出该二叉树,并求出该二叉树的中序序列和后序序列。

解:按完全二叉树存储,其中空白的为空,如下:
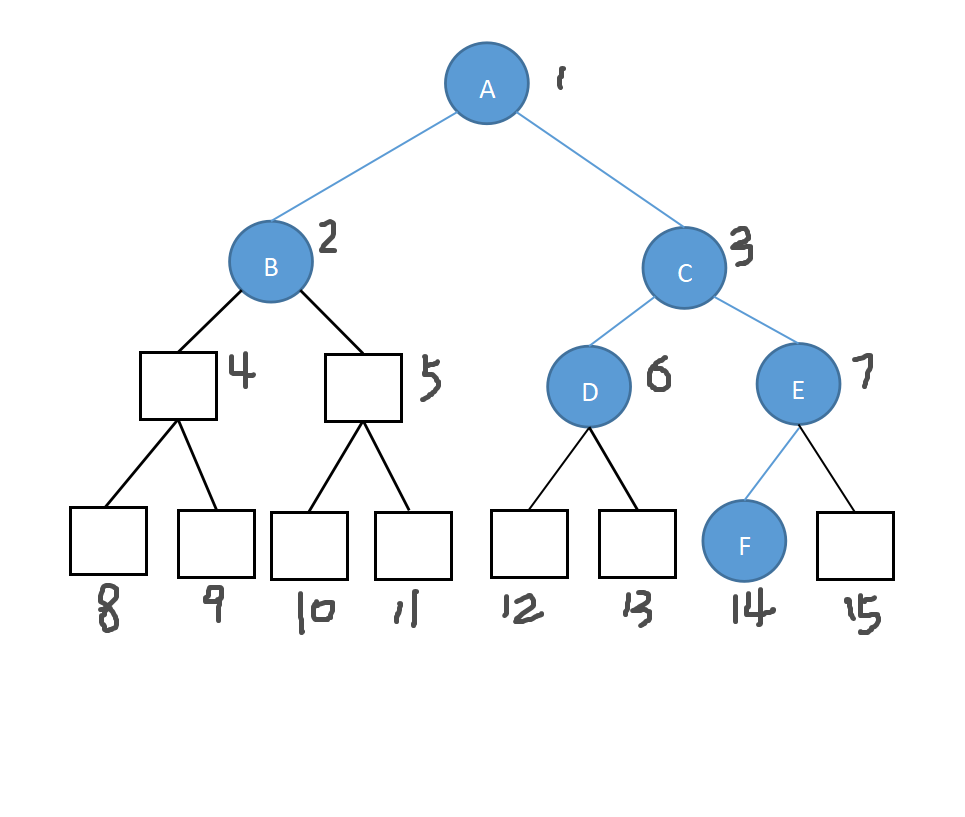
注:其中黑色标注只是为了更清楚展示该二叉树,二叉树建议只留蓝色部分即可。
中序序列:BADCFE;后序序列:BDFECA。
题12 13(二叉树/树、森林之间的转换)
题型一:根据所给二叉树,将其转换为树
12、将以下这棵二叉树转换为树。
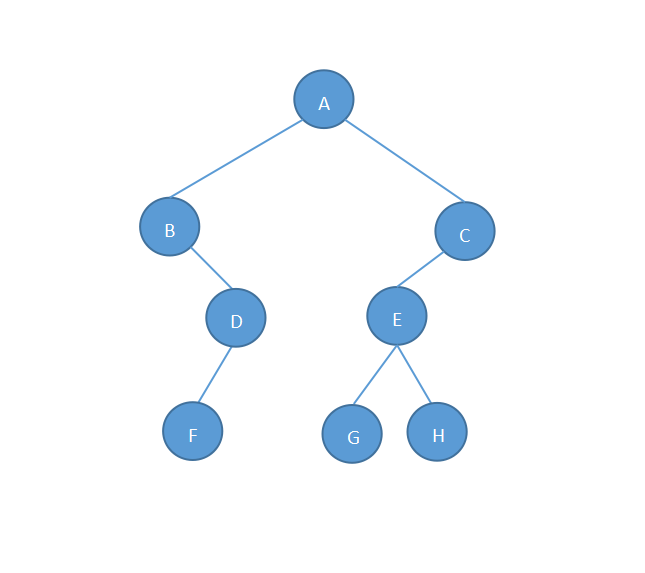
解:第一步,旋转。将该二叉树中除了根结点左右子树的所有结点向右旋转45°,如下:
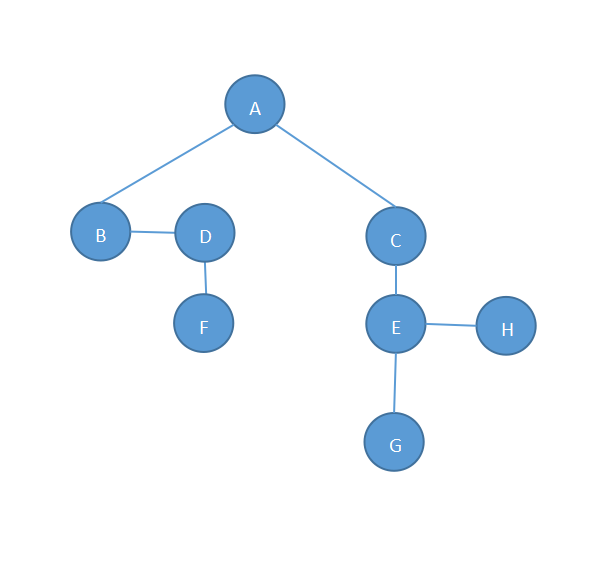
第二步,连线。若某结点的左孩子有右子树,则右子树与该结点相连,A结点的左孩子B有右子树D,所以将A与D相连;C结点的左孩子E有右子树H,所以将C与H相连,如下:
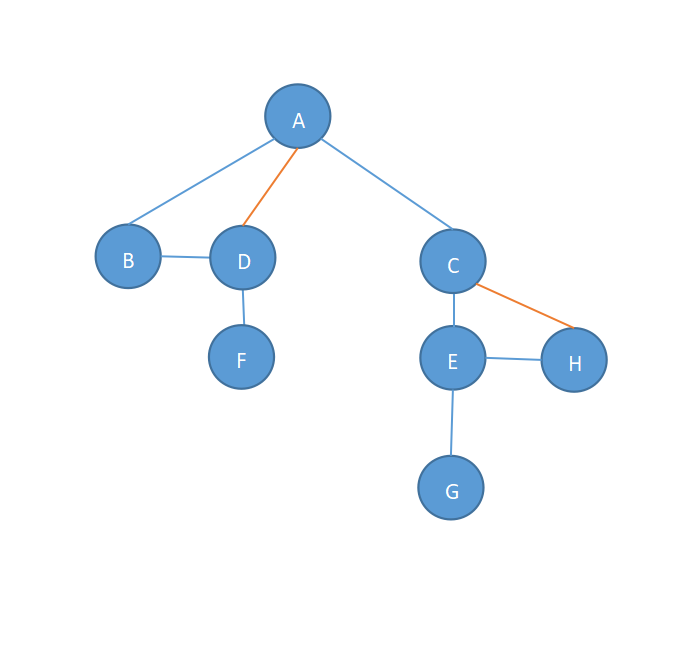
第三步,断线。删除除根结点外各结点右子树的右分支与其父结点连线,如下:
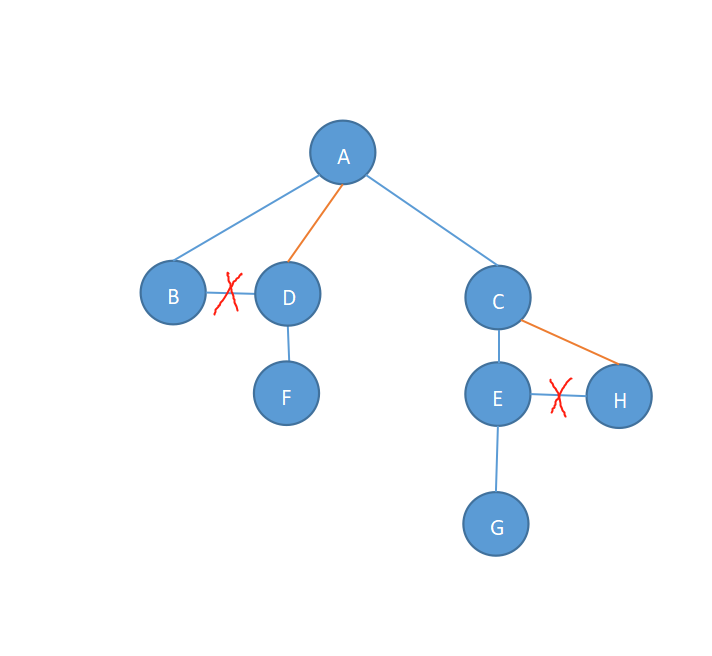
即可得到二叉树转换而来的树:

题型二:根据所给森林,将其转换为二叉树
13、已知下面由三棵树组成的森林,将其转换为二叉树。
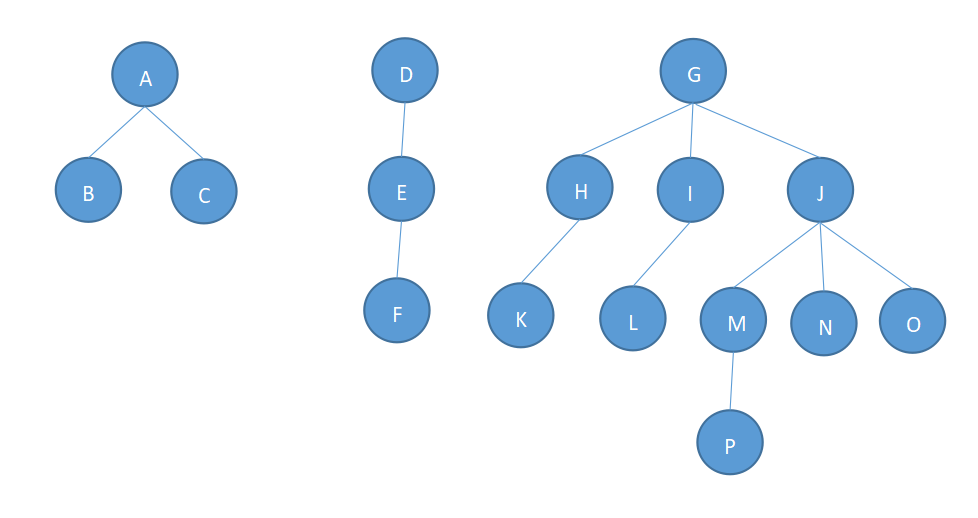
解:第一步,连线。首先将所有结点的兄弟结点相连,另外各树的根结点也相连,如下:
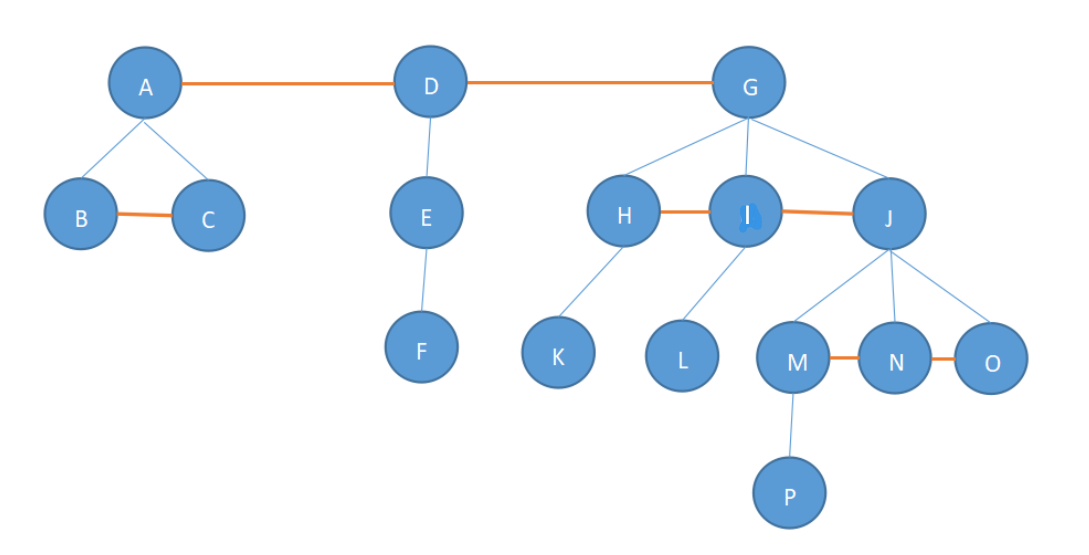
第二步,断线。只保留所有结点的最左边子女,而其他结点断开,如下:
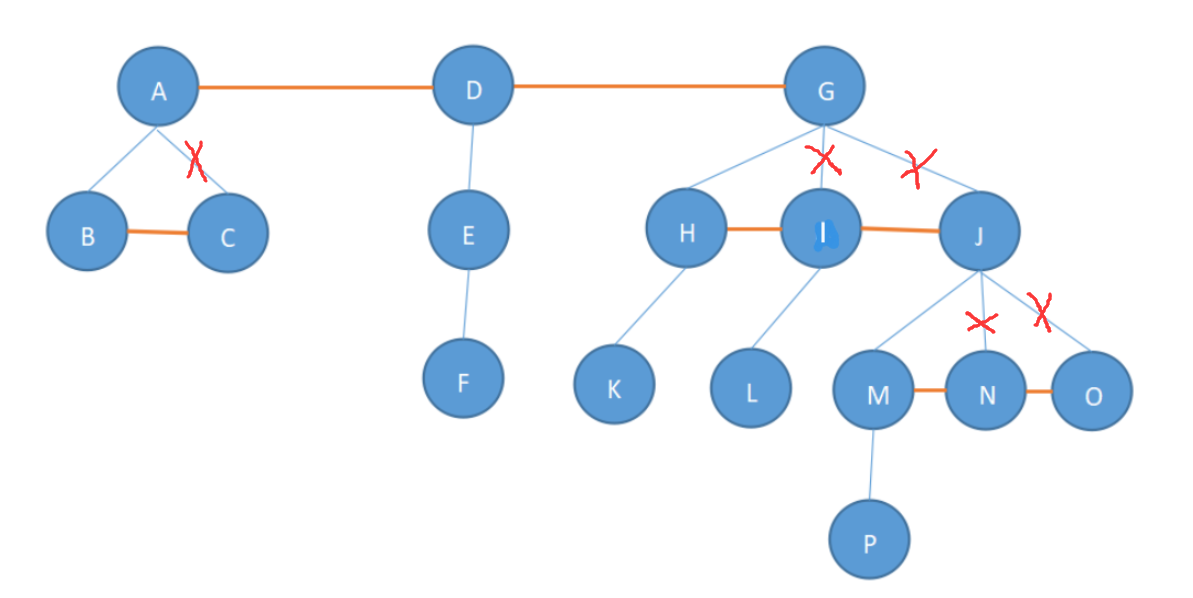
断开后:
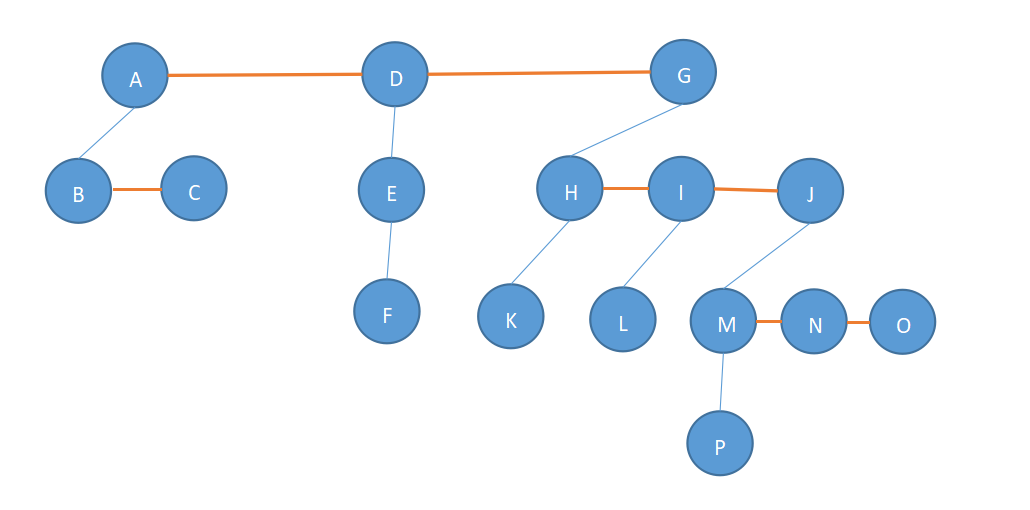
第三步,旋转。以第一棵树的根结点为轴心,顺时针旋转45°,如下:
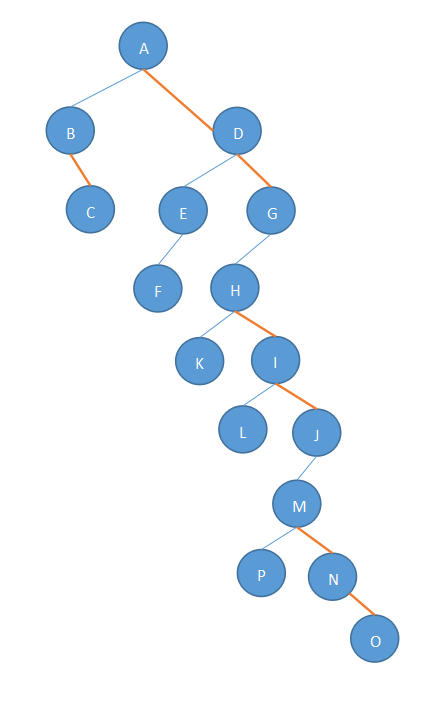
题14(线索二叉树)
题型:根据所给二叉树,画出该二叉树的线索二叉树
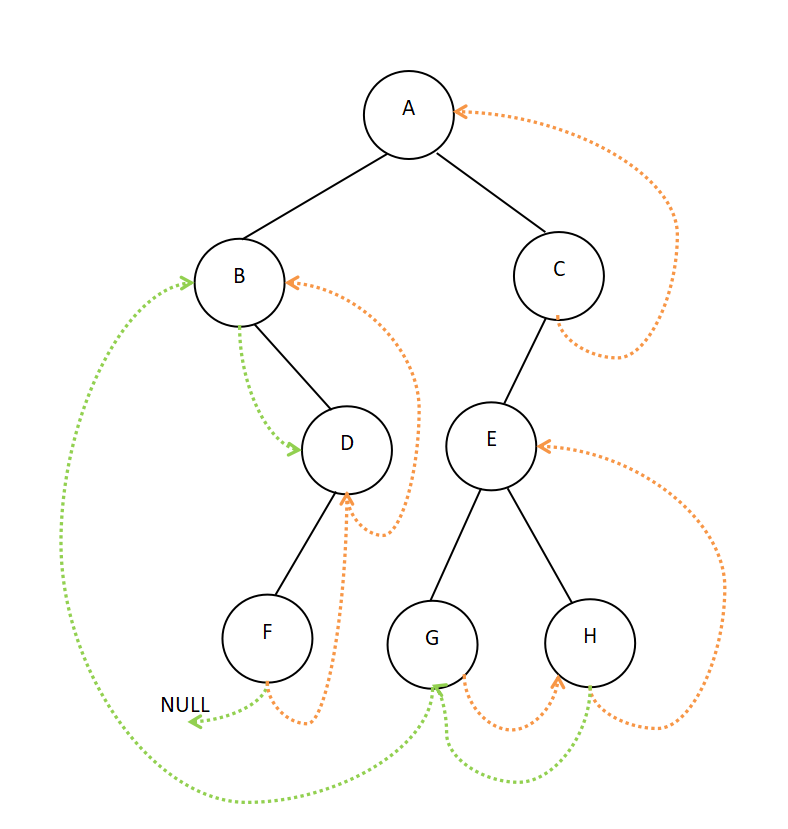
14、设一棵二叉树的先序、中序遍历序列分别为ABDFCEGH和BFDAGEHC,求这棵二叉树的后序线索树。
解:首先,求出该二叉树,可以得到:
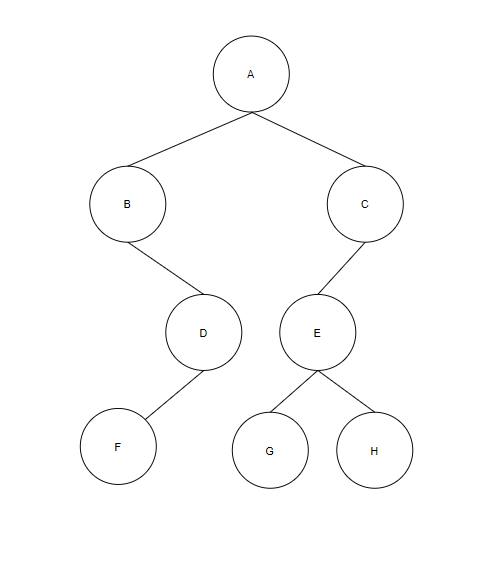
第一步,求出要画的相应线索二叉树的先/中后序遍历序列。可得到其后序遍历序列是FDBGHECA。
第二步,画线索(针对二叉树中缺少左、右孩子的结点)。若该结点无左孩子,则线索指向相应线索二叉树的先/中/后序遍历序列的前驱,若无前驱则指向NULL;若该结点无右孩子,则线索指向相应线索二叉树的先/中/后序遍历序列的后继,若无后继则指向NULL。
例如,结点D无右孩子,在后序遍历序列中结点D的后继是B,所以指向B;结点F无左孩子,在后序遍历序列中结点F无前驱结点,所以指向NULL;结点H无左孩子和右孩子,在后序遍历序列中结点H的前驱是G,后驱是E,所以分别指向G和E,如下: