欢迎关注我的CSDN：https://spike.blog.csdn.net/
本文地址：https://blog.csdn.net/caroline_wendy/article/details/131097165

马尔可夫决策过程（Markov Decision Process，MDP）和马尔可夫奖励过程（Markov Reward Process，MRP）之间存在一种转换关系。下面我将详细介绍这个转换过程。

马尔可夫决策过程（MDP）是一种数学模型，用于描述一个决策过程中的随机性和不确定性。MDP由5个元素组成：状态集合（S），动作集合（A），状态转移概率函数（P），奖励函数（R），以及折扣因子（γ）。

然而，马尔可夫决策过程并不直接包含奖励信息，而是通过引入马尔可夫奖励过程（MRP）来处理奖励。马尔可夫奖励过程是马尔可夫决策过程的一个子集，不包含动作集合和策略。

下面是将MDP转换为MRP的步骤：

1. 状态集合（S）和动作集合（A）不变：在转换过程中，状态集合和动作集合保持不变。
2. 状态转移概率函数（P）：对于每个状态 s 和动作 a 的组合，计算该组合下的状态转移概率。这可以通过对所有可能的下一个状态 s’ 的概率进行求和来完成。即对于每个 s 和 a，计算 P(s’|s, a)。
3. 奖励函数（R）：为每个状态 s 和动作 a 的组合计算奖励。这可以通过对所有可能的下一个状态 s’ 的奖励进行加权平均来完成。即对于每个 s 和 a，计算 R(s, a, s’) = Σ P(s’|s, a) * R(s, a, s’)。
4. 折扣因子（γ）：将原始MDP中的折扣因子 γ 保持不变。

经过这个转换过程，我们从MDP转换为了MRP，即马尔可夫奖励过程。在MRP中，我们不再考虑动作和策略，而是仅关注状态转移概率和奖励函数。这使得我们可以更加专注于对奖励过程的建模和分析。

需要注意的是，从MRP转换回MDP是不可能的，因为MRP中没有动作和策略的概念。因此，从MDP到MRP的转换是可逆的，但反过来是不可逆的。

---

马尔可夫决策过程（Markov Decision Process，MDP），在马尔可夫奖励过程（Markov Reward Process，MRP）的基础上，引入动作（Action），即 $<\mathcal{S},\mathcal{A},\mathcal{P},r,\gamma >$。

即引入动作集合 $\mathcal{A}$，奖励reward由 $r(s)$ 转换为 $r(s,a)$ ，状态转移概率由 $\mathcal{P}(s^{\prime }|s)$ 转换为 $\mathcal{P}(s^{\prime }|s,a)$，都增加动作 $a$。同时，引入策略 $\pi$ 的概念。

策略 $\pi$ 包括2类，确定性策略（Deterministic Policy）和随机性策略（Stochastic Policy）。确定性策略即状态转移链，即一个状态确定到另一个状态，也可以理解为概率为1，其他都是0。随机性策略即状态转移概率，即状态 $s_1$ 到 $[s_1,s_2,s_3,...]$的概率，更为普适。

马尔可夫决策过程（ $<\mathcal{S},\mathcal{A},\mathcal{P},r,\gamma >$） + 策略 $\pi$ = 马尔可夫奖励过程（$<\mathcal{S},\mathcal{P},r,\gamma >$）

MRP的状态转移概率矩阵，转换公式如下：
$$P(s^{\prime }|s)=\sum _{a\in A}\pi (a|s)P(s^{\prime }|s,a)$$
MRP的状态奖励列表，转换公式如下：
$$r^{\prime }(s)=\sum _{a\in A}\pi (a|s)r(s,a)$$
这样，就可以使用 MRP 的贝尔曼方程（Bellman Equation），计算 MDP 的在策略 $\pi$ 状态价值 $V^{\pi }(s^{\prime })$，贝尔曼方程（Bellman Equation）如下：

$$\begin{gathered} \mathcal{V}=\mathcal{R}+\gamma \mathcal{P}\mathcal{V} \\ \mathcal{V}=(\mathcal{I}-\gamma \mathcal{P}{)}^{-1}\mathcal{R} \end{gathered}$$

有了状态价值 $V^{\pi }(s^{\prime })$，即可以计算动作价值 $Q^{\pi }(s,a)$，即在状态 $s$ 时，执行 $a$ 动作的价值，在某个状态，尽量使用价值最高的动作，类似自动驾驶中，碰见某类情况，使用最优的动作进行处理，因为动作价值最高。

$$Q^{\pi }(s,a)=r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })$$

示例如下：

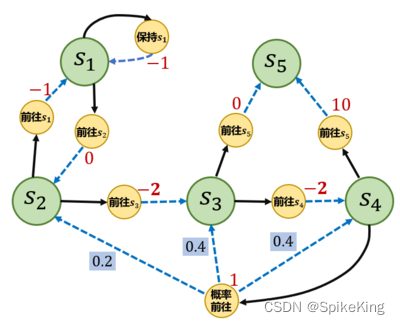
源码如下：

#!/usr/bin/env python
# -- coding: utf-8 --
"""
Copyright (c) 2022. All rights reserved.
Created by C. L. Wang on 2023/6/7
"""

import numpy as np

def compute(P, rewards, gamma, states_num):
  """
  利用 贝尔曼方程 解析状态价值
  """
  rewards = np.array(rewards).reshape((-1, 1))  # 转换成列向量
  value = np.dot(np.linalg.inv(np.eye(states_num, states_num) - gamma * P), rewards)
  return value


def main():
    S = ["s1", "s2", "s3", "s4", "s5"]  # 状态集合
    A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]  # 动作集合
    # 状态转移函数
    P = {
        "s1-保持s1-s1": 1.0,
        "s1-前往s2-s2": 1.0,
        "s2-前往s1-s1": 1.0,
        "s2-前往s3-s3": 1.0,
        "s3-前往s4-s4": 1.0,
        "s3-前往s5-s5": 1.0,
        "s4-前往s5-s5": 1.0,
        "s4-概率前往-s2": 0.2,
        "s4-概率前往-s3": 0.4,
        "s4-概率前往-s4": 0.4,
    }
    # 奖励函数
    R = {
        "s1-保持s1": -1,
        "s1-前往s2": 0,
        "s2-前往s1": -1,
        "s2-前往s3": -2,
        "s3-前往s4": -2,
        "s3-前往s5": 0,
        "s4-前往s5": 10,
        "s4-概率前往": 1,
    }
    gamma = 0.5  # 折扣因子
    MDP = (S, A, P, R, gamma)

    # 策略1,随机策略
    Pi_1 = {
        "s1-保持s1": 0.5,
        "s1-前往s2": 0.5,
        "s2-前往s1": 0.5,
        "s2-前往s3": 0.5,
        "s3-前往s4": 0.5,
        "s3-前往s5": 0.5,
        "s4-前往s5": 0.5,
        "s4-概率前往": 0.5,
    }
    # 策略2
    Pi_2 = {
        "s1-保持s1": 0.6,
        "s1-前往s2": 0.4,
        "s2-前往s1": 0.3,
        "s2-前往s3": 0.7,
        "s3-前往s4": 0.5,
        "s3-前往s5": 0.5,
        "s4-前往s5": 0.1,
        "s4-概率前往": 0.9,
    }

    # 把输入的两个字符串通过“-”连接,便于使用上述定义的P、R变量
    def join(str1, str2):
        return str1 + '-' + str2

    # 策略1,随机策略
    # 第1行: "s1-s1": 0.5, "s1-s2": 0.5
    # 第2行: "s2-s1": 0.5, "s2-s3": 0.5
    # 第3行: "s3-s4": 0.5, "s3-s5": 0.5
    # 第4行："s4-s5": 0.5, "s4-概率前往": 0.5 * ["s4-概率前往-s2": 0.2, "s4-概率前往-s3": 0.4, "s4-概率前往-s4": 0.4]
    # 第5行：终点
    P_from_mdp_to_mrp = [
        [0.5, 0.5, 0.0, 0.0, 0.0],
        [0.5, 0.0, 0.5, 0.0, 0.0],
        [0.0, 0.0, 0.0, 0.5, 0.5],
        [0.0, 0.1, 0.2, 0.2, 0.5],
        [0.0, 0.0, 0.0, 0.0, 1.0],
    ]
    P_from_mdp_to_mrp = np.array(P_from_mdp_to_mrp)

    # R奖励:
    # 第1个值: 0.5 * -1 + 0.5 * 0 = -0.5
    # 第2个值：0.5 * -1 + 0.5 * -2 = -1.5
    # 第3个值：0.5 * -2 + 0.5 * 0 = -1.0
    # 第4个值：0.5 * 10 + 1 * 0.5 = 5.5
    # 第5个值：final = 0
    R_from_mdp_to_mrp = [-0.5, -1.5, -1.0, 5.5, 0]
    V = compute(P_from_mdp_to_mrp, R_from_mdp_to_mrp, gamma, 5)
    print("MDP中每个状态价值分别为\n", V)


if __name__ == '__main__':
    main()

输出 $s_1\sim s_6$ 的状态价值 $V^{\pi }(s^{\prime })$ 如下：

 [[-1.22555411]
 [-1.67666232]
 [ 0.51890482]
 [ 6.0756193 ]
 [ 0.        ]]

状态动作价值 $Q^{\pi }(s_4,概率前往)$ 是：
$$\begin{gathered} Q^{\pi }(s,a)=r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime }) \\ 2.152=1+0.5\ast [0.2\ast (-1.68)+0.4\ast 0.52+0.4\ast 6.08] \end{gathered}$$