一、有符号整型的编码方式

1. 真值

把用"+"、"-"表示符号，数值部分用绝对值的编码的表示方式称为真值。

如+3用4bit真值表示为+0011，-1用真值表示为-0011。

2. 原码

符号位为0表示正数，符号位为1表示负数，数值位为真值的绝对值。

以8bit数值为例，最高1位位符号位，则

 1 的原码表示为 +000 0001 => 0,000 0001

-1 的原码表示为  -000 0001 => 1,000 0001

3. 反码

x>=0时，反码与原码相同；x<0时，反码为|x|的按位取反。

 1 的反码表示为 +000 0001 => 0,000 0001

-1 的反码表示为  -000 0001 => 1,111 1110

4. 补码

x>=0时，移码与原码相同；x<0时，补码为|x|的按位取反再加1。

 1 的补码表示为 +000 0001 => 0,000 0001

-1 的补码表示为  -000 0001 => 1,111 1110 + 1 => 1,111 1111

5. 移码

 对于一个nbit的整形数值，如果它表示有符号数，则它的表示范围为；如果它表示无符号数，则它的表示范围为。

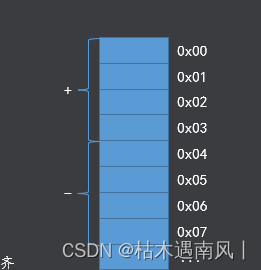
可以看出，如果给有符号数的表示范围整体加上作为偏移值，则刚好符合表示无符号数的表示范围。这种类似前移的操作得到的编码称为移码。

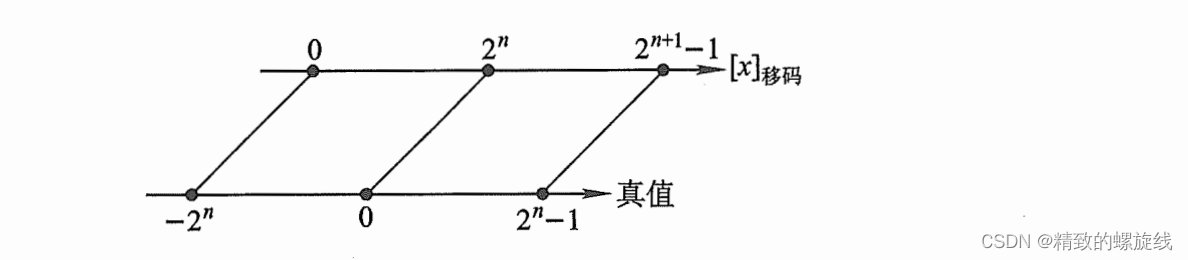
 注：上面这张图是我从别的地方抄来的，它表示一个(n+1)bit的移码的表示范围。

 1 的移码表示为 +000 0001 => 1,000 0000 +000 0001 => 1,000 0001

-1 的移码表示为 -000 0001 => 1,000 0000  -000 0001 => 0,111 1111

因此，对于一个nbit的移码，有如下规律

1. 通过观察可以发现，移码刚好与补码的数值位完全相同，符号位相反。

2.  移码保留了数据原有的大小顺序，即移码大则真值大，移码小则真值小。

3.  移码全为0时，对应真值也是最小值，即；移码全为1时，对应真值也取最大值，即。

二、浮点数的编码方式

1. 非规格化浮点数

浮点数由阶码j和尾数m构成，一个基数为r的浮点数表示为

m为尾数，是一个小数，通常为有符号的定点小数，一般使用原码表示，有一位符号位。

j为阶码，即指数，是一个有符号整数，通常用移码表示，有一位符号位。

r为基数，可以取2、8、10等任意数值，但通常取2。

以二进制浮点数即2.3125为例，它可以写成各种不同的表示形式

因此也可以得知使用非规格化浮点数表示浮点数的方法并不唯一。

2. 规格化浮点数

为了让浮点数有统一的表现形式，也为了使有限字长的浮点数尽可能表示更多的有效位数，因此有了规格化的浮点数表示方法。

通过左右移动位数的小数点，使得尾数为0.1xxxx的形式，即要求，然后再转为浮点数的存储形式。

例如2.3125，规格化后的写法为，如果用一个含1位符号位、用移码表示的5bit阶码和含1位符号位、用原码表示的11bit尾数来表示该数值，则有

 

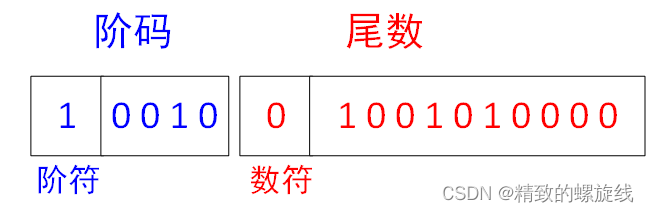
二、IEEE 754标准下的浮点数表示方法

以float型浮点数为例，该类型数据占4字节，其结构如下。

 则该浮点数的取值为

最高位为1bit的数符S，S为0表示该浮点数是正数，1表示负数。

8bit为阶码j，其中包含一位的阶符。阶码用移码表示，IEEE规定阶码全为0时表示0，阶码全为1时表示无穷大。因此，这个移码的偏移值不是而是。因此，移码可以表示的范围是[-126, 127]。

23bit为尾数m，没有符号位。IEEE 754是规格化的浮点数，要求必须左右移动小数点至尾数为1.xxxxx的形式，且存储时省略最高位的1。因此，m全为0时表示1.000...00；m全为1时表示1.111...11。因此尾数m的表示范围为[1, 2)。

因此，float型浮点数可以表示的最大正数为

最小正数为

最大负数和最小负数同理。

以数值178.125为例，它用二进制表示为10110010.001，规格化后为。

因此，尾数为01100100010000000000000。阶码为00000111+01111111=10000110。

所以该数值的float型编码结果为