自适应滤波有很多种方式，也很实用

一、自适应滤波基本思想

函数模型
$$\{\begin{array}{l}{\mathbf{X}}_k={\mathbf{\Phi }}_{k/k-1}{\mathbf{X}}_{k-1}+{\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\\ {\mathbf{Z}}_k={\mathbf{H}}_k{\mathbf{X}}_k+{\mathbf{V}}_k\end{array}$$
随机模型
$$\{\begin{array}{lc}\mathrm{E}\left[{\mathbf{W}}_k\right]={\mathbf{q}}_k,& \mathrm{E}\left[{\mathbf{W}}_k{\mathbf{W}}_j^{\mathrm{T}}\right]={\mathbf{Q}}_k{\delta }_{kj}\\ \mathrm{E}\left[{\mathbf{V}}_k\right]={\mathbf{r}}_k,& \mathrm{E}\left[{\mathbf{V}}_k{\mathbf{V}}_j^{\mathrm{T}}\right]={\mathbf{R}}_k{\delta }_{kj}\\ \mathrm{E}\left[{\mathbf{W}}_k{\mathbf{V}}_j^{\mathrm{T}}\right]=0& \end{array}$$
系统噪声和量测噪声都不是零均值，且噪声的均值和方差都未知，用标准Kalman滤波没法做。

基本原理：噪声参数不准会影响系统输出，利用输出边作状态估计边作噪声辨识，需要系统的可观测新比较强。

• 噪声均值均可等效于状态增广。把噪声分解成零均值部分和非零均值部分，非零均值的部分作为状态一并估计。所以对系统噪声和量测噪声的均值用自适应方法没有必要，真的未知又想估计它，就把它扩维增广为状态。
• 系统噪声方差难以自适应，代表系统的状态，一般来说系统比较稳定，做自适应比较难。
• 量测噪声方差相对容易自适应，代表仪器和环境的状态，有可能时好时坏，用自适应效果比较好。
• 应尽量减少噪声自适应参数的数目，可以只对容易变化的量测做自适应。

二、量测噪声方差阵自适应算法

新息和新息的方差
$$\begin{array}{l}{\tilde{\mathbf{Z}}}_{k/k-1}={\mathbf{Z}}_k-{\hat{\mathbf{Z}}}_{k/k-1}={\mathbf{H}}_k{\mathbf{X}}_k+{\mathbf{V}}_k-{\mathbf{H}}_k{\hat{\mathbf{X}}}_{k/k-1}={\mathbf{H}}_k{\tilde{\mathbf{X}}}_{k/k-1}+{\mathbf{V}}_k\\ \mathrm{E}\left[{\tilde{\mathbf{Z}}}_{k/k-1}{\tilde{\mathbf{Z}}}_{k/k-1}^{\mathrm{T}}\right]={\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}+{\mathbf{R}}_k\end{array}$$
想估计 $R$ ，就认为左边都已知，就是新息量测值的方差减去预测量测值方差
$${\mathbf{R}}_k=\mathrm{E}\left[{\tilde{\mathbf{Z}}}_{k/k-1}{\tilde{\mathbf{Z}}}_{k/k-1}^{\mathrm{T}}\right]-{\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}$$
这种的满足只是统计上整体的满足，不是说每一次测量都应该满足。

以估计房间的温度的例子来说：预测下一时刻的量测温度，再用温度计量测一下，只利用两个的值来确定量测噪声，仅仅只是一个样本；要得到方差，需要很多个房间，很多次测量算出来的才是 $R_k$，才得出统计结果。

实际做Kalman滤波研究的往往只有一个样本，用时间平均来算，多个时刻的数据得出 $R_k$ 。并且写成递推的形式如下：
$$\begin{array}{rl}{\hat{\mathbf{R}}}_k& =\frac{1}{k}\sum _{i=1}^k\left({\tilde{\mathbf{Z}}}_{i/i-1}{\tilde{\mathbf{Z}}}_{i/i-1}^{\mathrm{T}}-{\mathbf{H}}_i{\mathbf{P}}_{i/i-1}{\mathbf{H}}_i^{\mathrm{T}}\right)\\ & =\frac{1}{k}\left[\sum _{i=1}^{k-1}\left({\tilde{\mathbf{Z}}}_{i/i-1}{\tilde{\mathbf{Z}}}_{i/i-1}^{\mathrm{T}}-{\mathbf{H}}_i{\mathbf{P}}_{i/i-1}{\mathbf{H}}_i^{\mathrm{T}}\right)+\left({\tilde{\mathbf{Z}}}_{k/k-1}{\tilde{\mathbf{Z}}}_{k/k-1}^{\mathrm{T}}-{\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}\right)\right]\\ & =\left(1-\frac{1}{k}\right){\hat{\mathbf{R}}}_{k-1}+\frac{1}{k}\left({\tilde{\mathbf{Z}}}_{k/k-1}{\tilde{\mathbf{Z}}}_{k/k-1}^{\mathrm{T}}-{\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}\right)\end{array}$$
上式每个时刻的权重都相同，为等加权平均。统计很长时间后 $\frac{1}{k}$ 会趋于 $0$ ，时间越长，自适应的能力越差。

为避免此问题，可以把 $K$ 值限定，到了一定数目之后，就不让它再增加。如采用指数渐消记忆加权平均：
$${\hat{\mathbf{R}}}_k=\left(1-{\beta }_k\right){\hat{\mathbf{R}}}_{k-1}+{\beta }_k\left({\tilde{\mathbf{Z}}}_{k/k-1}{\tilde{\mathbf{Z}}}_{k/k-1}^{\mathrm{T}}-{\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}\right)$$
其中 ${\beta }_k=\frac{{\beta }_{k-1}}{{\beta }_{k-1}+b}{\beta }_0=1,{\beta }_{\infty }=1-b,0<b<1$ 称为渐消因子。$b$ 一般取的接近于 $1$，如 $0.9、0.99、0.999$

式子后半部分有矩阵相减，当实际噪声比较小时，容易出现量测方差负定，可改用“序贯标量量测+方差受限”自适应方法加以解决：

受限：比如GNSS精度 $1cm$，如果算出来量测方差是 $1nm$ 肯定有问题，可以设一个 $1cm$ 的限制

令 ${\rho }_k^{(i)}={\left({\tilde{Z}}_{k/k-1}^{(i)}\right)}^2-{\mathbf{H}}_k^{(i)}{\mathbf{P}}_{k/k-1}^{(i)}{\left({\mathbf{H}}_k^{(i)}\right)}^{\mathrm{T}}$ ，$R_{\text{max }}^{(i)},R_{\text{min }}^{(i)}$ 人为设置的方差上下限，有：
$${\hat{R}}_k^{(i)}=\{\begin{array}{cc}\left(1-{\beta }_k\right){\hat{R}}_{k-1}^{(i)}+{\beta }_k{R}_{\min }^{(i)}& {\rho }_k^{(i)}<R_{\min }^{(i)}\\ R_{\max }^{(i)}& {\rho }_k^{(i)}>R_{\max }^{(i)}\\ \left(1-{\beta }_k\right){\hat{R}}_{k-1}^{(i)}+{\beta }_k{\rho }_k^{(i)}& \text{ others }\end{array}$$
流程如下：

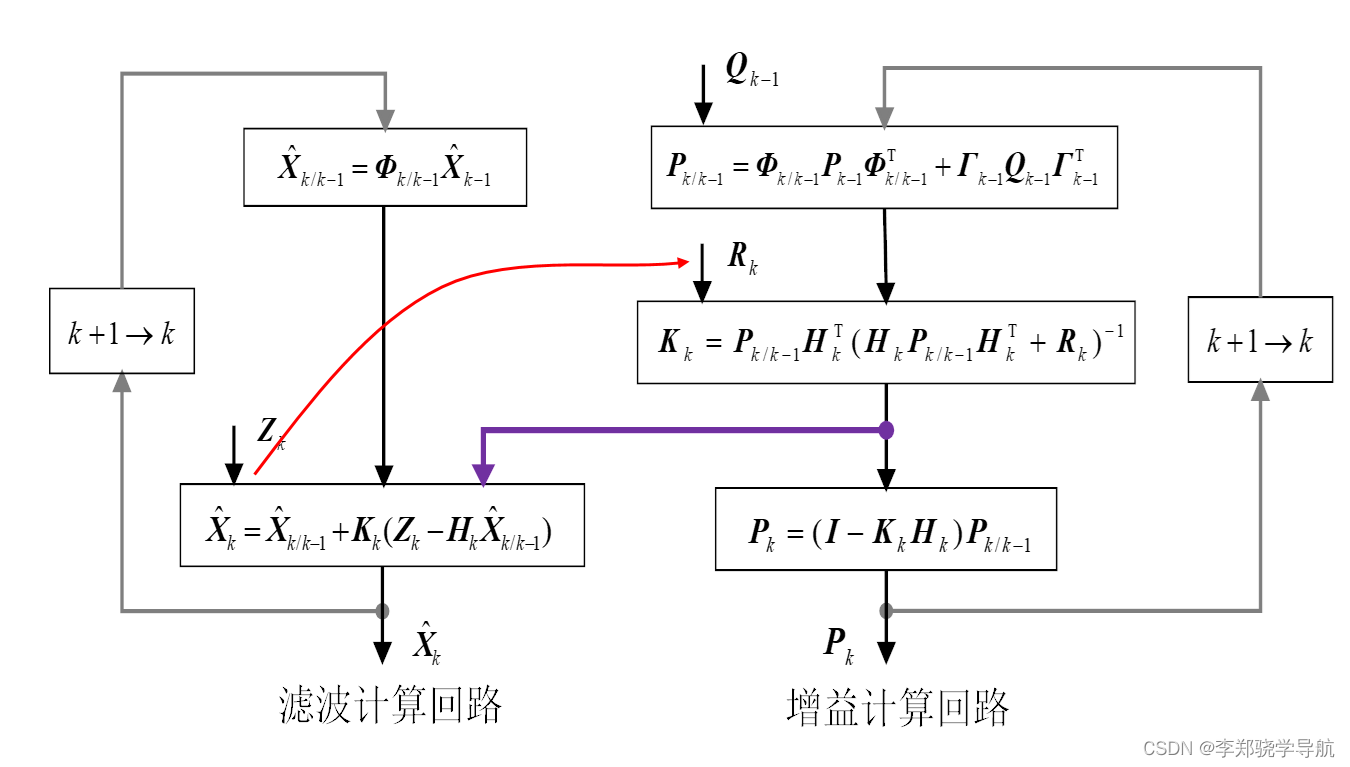
左边的系统对右边有作用，右边对左边也有作用，比较复杂，需要对其做稳定性分析和可控性分析很困难。判断工程上能不能用得做仿真。